next up previous
下一頁: Polynomials over the Integers 上一頁: 一些常見的 Rings 前一頁: The Ring of Integers


Ring of Polynomials over a Field

大家都知道有理係數的多項式有和整數很類似的性質, 就是所謂的餘式定理. 事實上這個定理對係數在一般的 field 的多項式也對的. 在這一節中我們將探討這種 polynomial ring. 大家會發異畯抴X乎是把上一節中整數的那一套理論完完整整的搬過來.

令 F 是一個 field. 我們考憧悕狾釭澈Y數在 F 的多項式

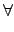f (x) = a0 + a1x + ... + an - 1xn - 1 + anxn,    ai $\displaystyle \in$ F  $\displaystyle \forall$ i = 0,..., n

所形成的集合 F[x]. 我們很自然給 F[x] 中的元素定義以下的加法和乘法: 若 f (x) = a0 + a1x ... + anxn 和 g(x) = b0 + b1x + ... + bmxm 是 F[x] 中的兩元素, 定 f (x) + g(x) = c0 + c1x + ... + crxr, 其中對所有的 i $ \in$ {1,..., r}, ci = ai + bi 且 r = max{m, n}. 另� 我們定 f (x) . g(x) = d0 + d1x + ... + dm + nxm + n, 其中對所有的 i $ \in$ {1,..., m + n},

di = a0 . bi + a1 . bi - 1 + ... + ai - 1 . b1 + ai . b0.

注意這裡, 當 j > n 時我們令 aj = 0 且 當 k > m 時我們令 bk = 0. 其實這就是我們熟知一般多項式的加法與乘法: 當相加時就是將同次項的係數相加; 相乘就是各項先展陲嶆A合併同次項.

經由一番的驗算我們可以得到 F[x] 是一個 commutative ring with 1, 這裡我們就略去驗算過竣F. 不過要強調一下 F[x] 這個 ring 的加法 identity 0 就是 0 多項式, 也就是各項係數都是 0 (這裡的 0 是 F 的 0) 的多項式. 而乘法的 identity 1 就是 1 這一個常數多項式, 也就是常數項為 1 (這裡的 1 是 F 的 1) 其他項係數都是 0. 通常我們稱 F[x] 為 the ring of polynomials in x over F.

當我們碰到一個新的 ring 時, 首先會問的是它的 zero divisor 和 unit 有哪些? 這裡由於我們處理的是 polynomial ring 有一個特別好用的工具來幫我們, 就是所謂的 degree.

Definition 7.2.1   若 f (x) = a0 + a1x + ... + anxn $ \in$ F[x] 且 an$ \ne$ 0, 則稱 f (x) 的 degree 為 n 記為 deg(f (x)) = n.

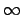注意雖然 0 多項式我們看成是常數多項式, 不過由定義因為 0 多項式並找不到不為 0 的係數, 所以對 0 多項式我們不能說它的 degree 為 0. 通常我們就不訂 0 的 degree (有的書定義 deg(0) = - $ \infty$). 接下來我們來看 degree 的性質.

Lemma 7.2.2   若 f (x) 和 g(x) 都是 F[x] 中的非 0 多項式, 則

deg(f (x) . g(x)) = deg(f (x)) + deg(g(x)).

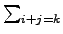証 明. 若 deg(f (x)) = n 且 deg(g(x)) = m 也就是說 f (x) = a0 + a1x + ... + anxn 及 g(x) = b0 + b1x + ... + bmxm, 其中 an$ \ne$ 0 且 bm$ \ne$ 0. 畢瓞 f (x) . g(x) = $ \sum$ckxk, 其中 ck = $ \sum_{i+j=k}^{}$ai . bj. 首先我們證明當 k > n + m 時 ck = 0. 若 i$ \le$n 且 j$ \le$m, 則 i + j$ \le$n + m. 由此知當 k > n + m 時若 i + j = k, 則 i > n 或 j > m. 也就是說 ai = 0 或 bj = 0. 故知當 k > n + m 時 ck = 0. 而當 k = n + m 時, 考� i + j = k 我們也可知唯有當 i = n 且 j = m 時 ai$ \ne$ 0 且 bj$ \ne$ 0. 換句話說 cn + m = an . bm. 由於 F 是一個 field, 所以 F 沒有 zero divisor, 故由 an$ \ne$ 0 且 bm$ \ne$ 0 可得 cn + m$ \ne$ 0. 換句話說 deg(f (x) . g(x)) = n + m. $ \qedsymbol$

由 Lemma 7.2.2, 我們馬上可以知道 F[x] 的 zero divisor 和 unit 有哪些.

Proposition 7.2.3   令 F 是一個 field.
  1. F[x] 中沒有 zero divisor, 換句話說 F[x] 是一個 integral domain.
  2. F[x] 中的 unit 就是所有非 0 的常數.

証 明. (1) 任取 f (x), g(x) $ \in$ F[x] 且皆不為 0. 若 deg(f (x)) = n 且 deg(g(x)) = m, 則由 Lemma 7.2.2 知 deg(f (x) . g(x)) = n + m. 換句話說, f (x) . g(x) 的 xn + m 項係數不為 0. 故知 f (x) . g(x) 不為 0 多項式. 故得證 F[x] 沒有 zero divisor.

(2) 若 f (x) 是 F[x] 中的一個 unit, 依定義知存在 g(x) $ \in$ F[x] 使得 f (x) . g(x) = 1. 因為 1 是常數多項式其 degree 為 0, 故由 Lemma 7.2.2 知 deg(f (x) . g(x)) = deg(f (x)) + deg(g(x)) = 0. 又 deg(f (x))$ \ge$ 0 且 deg(g(x))$ \ge$ 0, 故得 deg(f (x)) = 0 換句話說 f (x) 是常數多項式. 又 0 不可能是 unit, 故得 f (x) 是一個非 0 的常數. 反之, 若 f (x) = c 是一個非 0 的常數, 也就是 c $ \in$ F 且 c$ \ne$ 0. 因 F 是一個 field, 在 F 中可以找到 c 的 inverse c-1. 故令 g(x) = c-1 $ \in$ F[x], 則 f (x) . g(x) = 1. 故知 f (x) = c 是一個 unit. $ \qedsymbol$

接下來我們來看 polynomial ring 的餘式定理.

Theorem 7.2.4 (Euclid's Algorithm)   若 F 是一個 field, 給定兩 polynomials f (x), g(x) $ \in$ F[x], 其中 g(x)$ \ne$ 0, 則存在 h(x), r(x) $ \in$ F[x] 滿足 f (x) = h(x) . g(x) + r(x), 其中 r(x) = 0 或 deg(r(x)) < deg(g(x)).

証 明. 首先要注意, 這裡的餘式 r(x) 由於可能是 0, 而 0 又沒有 degree, 所以我們不能只說 deg(r(x)) < deg(g(x)), 而必須加上 r(x) = 0 這個可能性.

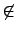我們利用和 Theorem 7.1.1 相似的證明考� W = {f (x) - l (x) . g(x) | l (x) $ \in$ F[x]} 這一個集合. 如果 0 $ \in$ W, 也就是說存在 h(x) $ \in$ F[x] 使得 f (x) - h(x) . g(x) = 0, 故得證 r(x) = 0. 如果 0 $ \not\in$W, 則令 r(x) $ \in$ W 是 W 中 degree 最小的 polynomial. 假設 deg(r(x)) = m 且 deg(g(x)) = n, 我們想用反證法證明 m < n. 如果 m$ \ge$n, 假設 r(x) 的最高次 xm 項的係數為 a, 而 g(x) 的最高次 xn 項係數為 b. 由於 b $ \in$ F 且 b$ \ne$ 0, 考� s(x) = r(x) - ((a . b-1)xm - n) . g(x) 這個多項式. 由於 r(x) 和 ((a . b-1)xm - n) . g(x) 的最高次 xm 的係數皆為 a, 故知 deg(s(x)) < m = deg(r(x)). 另� 由假設 r(x) $ \in$ W 知存在 l (x) $ \in$ F[x] 使得 r(x) = f (x) - l (x) . g(x). 故得

s(x) = f (x) - l (x) . g(x) - ((a . b-1)xm - n) . g(x) = f (x) - (l (x) + (a . b-1)xm - n) . g(x) $\displaystyle \in$ W.

也就是說 s(x) 是 W 中一個比 r(x) degree 小的 polynomial, 此和 r(x) 是 W 中 degree 最小的假設相矛盾. 故得 m < n 也就是說存在 h(x) $ \in$ F[x] 使得 r(x) = f (x) - h(x) . g(x) 且 deg(r(x)) < deg(g(x). 故得證本定理. $ \qedsymbol$

Remark 7.2.5   這裡要強調一下, 在 Theorem 7.2.4 的証明中我們用到了 F 是一個 field 的性質 (即 g(x) 的最高次係數 b 的 inverse b-1 存在). 所以 Theorem 7.2.4 並不能套用到係數為一般的 ring 的 polynomials 上. 事實上在 $ \mathbb {Z}$[x] 中就沒有餘式定理. 例如考� f (x) = x2, g(x) = 2x 我們就沒辦法找到整係數的多項式 h(x) 使得 f (x) - h(x) . g(x) = 0 或是 deg(f (x) - h(x) . g(x)) < deg(g(x)).

我們曾利用整數的餘數定理 (Theorem 7.1.1) 證得 $ \mathbb {Z}$ 中的 ideal 皆是 principle ideal (Theorem 7.1.2). 同樣的利用餘式定理 (Theorem 7.2.4), 我們可得以下的定理.

Theorem 7.2.6   若 F 是一個 field, 則 F[x] 中的 ideal 都是 principle ideal.

証 明. 任取 F[x] 的一個 ideal, I. 我們希望在 I 中找到一元素 g(x) 使得 $ \bigl($g(x)$ \bigr)$ = I. 令 g(x) 是 I 中 degree 最小的 polynomial, 我們希望證得 $ \bigl($g(x)$ \bigr)$ = I.

首先由於 g(x) $ \in$ I 所以當然 $ \bigl($g(x)$ \bigr)$ $ \subseteq$ I. 反之, 要證明 I $ \subseteq$ $ \bigl($g(x)$ \bigr)$ 也就是說任取 f (x) $ \in$ I 都要找到 h(x) $ \in$ F[x] 使得 f (x) = h(x) . g(x). 利用 Theorem 7.2.4 我們知道存在 h(x), r(x) $ \in$ F[x] 使得 f (x) = h(x) . g(x) + r(x) 其中 r(x) = 0 或 deg(r(x)) < deg(g(x)). 然而 g(x), f (x) $ \in$ I, 故得 r(x) = f (x) - h(x) . g(x) $ \in$ I. 如果 r(x)$ \ne$ 0, 表示 r(x) 是 I 中一個比 g(x) degree 還小的 polynomial, 這和當初 g(x) 的選取相矛盾. 故知 r(x) = 0, 即 f (x) = h(x) . g(x) $ \in$ $ \bigl($g(x)$ \bigr)$. $ \qedsymbol$

接下來要談 F[x] 上多項式的分解. 所以還是給因式, 公因式和最大公因式下一個定義.

Definition 7.2.7   令 f (x), g(x) $ \in$ F[x].
  1. 若 d (x) $ \in$ F[x] 且存在 h(x) $ \in$ F[x] 使得 f (x) = h(x) . d (x), 則稱 d (x) 是 f (x) 的一個 divisor, 記做 d (x) | f (x).
  2. 若 l (x) $ \in$ F[x], 且 l (x) | f (x) 及 l (x) | g(x), 則稱 l (x) 為 f (x), g(x) 的 common divisor.
  3. 若 d (x) $ \in$ F[x] 是 f (x), g(x) 的 common divisor 中 degree 最大的 polynomial, 則稱 d (x) 為 f (x), g(x) 的 greatest common divisor.

要注意這裡 greatest common divisor 並不唯一. 有的書會定 greatest common divisor 是所有 common divisor 中 degree 最大且最高次係數為 1 的 polynomial, 若在此定義之下 greatest common divisor 就唯一了.

一般可以利用所謂的輾轉相除法將兩個多項式的 greatest common divisor 求出來, 在這裡我們將利用 Theorem 7.2.6 找到 greatest common divisor 並得到其基本性質.

Proposition 7.2.8   給定 f (x), g(x) $ \in$ F[x], 則存在 d (x) $ \in$ F[x] 滿足 $ \bigl($d (x)$ \bigr)$ = $ \bigl($f (x)$ \bigr)$ + $ \bigl($g(x)$ \bigr)$ 且 d (x) 為 f (x), g(x) 的 greatest common divisor

証 明. 由 Theorem 7.1.2 知存在 d (x) $ \in$ F[x] 使得 $ \bigl($d (x)$ \bigr)$ = $ \bigl($f (x)$ \bigr)$ + $ \bigl($g(x)$ \bigr)$. 接著我們要證明這個 d (x) $ \in$ F[x] 是 f (x), g(x) 的 greatest common divisor. 首先當然是要證 d (x) 是 f (x), g(x) 的 common divisor. 然而因 f (x) $ \in$ $ \bigl($f (x)$ \bigr)$ $ \subseteq$ $ \bigl($f (x)$ \bigr)$ + $ \bigl($g(x)$ \bigr)$ = $ \bigl($d (x)$ \bigr)$, 故知存在 h(x) $ \in$ F[x] 使得 f (x) = h(x) . d (x). 也就是說 d (x) | f (x). 同理, 由 g(x) $ \in$ $ \bigl($d (x)$ \bigr)$ 可得 d (x) | g(x). 故知 d (x) 是 f (x), g(x) 的 common divisor.

那為甚麼 d (x) 會是 f (x), g(x) 的 common divisor 中 degree 最大的呢? 由於 d (x) $ \in$ $ \bigl($d (x)$ \bigr)$ = $ \bigl($f (x)$ \bigr)$ + $ \bigl($g(x)$ \bigr)$, 我們知道存在 m(x), n(x) $ \in$ F[x] 使得 d (x) = m(x) . f (x) + n(x) . g(x). 然而若 l (x) 是 f (x), g(x) 的 common divisor, 即 l (x) | f (x) 且 l (x) | g(x), 知存在 r(x), s(x) $ \in$ F[x] 使得 f (x) = r(x) . l (x) 且 g(x) = s(x) . l (x). 因此得

d (x) = m(x) . (r(x) . l (x)) + n(x) . (s(x) . l (x)) = (m(x) . r(x) + n(x) . s(x)) . l (x).

也就是說 l (x) | d (x). 所以知 d (x) 是所有 f (x), g(x) 的 common divisor 中 degree 最大的. $ \qedsymbol$

Proposition 7.2.8 不只告訴我們如何找到 greatest common divisor, 事實上在證明中我們也證得 greatest common divisor 的兩個重要性質.

Corollary 7.2.9   令 f (x), g(x) $ \in$ F[x] 且 d (x) 為 f (x), g(x) 的 greatest common divisor, 則 d (x) 符合以下兩性質:
  1. 存在 m(x), n(x) $ \in$ F[x] 滿足 d (x) = m(x) . f (x) + n(x) . g(x).
  2. 假設 l (x) | f (x) 且 l (x) | g(x), 則 l (x) | d (x).

一般在一個 ring 中元素的分解, 我們是不將 unit 列入考�. 例如在 $ \mathbb {Z}$ 中的分解我們都不將 1 和 -1 列為因數來考�. 在 F[x] 中的 units 是所有非 0 的常數多項式 (Proposition 7.2.3), 所以我們也不考憧早怓偺u正的 divisor. 因此我們有以下不可分解多項式 (irreducible element) 的定義.

Definition 7.2.10   考� F[x] 中的元素 p(x).
  1. 若對任意滿足 d (x) | p(x) 的 d (x) $ \in$ F[x], 皆有 d (x) = c 或 d (x) = c . p(x), 其中 0$ \ne$c $ \in$ F, 則稱 p(x) 是一個 irreducible element.
  2. 若對任意滿足 p(x) | f (x) . g(x) 的 f (x), g(x) $ \in$ F[x] 皆有 p(x) | f (x) 或 p(x) | g(x), 則稱 p(x) 是一個 prime element.

簡單來說一個 irreducible element 表示它不可以寫成兩個 degree 比它小的 polynomial 的乘積. 很顯然 irreducible 和 prime 這兩種定義是不一樣的, 不過下一個定理告訴我們在 F[x] 中這兩種定義的 polynomial 是相同的.

Proposition 7.2.11   在 F[x] 中若 p(x) 是一個 irreducible element, 則 p(x) 是一個 prime element. 反之, 若 p(x) 是一個 prime element, 則 p(x) 是一個 irreducible element.

証 明. 首先我們證若 p(x) 是 irreducible 則 p(x) 是 prime. 也就是說假設已知 p(x) 是 irreducible. 任取 p(x) | f (x) . g(x) 我們要證明: p(x) | f (x) 或 p(x) | g(x). 然而 p(x) | f (x) . g(x) 表示存在 r(x) $ \in$ F[x] 使得 f (x) . g(x) = r(x) . p(x). 如果 p(x) | f (x) 那麼就得到我們要證的, 所以我們只要討論 p(x)$ \nmid$f (x) 的情況. 此時我們考� p(x), f (x) 的 greatest common divisor 令之為 d (x). 由於 d (x) | p(x) 故由 p(x) 是 irreducible 的假設知 d (x) = c 或 d (x) = c . p(x), 其中 0$ \ne$c $ \in$ F. 然而 d (x) 不可能等於 c . p(x), 否則由 d (x) 是 p(x), f (x) 的 common divisor 知 p(x) = c-1 . d (x) | f (x) (注意 c 是 F[x] 的 unit). 此和 p(x)$ \nmid$f (x) 矛盾. 因此知 d (x) = c, 由 Corollary 7.2.9 知存在 n(x), m(x) $ \in$ F[x] 滿足 c = n(x) . p(x) + m(x) . f (x). 等式兩邊乘上 c-1 . g(x) 得
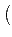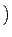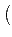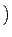g(x) = c-1$\displaystyle \bigl($n(x) . g(x)$\displaystyle \bigr)$ . p(x) + c-1$\displaystyle \bigl($m(x) . (f (x) . g(x))$\displaystyle \bigr)$  
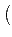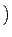  = c-1$\displaystyle \bigl($n(x) . g(x) + m(x) . r(x)$\displaystyle \bigr)$ . p(x),  

所以 p(x) | g(x).

反之, 若已知 p(x) 是一個 prime element 我們要證明 p(x) 是 irreducible. 也就是證明若 d (x) | p(x), 則 d (x) = c 或 d (x) = c . p(x). 然而 d (x) | p(x) 表示存在 r(x) $ \in$ F[x] 滿足 p(x) = r(x) . d (x), 也就是說 p(x) | r(x) . d (x). 故由 p(x) 是 prime 的假設, 我們得 p(x) | d (x) 或 p(x) | r(x). 當 p(x) | d (x) 時, 表示存在 s(x) $ \in$ F[x] 使得 d (x) = s(x) . p(x). 由原先假設 p(x) = r(x) . d (x) 知 d (x) = (s(x) . r(x)) . d (x). 也就是說 d (x) . (s(x) . r(x) - 1) = 0, 利用 F[x] 沒有 zero divisor (Proposition 7.2.3) 及 d (x)$ \ne$ 0, 知 s(x) . r(x) = 1, 即 s(x) 是 unit. 也就是說 s(x) 是一個常數多項式 c, 故得 d (x) = s(x) . p(x) = c . p(x). 當 p(x) | r(x) 時, 表示存在 s(x) $ \in$ F[x] 滿足 r(x) = s(x) . p(x). 故由 p(x) = d (x) . r(x) = d (x) . (s(x) . p(x)) 得 d (x) . s(x) = 1. 表示 d (x) 是 F[x] 的 unit, 即 d (x) = c. $ \qedsymbol$

從前面幾個定理看來, 不難發� $ \mathbb {Z}$ 的很多重要性質都可以推導到 F[x] 上. 大家應該也會猜測 F[x] 也會有和 $ \mathbb {Z}$ 相似的唯一分解定理. 前面提過在談分解時我們不會把 unit 的差異納入考�, 這就是為甚麼我們在 $ \mathbb {Z}$ 中談因數時只考憧蕉�. 在 F[x] 中若 d (x) 是 f (x) 的 divisor, 即存在 h(x) $ \in$ F[x] 使得 f (x) = d (x) . h(x), 則對任意 F[x] 中不等於 0 的 常數 c 因為其為 F[x] 的 unit, 當然我們知 c-1 . h(x) $ \in$ F[x]. 因此由 f (x) = (c . d (x)) . (c-1 . h(x)) 得到 c . d (x) 也是 f (x) 的 divisor. 所以對所有的 0$ \ne$c $ \in$ F, 從分解的觀點我們將 d (x) 和 c . d (x) 看成是 f (x) 一樣的 divisor. 我們需要一個方法來選取一個適當的 c . d (x) 來當 f (x) 的 divisor. 一般習慣上我們習慣選取 c 使得 c . d (x) 的最高次項係數為 1, 因此有以下的定義.

Definition 7.2.12   若 f (x) $ \in$ F[x] 且 f (x) 的最高次項係數為 1 則稱 f (x) 為一個 monic polynomial.

以下一個 Lemma 告訴我們選取 monic polynomial 的好處.

Lemma 7.2.13   假設 p(x), q(x) $ \in$ F[x] 都是 monic irreducible element 且 p(x) | q(x), 則 p(x) = q(x).

証 明. 由於 q(x) 是 irreducible, q(x) 的 divisor 只能是常數 c 或 c . q(x) 這種形式. 故由 p(x) 不是常數 (因假設是 irreducible) 且 p(x) | q(x) 知存在 c $ \in$ F 滿足 p(x) = c . q(x). 不過由於 p(x), q(x) 都是 monic polynomial, 它們的最高次項係數都是 1. 故得 c = 1, 即 p(x) = q(x). $ \qedsymbol$

畢b我們就來看 F[x] 上的唯一分解性質應該是甚麼樣子.

Theorem 7.2.14   假設 f (x) $ \in$ F[x] 且 deg(f (x))$ \ge$1, 則存在 c $ \in$ F 以及 p1(x),..., pr(x), 其中這些 pi(x) 是相異的 monic irreducible elements, 滿足

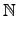
f (x) = c . p1(x)n1 ... pr(x)nr,    ni 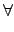$\displaystyle \in$ $\displaystyle \mathbb {N}$,$\displaystyle \forall$i $\displaystyle \in$ {1,..., r}.

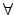如果 f (x) 可以分解成另� 的形式 f (x) = d . q1(x)m1 ... qs(x)ms, 其中 d $ \in$ F 而且這些 qi(x) 是相異的 monic irreducible elements, 則 c = d, r = s 且經過變換順序可得 pi(x) = qi(x), ni = mi, $ \forall$ i $ \in$ {1,..., r}.

証 明. 我們利用和 Theorem 7.1.8 類似的方法來證明. Theorem 7.1.8 用到了數學歸納法, 這裡雖然我們談的不是整數, 不過由於我們有 degree 這個很好的工具將 F[x] 的元素送到整數, 所以我們可以對 degree 做 induction.

首先來看存在性 (也就是 f (x) 可以寫成所要求的形式): 當 deg(f (x)) = 1 時由於 f (x) = ax + b, 其中 0$ \ne$a $ \in$ F, 所以我們可以將 f (x) 寫成 a . (x + b . a-1). 很顯然的 x + b . a-1 不可能寫成兩個 degree 小於 1 的 polynomial 的乘積, 所以 x + b . a-1 是一個 monic irreducible element. 所以在這情況存在性是成立的. 接著假設對所有 degree 介於 1 和 n - 1 間的 polynomials 存在性是成立的. 畢b考� deg(f (x)) = n 情況. 如果 f (x) 是 irreducible 且其最高次項係數為 a, 那麼 a-1 . f (x) 當然是一個 monic irreducible element, 所以 f (x) = a . (a-1 . f (x)), 存在性自然成立. 如果 f (x) 不是 irreducible, 則知 f (x) = g(x) . h(x) 其中 g(x), h(x) $ \in$ F[x] 且 1$ \le$deg(g(x)) < n 及 1$ \le$deg(h(x)) < n. 故利用歸納假設知

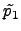
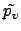
g(x) = c1 . p1(x)n1 ... pu(x)nu 和 h(x) = c2 . $\displaystyle \tilde{p_1}$(x)m1 ... $\displaystyle \tilde{p_v}$(x)mv,

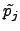
其中 pi(x), $ \tilde{p_j}$(x) 都是 monic irreducible elements, 所以將相同的 monic irreducible elements 合併, 得證 f (x) 也可以寫成所要求的形式.

接下來看唯一性: 假設 deg(f (x)) = 1, 由於 f (x) = ax + b, 其唯一性自然成立. 接著假設唯一性對所有 degree 介於 1 和 n - 1 間的 polynomials 都成立, 畢b考� deg(f (x)) = n 的情況. 假設

f (x) = c . p1(x)n1 ... pr(x)nr = d . q1(x)m1 ... qs(x)ms,

其中 c, d $ \in$ F, pi(x) 是兩兩相異, qj(x) 也是兩兩相異, 而且 pi(x), qj(x) 都是 monic irreducible element. 首先觀察, 由於 pi(x), qj(x) 都是 monic, 所以 c 和 d 應該都是 f (x) 最高次項的係數. 一個 polynomial 的最高次項應該是唯一的, 故得 c = d. 接著由於 p1(x) 是 irreducible 所以由 Proposition 7.2.11 知其為 prime, 故由 p1(x) | f (x) = cq1(x)m1 ... qs(x)ms 知存在某個 j $ \in$ {1,..., s} 滿足 p1(x) | qj(x). 變換一下順序我們可以假設 p1(x) | q1(x), 故利用 p1(x) 和 q1(x) 都是 monic irreducible element 以及 Lemma 7.2.13 知 p1(x) = q1(x). 因此我們可將 f (x) 的分解改寫成

f (x) = c . p1(x)n1 . p2(x)n2 ... pr(x)nr = c . p1(x)m1 . q2(x)m2 ... qs(x)ms.

將上式移項再提出 c . p1(x), 我們可得

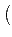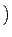
c . p1(x) . $\displaystyle \bigl($p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr - p1(x)m1 - 1 . q2(x)m2 ... qs(x)ms$\displaystyle \bigr)$ = 0.

由於 c . p1(x)$ \ne$ 0 且 F[x] 是 integral domain, 我們得

p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr - p1(x)m1 - 1 . q2(x)m2 ... qs(x)ms = 0.

畦O g(x) = p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr. 由於

deg(g(x)) = deg(f (x)) - deg(p1(x)) < deg(f (x)) = n

且

g(x) = p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr = p1(x)m1 - 1 . q2(x)m2 ... qs(x)ms

是 g(x) 的兩個分解, 故利用歸納法假設我們有 r = s 且 p1(x) = q1(x),..., pr(x) = qr(x) 以及 n1 = m1, n2 = m2,..., nr = mr, 故得證唯一性. $ \qedsymbol$

next up previous
下一頁: Polynomials over the Integers 上一頁: 一些常見的 Rings 前一頁: The Ring of Integers
Administrator 2005-06-18