


�U�@��: Quotient Field of an
�W�@��: �@�DZ`���� Rings
�e�@��: Ring of Polynomials over
�e�@���`�����G���M���i�H�M�Ψ즳�z�Y�ƪ� polynomials,
���o���৹����㪺�M�Ψ��Y�ƪ� polynomials.
�o�@���ڭ̱N�ݬݾ�Y�ƩM���z�Y�� polynomials �����P.
�̫�A�Q�Ϋe�����`�����ƪ��ߤ@���ѩʥH�Φ��z�Y�ƪ� polynomial ring
���ߤ@���ѩ�, �o���Y�ƪ� polynomial ring ���ߤ@���ѩ�.
�ڭ̥O
 [x] ���ܩҦ����z�Y�� polynomials �Ҧ������X�B�O
[x] ���ܩҦ����z�Y�� polynomials �Ҧ������X�B�O
 [x]
���ܩҦ���Y�� polynomials �Ҧ������X. �e���w��
[x]
���ܩҦ���Y�� polynomials �Ҧ������X. �e���w��
 [x]
�Τ@�몺�[�k�M���k�i�Φ��@�� ring, �ڭ̺٤��� polynomial ring over
[x]
�Τ@�몺�[�k�M���k�i�Φ��@�� ring, �ڭ̺٤��� polynomial ring over
 . �P�z�ڭ̤]�i�H�ҥX
. �P�z�ڭ̤]�i�H�ҥX
 [x] �]�O�@�� ring, �ڭ̺٤���
polynomial ring over
[x] �]�O�@�� ring, �ڭ̺٤���
polynomial ring over
 .
.
 [x] �� 0 �M 1 �M
[x] �� 0 �M 1 �M
 [x] �� 0 �M 1 �ۦP. �ڭ̤]�i�b
[x] �� 0 �M 1 �ۦP. �ڭ̤]�i�b
 [x] ���w�q degree (�ϥ��i�H��
[x] ���w�q degree (�ϥ��i�H��
 [x] �ݦ�
[x] �ݦ�
 [x] ���l���X).
�ҥH�Q�ΩM Lemma 7.2.3 �ۦP���ҩ�, �ڭ̥i�o
[x] ���l���X).
�ҥH�Q�ΩM Lemma 7.2.3 �ۦP���ҩ�, �ڭ̥i�o
 [x] �O�@��
integral domain.
[x] �O�@��
integral domain.
 [x] �M
[x] �M
 [x] �̤j�����P�O
[x] �̤j�����P�O
 [x] ���Ҧ��D
0 ���`�Ƴ��O unit, �M��
[x] ���Ҧ��D
0 ���`�Ƴ��O unit, �M��
 [x] ���u�� ±1 �o��ӱ`�Ƭ���
unit. �o�O�]���Q�� Lemma 7.2.3 ���ҩ��ڭ̪��D
[x] ���u�� ±1 �o��ӱ`�Ƭ���
unit. �o�O�]���Q�� Lemma 7.2.3 ���ҩ��ڭ̪��D
 [x] ����
unit �� degree �@�w�O 0, �ҥH�u���`�Ƥ �i��O
[x] ����
unit �� degree �@�w�O 0, �ҥH�u���`�Ƥ �i��O
 [x] �� unit,
�M�Ӧ]�ڭ̥u�Ҽ��Y��, �ҥH�b
[x] �� unit,
�M�Ӧ]�ڭ̥u�Ҽ��Y��, �ҥH�b
 ���� unit � �i�H�O
���� unit � �i�H�O
 [x] ��
unit, �]�N�O ±1. �]���o�̧ڭ̥��������j�a, �b
[x] ��
unit, �]�N�O ±1. �]���o�̧ڭ̥��������j�a, �b
 [x]
���ͤ��Ѯɭn�N�`�ƪ����ѦC�J�Ҽ.
[x]
���ͤ��Ѯɭn�N�`�ƪ����ѦC�J�Ҽ.
�b Remark 7.2.5 ���ڭ̴���
 [x] ���èS���l���w�z,
�ҥH�b
[x] ���èS���l���w�z,
�ҥH�b
 [x] ���i�Q�ξl���w�z�o�쪺�Ҧ� ideal ���O principle
ideal (Theorem 7.2.6) ��
[x] ���i�Q�ξl���w�z�o�쪺�Ҧ� ideal ���O principle
ideal (Theorem 7.2.6) ��
 [x] �N���@�w��.
�ƹ�W�ڭ̥i�H�b
[x] �N���@�w��.
�ƹ�W�ڭ̥i�H�b
 [x] �����@�� (���M���u�@��) ideal �����O
principle ideal.
[x] �����@�� (���M���u�@��) ideal �����O
principle ideal.
Example 7.3.1
�ڭ̭n�����b

[
x] ��
I = (2) + (
x) ���O principle ideal. ���]
I
�O principle ideal, �Y�s�b
f (
x)


[
x] �ϱo
I =
 f
f (
x)

.
�Q�� 2
 I
I, �ڭ̱o��
2

 f
f (
x)

, �]�N�O�s�b
h(
x)


[
x]
����
2 =
h(
x)
. f (
x). �Q�� degree ���W�i��
deg(
f (
x)) = 0,
�]�N�O��
f (
x) �O�@�ӱ`��
c 

. ��b�Q��
x  I
I =
 c
c
���s�b
g(
x)


[
x] �ϱo
x =
c . g(
x). �`�N
c . g(
x)
�o�@�Ӧh���������Y�Ƥ@�w�O
c ������ (�O�ѤF
g(
x)


[
x], �ҥH
g(
x) ���Y�Ƴ��O���). �]����
x =
c . g(
x) ��
x
�o�@�Ӧh�������Y�����ӬO
c ������. �M��
x �o�@�Ӧh�����u��
x
�o�@���B��Y�ƬO 1, �G�o
c | 1, �]�N�O
c = ±1. �]
c �O
unit, Lemma
6.2.4 �i�D�ڭ�
I =
 c
c
=

[
x], ���y�ܻ�
1
 I
I =

2

+
 x
x
. �Q��

2

+
 x
x
���w�q���o���ܦs�b
n(
x),
m(
x)


[
x] �ϱo
1 = 2
. n(
x) +
x . m(
x). ���L
x . m(
x) �S���`�ƶ�, ��
2
. n(
x) ���`�ƶ��@�w�O 2 ������, �ҥH
2
. n(
x) +
x . m(
x) ���`�ƶ��@�w���i�ର 1. �G��
n(
x),
m(
x)


[
x] ��
1 = 2
. n(
x) +
x . m(
x) ���i�ন��.
���٬o�ͩ�ڭ̪����]
I �O principle ideal, �G�o
I =

2

+
 x
x
���i��O

[
x] �� principle ideal.
�n�F�J�M
 [x] ���� ideal ���@�w�O principle ideal
����ڭ̴N����� Proposition 7.2.11 ����k�o��
[x] ���� ideal ���@�w�O principle ideal
����ڭ̴N����� Proposition 7.2.11 ����k�o��
 [x] ����
irreducible element �N�O prime element �F.
����γo�M��k�ä����ܵ��G�|��,
�]�����i��Υt�@�M��k�i�H�o��Q�n�����G��!
�S���ڭ̱N�|�ҩ��b
[x] ����
irreducible element �N�O prime element �F.
����γo�M��k�ä����ܵ��G�|��,
�]�����i��Υt�@�M��k�i�H�o��Q�n�����G��!
�S���ڭ̱N�|�ҩ��b
 [x] ���� irreducible element �M prime
element �O�ۦP��, ���L�ڭ̭n�o�i�t�@�M����k�ӱo��.
[x] ���� irreducible element �M prime
element �O�ۦP��, ���L�ڭ̭n�o�i�t�@�M����k�ӱo��.
�o�Ӥ�k���N�O�n�J�A�e������
 [x] �M
[x] �M
 [x] �̤j�����P�N�O�b
[x] �̤j�����P�N�O�b
 [x] ���n�Ҽ�`�ƪ�����. ���w
f (x) = a0 + a1x + ... + anxn
[x] ���n�Ҽ�`�ƪ�����. ���w
f (x) = a0 + a1x + ... + anxn 
 [x] �n�N f (x) ���Ѧ� degree ����p�� polynomials
�ۭ����e, �i�H���Ҽ�i���i�H���X�@�ӱ`�ƥX�� (�]���Y�o�ӱ`�Ƥ��O
±1 ����b
[x] �n�N f (x) ���Ѧ� degree ����p�� polynomials
�ۭ����e, �i�H���Ҽ�i���i�H���X�@�ӱ`�ƥX�� (�]���Y�o�ӱ`�Ƥ��O
±1 ����b
 [x] ���o�N��O�@��``����''������).
�i�H���X�ƻ�`�ƥX�өO? �j�a���|�Q�촣�X���ǫY��
a0, a1,..., an
���̤j���]�Ƨa! �ҥH�ڭ̦��H�U²������n�����G.
[x] ���o�N��O�@��``����''������).
�i�H���X�ƻ�`�ƥX�өO? �j�a���|�Q�촣�X���ǫY��
a0, a1,..., an
���̤j���]�Ƨa! �ҥH�ڭ̦��H�U²������n�����G.
Lemma 7.3.2
�Y
f (
x)


[
x] �O�@�ӫD 0 �� polynomial, �h
f (
x) �i�ߤ@�g��
f (
x) =
c . f*(
x), �䤤
c 

,
f*(
x)


[
x] �B
f*(
x)
���Y�ƪ��̤j���]�ƬO 1.
�� ��.
�����ҩ��s�b��: �Y
f (
x) =
a0 +
a1x +
... +
anxn, �O
d = gcd(
a0,
a1,...,
an). �ѳ̤j���]�ƪ��ʽ誾
a0 =
d . b0,
a1 =
d . b1,...,
an =
d . bn �B
gcd(
b0,
b1,...,
bn) = 1. �G�i�N
f (
x) �g��
d . (
b0 +
b1x +
... +
bnxn) ���ҭn�D���Φ�.
�����ҩ��ߤ@��: ���]
f (x) = c . f*(x), �䤤
c 
 �B
f*(x)
�B
f*(x) 
 [x]. �N c ���J f*(x) ���U���Y�Ƥ�, �� f (x)
���Ҧ��Y��
a0, a1,..., an ���|�O c ������. �]�N�O c �O
a0, a1,..., an �����]��. �p�G
c
[x]. �N c ���J f*(x) ���U���Y�Ƥ�, �� f (x)
���Ҧ��Y��
a0, a1,..., an ���|�O c ������. �]�N�O c �O
a0, a1,..., an �����]��. �p�G
c d = gcd(a0, a1,..., an),
�h f*(x) ���Y�Ƥ��|�� d /c �o�@�Ӥ��O 1 �����]��, ���M
f*(x) ���U���Y�ƪ��̤j���]�Ƭ� 1 �ۥ٬�. �G�o d = c, �]�N�O��
d . f*(x) = d . (b0 + b1x + ... + bnxn). �̫�]
d = gcd(a0, a1,..., an),
�h f*(x) ���Y�Ƥ��|�� d /c �o�@�Ӥ��O 1 �����]��, ���M
f*(x) ���U���Y�ƪ��̤j���]�Ƭ� 1 �ۥ٬�. �G�o d = c, �]�N�O��
d . f*(x) = d . (b0 + b1x + ... + bnxn). �̫�]
 [x] �O
integral domain, �ڭ̱o
f*(x) = b0 + b1x + ... + bnxn.
[x] �O
integral domain, �ڭ̱o
f*(x) = b0 + b1x + ... + bnxn.

���F Lemma 7.3.2, �ڭ̦��H�U���w�q.
Definition 7.3.3
�Y
f (
x)


[
x] �i�g��
f (
x) =
c . f*(
x), �䤤
c 

,
f*(
x)


[
x] �B
f*(
x) ���Y�ƪ��̤j���]�ƬO 1. �h��
c ��
f (
x) ��
content, �O��
c(
f ). �Y
f (
x)


[
x] �B
c(
f )= 1, �h��
f (
x) �O�@��
primitive polynomial.
��� c(f ) �N�O f (x) ���Ҧ��Y�ƪ��̤j���]��. Lemma 7.3.2
�i�D�ڭ̻����N��
f (x) 
 [x] ���i�H�g���� content ���W�@��
primitive polynomial. �ڭ̥i�H�N Lemma 7.3.2 ���s��
[x] ���i�H�g���� content ���W�@��
primitive polynomial. �ڭ̥i�H�N Lemma 7.3.2 ���s��
 [x]
��.
[x]
��.
Proposition 7.3.4
�Y
f (
x)


[
x] �O�@�ӫD 0 �� polynomial, �h
f (
x) �i�ߤ@�g��
f (
x) =
c . f*(
x), �䤤
c 

,
c > 0 �B
f*(
x)


[
x]
�O�@�� primitive polynomial.
�� ��.
�����ҩ��s�b��: �Y
f (
x) =
a0 +
a1x +
... +
anxn, �䤤
ai 

.
�ڭ̥i���@�����
m �ϱo
m . f (
x)


[
x] (��軡�O
m ��
�o��
ai ���������n). �J�M
m . f (
x)


[
x] �� Lemma
7.3.2 ���s�b�ʪ��s�b�����
a �H��
f*(
x)


[
x] �䤤
f*(
x) �O primitive polynomial, �ϱo
m . f (
x) =
a . f*(
x).
�G�o
f (
x) =
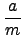 . f*
. f*(
x)
���ҭn�D���Φ�.
�ܩ�ߤ@�ʧڭ̰��]
f (x) = d . f*(x) = d' . g(x) �䤤 d, d'
���O�������z�Ʀ�
f*(x), g(x) 
 [x] ���O primitive polynomials.
�N d �M d' ���O�g�� a/b �M a'/b', �䤤
a, a', b, b'
[x] ���O primitive polynomials.
�N d �M d' ���O�g�� a/b �M a'/b', �䤤
a, a', b, b' 
 .
�ڭ̥i�o
.
�ڭ̥i�o
(a . b') . f*(x) = (a' . b) . g(x).
�O�ѤF
(
a . b')
. f*(
x),(
a' . b)
. g(
x)


[
x] �S�]
a . b',
a' . b 

�B
f*(
x),
g(
x) ���O primitive
polynomial, �� Lemma
7.3.2 ���ߤ@�ʪ�:
a . b' =
b . a'
(�Y
d =
d') �B
f*(
x) =
g(
x). �G�o�Ұߤ@��.

�� Proposition 7.3.4, �ڭ̥i�H�� content ���w�q���s��
 [x],
�H��ڭ̱N�|����N��
f (x)
[x],
�H��ڭ̱N�|����N��
f (x) 
 [x] �g��
f (x) = c(f ) . f*(x),
�䤤
0 < c(f )
[x] �g��
f (x) = c(f ) . f*(x),
�䤤
0 < c(f ) 
 �O f (x) �� content,
f*(x)
�O f (x) �� content,
f*(x) 
 [x] �O�@��
primitive polynomial.
[x] �O�@��
primitive polynomial.
��
f (x), g(x) 
 [x], �n�p��
f (x) . g(x) �� content,
���O�ܽ�����. �ڭ̥������� polynomial ���, ������z,
�A�q����̤j���]��. �ڭ̷��M�Ʊ�
f (x) . g(x) �� content �i�H��
f (x) �M g(x) �� contents �����D�X�N�n�F.
���ڭ̥��ݤ@�ӯS���Ҥl�N�O f (x) �M g(x) �� contents ���O 1
�����p.
[x], �n�p��
f (x) . g(x) �� content,
���O�ܽ�����. �ڭ̥������� polynomial ���, ������z,
�A�q����̤j���]��. �ڭ̷��M�Ʊ�
f (x) . g(x) �� content �i�H��
f (x) �M g(x) �� contents �����D�X�N�n�F.
���ڭ̥��ݤ@�ӯS���Ҥl�N�O f (x) �M g(x) �� contents ���O 1
�����p.
Lemma 7.3.5 (Gauss Lemma)
�Y
f (
x),
g(
x)


[
x] ���O primitive polynomials, �h
f (
x)
. g(
x) �]�O�@�� primitive polynomial.
�� ��.
�]
f (
x) =
anxn +
... +
a1x +
a0,
g(
x) =
bmxm +
... +
b1x +
b0,
�ڭ̭n�Τ��Ҫk�ҩ��Y
c(
f )=
c(
g) = 1, �h
c(
f . g) = 1. ���]
c(
f . g) =
d
1, ���@���
p �ϱo
p |
d, �]�N�O
p �㰣
f (
x)
. g(
x) ���Ҧ��Y��. �M�]
c(
f )=
c(
g) = 1, �G���s�b
ai,
bj �ϱo
p ai
ai �B
p bj
bj. �O
r �O�̤p����ƨϱo
p ar
ar (�]�N�O
p ar
ar, ������N��
i <
r,
p |
ai),
�P�˪��O
s �O�̤p����ƨϱo
p bs
bs. ��[��
f (
x)
. g(
x)
��
xr + s ���Y��:
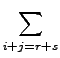 ai . bj
ai . bj.
���F
ar . bs �H� , ��L����
ai . bj �n���O
i <
r �N�O
j <
s. �_�h�Y
i >
r �B
j >
s ����
i +
j >
r +
s �N���i��ŦX
i +
j =
r +
s �F. �p�G
i <
r
�ѷ���
r �������
p |
ai, �G�������p�U
p |
ai . bj.
�P�z, �Y
j <
s �]�i�o
p |
ai . bj. �`�Ө���,
f (
x)
. g(
x) ��
xr + s �����Y�ư��F
ar . bs � ��L��
ai . bj ���i�Q
p �㰣. �M�ӷ��찲�]
p ar
ar �B
p bs
bs,
�G��
p ar . bs
ar . bs. �]�N�O��
f (
x)
. g(
x) ��
xr + s
�����Y�Ƥ��i�Q
p �㰣. �o�M���찲�]
p �i�㰣
f (
x)
. g(
x)
���C�@�����Y�Ƭۥ٬�. �G�����i��
c(
f . g)

1, �ҥH
f (
x)
. g(
x) �]�O primitive polynomial.

���F Gauss Lemma ���@�몺
f (x), g(x) 
 [x],
�ڭ̫ܧ֪��N�i�H�p��X
c(f . g).
[x],
�ڭ̫ܧ֪��N�i�H�p��X
c(f . g).
Proposition 7.3.6
�Y
f (
x),
g(
x)


[
x] ���O�D 0 �� polynomial, �h
c(f . g) = c(f ) . c(g).
�� ��.
�� Lemma
7.3.4 ���i�N
f (
x) �M
g(
x) ���O�g��
f (
x) =
c(
f )
. f*(
x) �M
g(
x) =
c(
g)
. g*(
x), �䤤
f*(
x) �M
g*(
x) ���O
primitive polynomials. �G�o
f (
x)
. g(
x) =
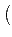 c
c(
f )
. c(
g)
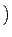 .
. 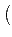 f*
f*(
x)
. g*(
x)
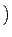
.
�A�� Lemma
7.3.4 ��
f (
x)
. g(
x) �i�ߤ@�g��
c(
f . g)
. h(
x)
�䤤
h(
x) �O primitive polynomial. �M�� Lemma
7.3.5 �i�D�ڭ�
f*(
x)
. g*(
x) �O primitive polynomial, �G�Ѱߤ@�ʪ�
f*(
x)
. g*(
x) =
h(
x) �B
c(
f )
. c(
g) =
c(
f . g).

���U�ӧڭ̭n��
 [x] �W������, �����n�Ϥ��@�U�b
[x] �W������, �����n�Ϥ��@�U�b
 [x] �M
[x] �M
 [x] �����㰣����. ���w
f (x), g(x)
[x] �����㰣����. ���w
f (x), g(x) 
 [x], �ڭ̻�
f (x) | g(x) in
[x], �ڭ̻�
f (x) | g(x) in
 [x] ���ܦs�b
h(x)
[x] ���ܦs�b
h(x) 
 [x] ����
g(x) = h(x) . f (x). �ӧڭ̻�
f (x) | g(x) in
[x] ����
g(x) = h(x) . f (x). �ӧڭ̻�
f (x) | g(x) in
 [x] ���ܦs�b
l (x)
[x] ���ܦs�b
l (x) 
 [x]
����
g(x) = l (x) . f (x). �o�̳̤j�����P�b�� h(x) �n�D���b
[x]
����
g(x) = l (x) . f (x). �o�̳̤j�����P�b�� h(x) �n�D���b
 [x], �� l (x) �n�b
[x], �� l (x) �n�b
 [x] �Y�i. �ҥH���i��o��
f (x) | g(x) in
[x] �Y�i. �ҥH���i��o��
f (x) | g(x) in
 [x] ��
f (x)
[x] ��
f (x) g(x) in
g(x) in
 [x] �����p.
[x] �����p.
Lemma 7.3.7
���]
f (
x),
g(
x)


[
x], �B
f (
x) �O�@�� primitive polynomial, �h
f (
x) |
g(
x) in

[
x] �Y�B�߭Y
f (
x) |
g(
x) in

[
x].
�� ��.
���]
f (
x) |
g(
x) in

[
x] ���ܦs�b
h(
x)


[
x] ����
g(
x) =
h(
x)
. f (
x). �M��
h(
x)


[
x] ���M�o
h(
x)


[
x],
�G��
f (
x) |
g(
x) in

[
x]. (�`�N�o�����ڭ̤��ݭn
f (
x) �O
primitive �����].)
�Ϥ�, �Y
f (x) | g(x) in
 [x], ���ܦs�b
l (x)
[x], ���ܦs�b
l (x) 
 [x] ����
g(x) = l (x) . f (x). �ڭ̧Ʊ���ұo
l (x)
[x] ����
g(x) = l (x) . f (x). �ڭ̧Ʊ���ұo
l (x) 
 [x]. �Q�� Lemma
7.3.4 �N l (x) �g��
l (x) = c(l ) . l*(x), �䤤 l*(x) �O
primitive polynomials. �G�o
g(x) = c(l ) . (l*(x) . f (x)). �]��
f (x) �M l*(x) ���O primitive polynomials, �G�Q�� Lemma
7.3.5 ��
l*(x) . f (x) �O primitive polynomial. �A�Q��
Lemma 7.3.4 ���ߤ@�ʪ� c(g) = c(l ). �]
c(g)
[x]. �Q�� Lemma
7.3.4 �N l (x) �g��
l (x) = c(l ) . l*(x), �䤤 l*(x) �O
primitive polynomials. �G�o
g(x) = c(l ) . (l*(x) . f (x)). �]��
f (x) �M l*(x) ���O primitive polynomials, �G�Q�� Lemma
7.3.5 ��
l*(x) . f (x) �O primitive polynomial. �A�Q��
Lemma 7.3.4 ���ߤ@�ʪ� c(g) = c(l ). �]
c(g) 
 , �G�o
c(l )
, �G�o
c(l ) 
 , �B�S
l*(x)
, �B�S
l*(x) 
 [x], �G��
l (x) = c(l ) . l*(x)
�o
l (x)
[x], �G��
l (x) = c(l ) . l*(x)
�o
l (x) 
 [x].
[x].

�P�˪�, �ڭ̤]�n�Ϥ��@�U�b
 [x] �M
[x] �M
 [x] �����Ѫ����P. �Y
f (x)
[x] �����Ѫ����P. �Y
f (x) 
 [x] �ڭ̻� f (x) �b
[x] �ڭ̻� f (x) �b
 [x] �i���Ѫ��� f (x) �i�g��
f (x) = g(x) . h(x), �䤤
g(x), h(x)
[x] �i���Ѫ��� f (x) �i�g��
f (x) = g(x) . h(x), �䤤
g(x), h(x) 
 [x] �B
deg(g(x)) �M
deg(h(x)) �Ҥp��
deg(f (x)). ���o����� f (x) �i�H�b
[x] �B
deg(g(x)) �M
deg(h(x)) �Ҥp��
deg(f (x)). ���o����� f (x) �i�H�b
 [x] �����Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x)
[x] �����Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x) 
 [x].
���L�U�@�� Lemma �i�D�ڭ̳o�O��o�쪺.
[x].
���L�U�@�� Lemma �i�D�ڭ̳o�O��o�쪺.
Lemma 7.3.8
���]
f (
x)


[
x] �B
f (
x) =
g(
x)
. h(
x) �䤤
g(
x),
h(
x)


[
x], �h�s�b
m(
x),
n(
x)


[
x] ����
f (
x) =
m(
x)
. n(
x) �B
deg(
m(
x)) = deg(
g(
x)) ��
deg(
n(
x)) = deg(
h(
x)).
�� ��.
�Q�� Lemma
7.3.4 ��
g(
x) =
c(
g)
. g*(
x) �B
h(
x) =
c(
h)
. h*(
x) �䤤
g*(
x),
h*(
x)


[
x] �B���O primitive polynomial.
�Q�� Proposition
7.3.6 ��
c(g) . c(h) = c(g . h) = c(f ),
�M��
f (
x)


[
x], �G
c(
g)
. c(
h) =
c(
f )


. �]���Y�O
m(
x) =
 c
c(
g)
. c(
h)
 . g*
. g*(
x)


[
x] ��
n(
x) =
h*(
x)


[
x], �h
| f (x) |
= |
g(x) . h(x) = 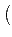 c(g) . g*(x) c(g) . g*(x)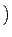 . . 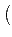 c(h) . h*(x) c(h) . h*(x)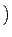 |
|
| |
= |
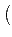 c(g) . c(h) c(g) . c(h)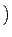 . g*(x) . h*(x) . g*(x) . h*(x) |
|
| |
= |
m(x) . n(x). |
|
�S
deg(m(x)) = deg(g*(x)) = deg(g(x)) �B deg(n(x)) = deg(h*(x)) = deg(h(x)).

�Ϥ��Y f (x) �b
 [x] �i�H���Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x)
[x] �i�H���Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x) 
 [x], �B m(x), n(x) ���O
[x], �B m(x), n(x) ���O
 [x] ���� unit. ����
�j�a�@�w����ѩ� m(x), n(x) �]�b
[x] ���� unit. ����
�j�a�@�w����ѩ� m(x), n(x) �]�b
 [x] ���ҥH f (x) �b
[x] ���ҥH f (x) �b
 [x]
���i�H����. ��ꤣ�M, �]�� m(x), n(x) �b
[x]
���i�H����. ��ꤣ�M, �]�� m(x), n(x) �b
 [x] �����O unit,
���i��b
[x] �����O unit,
���i��b
 [x] ���N�O unit �F. �Ҧp 2x + 2 �b
[x] ���N�O unit �F. �Ҧp 2x + 2 �b
 [x] �O
irreducible ���b
[x] �O
irreducible ���b
 [x] ��
2x + 2 = 2 . (x + 1), �ӥB 2 �M x + 1
�b
[x] ��
2x + 2 = 2 . (x + 1), �ӥB 2 �M x + 1
�b
 [x] �������O unit (�� 2 �b
[x] �������O unit (�� 2 �b
 [x] �O unit), �ҥH 2x + 2
�b
[x] �O unit), �ҥH 2x + 2
�b
 [x] �ä��O irreducible. �q�o�̬ݥX
[x] �ä��O irreducible. �q�o�̬ݥX
 [x] ���� irreducible
element �M
[x] ���� irreducible
element �M
 [x] �� irreducible element ���P.
[x] �� irreducible element ���P.
�^�U�@�U�ڭ̩w�q�ҿת� irreducible element �O�@�Ӥ������� divisor
�u�� unit �M �������W unit �o��اΦ�. �ѩ�
 [x] ���� unit �u��
1 �M -1 �ҥH�ڭ̦��H�U���w�q.
[x] ���� unit �u��
1 �M -1 �ҥH�ڭ̦��H�U���w�q.
Definition 7.3.9
�O
p(
x)


[
x]
- �Y p(x) �b
 [x] ���� divisor �u�� ±1 �M ±p(x),
�h�� p(x) �O
[x] ���� divisor �u�� ±1 �M ±p(x),
�h�� p(x) �O
 [x] �� irreducible element.
[x] �� irreducible element.
- �Y��Ҧ�����
p(x) | f (x) . g(x) ��
f (x), g(x)

 [x]
����
p(x) | f (x) ��
p(x) | g(x) �h�� p(x) �O
[x]
����
p(x) | f (x) ��
p(x) | g(x) �h�� p(x) �O
 [x] ��
prime element.
[x] ��
prime element.
�ѳo�өw�q�ڭ̰��W�o��H�U�� Lemma.
Lemma 7.3.10
���]
p(
x)


[
x] �B
deg(
p(
x)) > 0.
- �Y p(x) �O�@�� irreducible element, �h p(x) �O�@�� primitive
polynomial.
- �Y p(x) �O�@�� prime element, �h p(x) �O�@�� primitive
polynomial.
�� ��.
(1) ���]
p(
x) �O irreducible. �]
p(
x) =
c(
p)
. p*(
x), �䤤
c(
p)




[
x] �B
p*(
x)


[
x], �ҥH
c(
p) �O
p(
x) ���@�� divisor. ��
p(
x) �O irreducible ��
deg(
p*(
x)) = deg(
p(
x)) > 0 ��
c(
p) = 1, �G�o
p(
x) �O primitive.
(2) ���] p(x) �O prime. �]
p(x) = c(p) . p*(x), �G��
p(x) | c(p) . p*(x). �� p(x) �O prime �����], ��
p(x) | c(p) ��
p(x) | p*(x). �ѩ�
deg(p(x)) > 0 �����i��
p(x) | c(p).
�G�o
p(x) | p*(x). �]�N�O���s�b
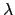 (x)
(x) 
 [x] �ϱo
p*(x) =
[x] �ϱo
p*(x) = 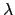 (x) . p(x). �G�o
p*(x) =
(x) . p(x). �G�o
p*(x) = 
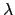 (x) . c(p)
(x) . c(p) . p*(x). �Q��
. p*(x). �Q��
 [x] �O integral domain ��
p*(x)
[x] �O integral domain ��
p*(x) 0 ��
0 ��
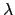 (x) . c(p) = 1. �]�N�O��
(x) . c(p) = 1. �]�N�O��
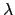 (x) �M
c(p) �O
(x) �M
c(p) �O
 [x] �� unit. ���ѩw�q c(p) �O�����, �G�o
[x] �� unit. ���ѩw�q c(p) �O�����, �G�o
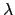 (x) = c(p) = 1. �]�N�O�� p(x) �O primitive.
(x) = c(p) = 1. �]�N�O�� p(x) �O primitive.

�p�e���X�`�������G, �ڭ̱N�|�ұo�b
 [x] ���� irreducible element
�M prime element �O�@�˪�. �ѩ�
[x] ���� irreducible element
�M prime element �O�@�˪�. �ѩ�
 [x] �S���Ҧ��� ideal ���O
principle ideal ���ʽ�, �ڭ̤���Ϋe������k�p�k�w�s. �ڭ̱N�Q��
[x] �S���Ҧ��� ideal ���O
principle ideal ���ʽ�, �ڭ̤���Ϋe������k�p�k�w�s. �ڭ̱N�Q��
 [x] ���� irreducible element ���ʽ�������B�z,
�ҥH�ڭ̻ݭn���F�Ѧb
[x] ���� irreducible element ���ʽ�������B�z,
�ҥH�ڭ̻ݭn���F�Ѧb
 [x] ���� irreducible element �M
[x] ���� irreducible element �M
 [x]
���� irreducible element ���������Y.
[x]
���� irreducible element ���������Y.
Lemma 7.3.11
�Y
p(
x)


[
x],
deg(
p(
x)) > 0 �B
p(
x) �O�@�� primitive
polynomial, �h
p(
x) �O

[
x] ���� irreducible element �Y�B�߭Y
p(
x) �O

[
x] ���� irreducible element.
�� ��.
�������]
p(
x) �O

[
x] ���� irreducible element. �p�G
p(
x) �b

[
x] �����O irreducible element, ���ܦs�b
g(
x),
h(
x)


[
x]
����
0 < deg(
g(
x)) < deg(
p(
x)),
0 < deg(
h(
x)) < deg(
p(
x)) �B
p(
x) =
g(
x)
. h(
x). �Q�� Lemma
7.3.8 ���s�b
m(
x),
n(
x)


[
x] �B
deg(
m(
x)) = deg(
g(
x)),
deg(
n(
x)) = deg(
h(
x)) ����
p(
x) =
m(
x)
. n(
x). �]�N�O��
m(
x)
�O
p(
x) �� divisor. ��
0 < deg(
m(
x)) < deg(
p(
x)), �G��
m(
x)

±1 �B
m(
x)

±
p(
x). ���M
p(
x) �O

[
x] ���@��
irreducible element ���]�ۥ٬�. �G��
p(
x) �]�O

[
x] ����
irreducible element.
�Ϥ�, �Y p(x) �O
 [x] ���� irreducible element. �Y
p(x) = m(x) . n(x), �䤤
m(x), n(x)
[x] ���� irreducible element. �Y
p(x) = m(x) . n(x), �䤤
m(x), n(x) 
 [x]. �� p(x) �b
[x]. �� p(x) �b
 [x] �O irreducible �����]�� m(x) �M n(x) �����@�ӬO
[x] �O irreducible �����]�� m(x) �M n(x) �����@�ӬO
 [x] �� unit, �Y�`��: �N���] m(x) = d �O�`�Ƨa! �]
m(x)
[x] �� unit, �Y�`��: �N���] m(x) = d �O�`�Ƨa! �]
m(x) 
 [x] �G��
d
[x] �G��
d 
 . ��
p(x) = d . n(x) �� d �O
p(x) ���Ҧ��Y�ƪ����]��. ���w�� p(x) �O primitive, �G�o d = ±1. �]�N�O�� p(x) �� divisor �u��O ±1 �M ±p(x)
�o�اΦ�, �G�o p(x) �b
. ��
p(x) = d . n(x) �� d �O
p(x) ���Ҧ��Y�ƪ����]��. ���w�� p(x) �O primitive, �G�o d = ±1. �]�N�O�� p(x) �� divisor �u��O ±1 �M ±p(x)
�o�اΦ�, �G�o p(x) �b
 [x] ���O irreducible.
[x] ���O irreducible.

�ѩ�
 �O�@�� field, �ҥH�W�@�`�� F[x] ���ʽ賣�i�M�Φb
�O�@�� field, �ҥH�W�@�`�� F[x] ���ʽ賣�i�M�Φb
 [x] �W. �ڭ̭n�Q��
[x] �W. �ڭ̭n�Q��
 [x] ���� irreducible �M prime �O�@�˪�,
�o��b
[x] ���� irreducible �M prime �O�@�˪�,
�o��b
 [x] ���� irreducible �M prime �]�O�@�˪�.
[x] ���� irreducible �M prime �]�O�@�˪�.
Proposition 7.3.12
���]
p(
x)


[
x]. �Y
p(
x) �O

[
x] ���� irreducible
element, �h
p(
x) �O

[
x] ���� prime element. �Ϥ�, �Y
p(
x)
�O

[
x] ���� prime element, �h
p(
x) �O

[
x] ����
irreducible element.
�� ��.
�����`�N, ��
deg(
p(
x)) = 0 �ɪ���
p(
x)


�O�@�ӱ`��.
�ڭ̤w���b

���� irreducible �M prime �O�@�˪� (Proposition
7.1.7), �ҥH�ڭ̥u�n����
deg(
p(
x)) > 0 �����p.
�������] p(x) �O
 [x] ���� irreducible element. �� Lemma
7.3.10 ���䬰 primitive, �G�� Lemma 7.3.11 �� p(x)
�]�O
[x] ���� irreducible element. �� Lemma
7.3.10 ���䬰 primitive, �G�� Lemma 7.3.11 �� p(x)
�]�O
 [x] ���� irreducible element. �A�� Proposition
7.2.11 �� p(x) �O
[x] ���� irreducible element. �A�� Proposition
7.2.11 �� p(x) �O
 [x] ���� prime element. ��Y
f (x), g(x)
[x] ���� prime element. ��Y
f (x), g(x) 
 [x] �B
p(x) | f (x) . g(x) in
[x] �B
p(x) | f (x) . g(x) in
 [x], ��
Lemma 7.3.7 ��
p(x) | f (x) . g(x) in
[x], ��
Lemma 7.3.7 ��
p(x) | f (x) . g(x) in
 [x]. �G��
p(x) �b
[x]. �G��
p(x) �b
 [x] �O prime �o
p(x) | f (x) ��
p(x) | g(x) in
[x] �O prime �o
p(x) | f (x) ��
p(x) | g(x) in
 [x]. �A�� Lemma 7.3.7 ��
p(x) | f (x) ��
p(x) | g(x) in
[x]. �A�� Lemma 7.3.7 ��
p(x) | f (x) ��
p(x) | g(x) in
 [x]. �]�N�O�� p(x) �O
[x]. �]�N�O�� p(x) �O
 [x] ���� prime element.
[x] ���� prime element.
�Ϥ�, �Y p(x) �O
 [x] ���� prime element. �Y
p(x) = m(x) . n(x) �䤤
m(x), n(x)
[x] ���� prime element. �Y
p(x) = m(x) . n(x) �䤤
m(x), n(x) 
 [x]. �h�ѩ�
p(x) | m(x) . n(x),
�i�o
p(x) | n(x) ��
p(x) | m(x). �Y
p(x) | n(x), �Y�s�b
[x]. �h�ѩ�
p(x) | m(x) . n(x),
�i�o
p(x) | n(x) ��
p(x) | m(x). �Y
p(x) | n(x), �Y�s�b
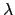 (x)
(x) 
 [x] �ϱo
n(x) =
[x] �ϱo
n(x) = 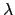 (x) . p(x). �G�o
(x) . p(x). �G�o
n(
x) =
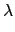
(
x)
. 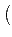 n
n(
x)
. m(
x)
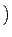
=
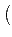
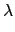
(
x)
. m(
x)
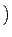 . n
. n(
x).
��
n(
x)

0 �H��

[
x] �O integral domain, �o
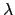
(
x)
. m(
x) = 1.
�]�N�O��
m(
x) �O

[
x] �� unit, �Y
m(
x) = ±1. �P�z, �Y
p(
x) |
m(
x) �i�o
n(
x) = ±1. �o��
p(
x) �� divisor ���O ±1 �M ±
p(
x) �o�اΦ�, �G��
p(
x) �O�@�� irreducible element.

��b�n�ҩ�
 [x] �W���ߤ@���ѩʽ��S�X�F�@�u�ƥ�,
�e���X�`���ڭ��ҩ��ߤ@���ѩʽ�èS���Ψ�C�@�� ideal ���O principle
ideal ���ʽ�, �ӬO�Ψ�p Proposition 7.3.12 ���C�� irreducible
element �O prime ���ʽ�. �p�P�b��ƪ����p, �ѩ� f (x) �M - f (x)
�����ѶȮt�@�ӥ��t��, �ڭ̥i�H�u�Ҽ�̰������Y�ƬO����ƪ�
polynomial.
[x] �W���ߤ@���ѩʽ��S�X�F�@�u�ƥ�,
�e���X�`���ڭ��ҩ��ߤ@���ѩʽ�èS���Ψ�C�@�� ideal ���O principle
ideal ���ʽ�, �ӬO�Ψ�p Proposition 7.3.12 ���C�� irreducible
element �O prime ���ʽ�. �p�P�b��ƪ����p, �ѩ� f (x) �M - f (x)
�����ѶȮt�@�ӥ��t��, �ڭ̥i�H�u�Ҽ�̰������Y�ƬO����ƪ�
polynomial.
Theorem 7.3.13
�Y
f (
x)


[
x] �O�@�Ӥ��� 0, 1, - 1 �B�̰������Y�ƬO����ƪ�
polynomial, �h�s�b
p1(
x),...,
pr(
x)


[
x], �䤤�o��
pi(
x)
�O

[
x] �����۲��B�̰������Y�ƬO����ƪ� irreducible elements,
����
f (
x) =
p1(
x)
n1 ... pr(
x)
nr,
ni 
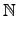
,
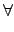 i
i 
{1,...,
r}.
�p�G f (x) �i�H���Ѧ��t� ���Φ�
f (x) = q1(x)m1 ... qs(x)ms, �䤤�o�� qi(x) �]�O
 [x]
�����۲��B�̰����Y�ƬO����ƪ� irreducible elements, �h r = s
�B�g�L�ܴ����ǥi�o
pi(x) = qi(x), ni = mi,
[x]
�����۲��B�̰����Y�ƬO����ƪ� irreducible elements, �h r = s
�B�g�L�ܴ����ǥi�o
pi(x) = qi(x), ni = mi,
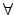 i
i  {1,..., r}.
{1,..., r}.
�� ��.
�����ҩ��s�b��, �]�N�O
f (
x) �i�g�������h��

[
x] ����
irreducible elements �����n. �ڭ̵̨M (�� degree)
�μƾ��k�Ǫk���ҩ�. ���]
deg(
f (
x)) = 0, �]
f (
x)


�B���O
unit, �G��

�����ѩʽ� (Theorem
7.1.8) ���s�b�ʪ�
f (
x)
�i�g�������h�� irreducible elements �����n. ����]�s�b�ʹ� degree
�p��
n �� polynomial �Ҧ���. ��
deg(
f (
x)) =
n ��, �Y
f (
x)
�����O irreducible, �s�b�ʦ۵M����. �G�ȳ�
f (
x) ���O irreducible
�����p�n�Ҽ. ���ɭn�`�N, �b

[
x] ���@�� polynomial �O
irreducible �ä����ܥL�@�w�i�H�g����� degree ����p�� polynomials
�����n (�Ҧp�e�����L���Ҥl 2
x + 2). ���ɧڭ̥��N
f (
x) �g��
f (
x) =
c(
f )
. f*(
x), �䤤
f*(
x)


[
x] �O primitive
polynomial. �ѩ�
c(
f )


, �A�@���Q�� Theorem
7.1.8 ��
c(
f )= 1 �άO�i�H�g�������h�� irreducible �`�� polynomials �����n.
�ҥH�ڭ̥u�ѤU�Ҽ
f*(
x) �O�_�i�g�������h�� irreducible elements
�����n. ��
f*(
x) �O irreducible ��, �s�b�ʦ۵M�S���ߤF. �ӷ�
f*(
x) ���O irreducible ��, Lemma
7.3.11 �i�D�ڭ�
f*(
x)
�b

[
x] ���O irreducible, �]�N�O
f*(
x) =
g(
x)
. h(
x) �䤤
g(
x),
h(
x)


[
x] �B
0 < deg(
g(
x)) < deg(
f (
x)) �H��
0 < deg(
h(
x)) < deg(
f (
x)). �� Lemma
7.3.8 ���s�b
m(
x),
n(
x)


[
x] �B
deg(
m(
x)) = deg(
g(
x)) �H��
deg(
n(
x)) = deg(
h(
x)) �ϱo
f*(
x) =
m(
x)
. n(
x). �ѩ�
deg(
m(
x)) < deg(
f (
x)) =
n �H��
deg(
n(
x)) <
n, �G�Q���k�Ǫk���]��
m(
x) �M
n(
x) ���i�g�������h�� irreducible elements �����n.
�]���o��
f*(
x) �i�H�g�������h�� irreducible elements �����n, �G��
f (
x) =
c(
f )
f*(
x) �]�i�g�������h�� irreducible elements �����n.
�ܩ�ߤ@�ʧڭ̵̨M�μƾ��k�Ǫk�ӳB�z. �Y
deg(f (x)) = 0, �]
f (x) 
 , �G�i�H�Q�� Theorem 7.1.8 ���ߤ@�ʱo�Ұߤ@��.
����]�ߤ@�ʹ� degree �p�� n �� polynomial �Ҧ���. ��
deg(f (x)) = n ��, �Y
, �G�i�H�Q�� Theorem 7.1.8 ���ߤ@�ʱo�Ұߤ@��.
����]�ߤ@�ʹ� degree �p�� n �� polynomial �Ҧ���. ��
deg(f (x)) = n ��, �Y
f (x) = p1(x)n1 ... pr(x)nr = q1(x)m1 ... qs(x)ms,
�䤤
pi(
x)
���۲�,
qj(
x) �]�O���۲�, �ӥB
pi(
x),
qj(
x) ���O

[
x]
���̰������Y�ƬO����ƪ� irreducible elements. �ѩ�
deg(
f (
x)) > 0,
�G��
pi(
x) �����s�b�@ polynomial �� degree �j�� 0,
�g���ƫ�ڭ̥O����
p1(
x). Proposition
7.3.12 �i�D�ڭ�
p1(
x) �O

[
x] �� prime element, �G��
p1(
x) |
f (
x) �o��,
qj(
x) �����@ polynomial �|�Q
p1(
x) �㰣, �g���ƫ�ڭ̥O����
q1(
x). �]�N�O��
p1(
x) |
q1(
x). �M��
q1(
x) �O
irreducible, �� divisor �u�� ±1 �M
±
q1(
x). �S�]�w��
deg(
p1(
x)) > 0 �B
p1(
x) �M
q1(
x) ���̰������Y�Ƴ��O�����,
�G�o
p1(
x) =
q1(
x). �]���ڭ̥i�N
f (
x) �����ѧ�g��
f (x) = p1(x)n1 . p2(x)n2 ... pr(x)nr = p1(x)m1 . q2(x)m2 ... qs(x)ms.
�N�W�������A���X
p1(
x), �ڭ̥i�o
p1(
x)
.  p1
p1(
x)
n1 - 1 . p2(
x)
n2 ... pr(
x)
nr -
p1(
x)
m1 - 1 . q2(
x)
m2 ... qs(
x)
ms
= 0.
�ѩ�
p1(
x)

0 �B

[
x] �O integral
domain, �ڭ̱o
p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr - p1(x)m1 - 1 . q2(x)m2 ... qs(x)ms = 0.
��O
g(
x) =
p1(
x)
n1 - 1 . p2(
x)
n2 ... pr(
x)
nr. �ѩ������
p1(
x) ����
deg(
p1(
x)) > 0, �G�o
deg(g(x)) = deg(f (x)) - deg(p1(x)) < deg(f (x)) = n
�B
g(x) = p1(x)n1 - 1 . p2(x)n2 ... pr(x)nr = p1(x)m1 - 1 . q2(x)m2 ... qs(x)ms
�O
g(
x) ����Ӥ���, �G�Q���k�Ǫk���]�ڭ̦�
r =
s �B
p1(
x) =
q1(
x),...,
pr(
x) =
qr(
x) �H��
n1 =
m1,
n2 =
m2,...,
nr =
mr, �G�o�Ұߤ@��.

�� Theorem 7.3.13 ��
 [x] ���� irreducible elements �N�p�P
[x] ���� irreducible elements �N�p�P
 ������Ƥ@�˭��n. �t�@�譱�Q�� Lemma 7.3.8 �]�i�D�ڭ̦b
������Ƥ@�˭��n. �t�@�譱�Q�� Lemma 7.3.8 �]�i�D�ڭ̦b
 [x] ���� irreducible element �b
[x] ���� irreducible element �b
 [x] ���]�O irreducible.
�]�����Q
[x] ���]�O irreducible.
�]�����Q
 [x] �������� irreducible elements �O�@�ӭ��n�����D.
��굹�w
f (x)
[x] �������� irreducible elements �O�@�ӭ��n�����D.
��굹�w
f (x) 
 [x] �n�P�_��O�_�� irreducible ��e��.
�H�U�ڭ̤��Ф@�ؤ�k�i�H�T��Y�@���� polynomial �O irreducible.
[x] �n�P�_��O�_�� irreducible ��e��.
�H�U�ڭ̤��Ф@�ؤ�k�i�H�T��Y�@���� polynomial �O irreducible.
Proposition 7.3.14 (Eisenstein Criterion)
�O
f (
x) =
xn +
an - 1xn - 1 +
... +
a1x +
a0 

[
x],
�䤤
n > 0.
���]�s�b�@���
p 

����
p |
a0,
p |
a1, ...,
p |
an - 1 ��
p2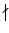 a0
a0,
�h
f (
x) �O

[
x] ���� irreducible element.
�� ��.
�ѩ�
c(
f )= 1 �ҥH
f (
x) �O primitive polynomial. �]���n����
f (
x)
�O irreducible in

[
x] �u�n����
f (
x) ���i��g����� degree
�p��
n �� polynomials �����n. �ڭ̧Q�Τ��Ҫk���ҩ�.
���]
f (x) = g(x) . h(x) �䤤
g(
x) =
crxr +
... +
c1x +
c0 

[
x], 0 <
r <
n
�B
h(
x) =
dsxs +
... +
d1x +
d0 

[
x], 0 <
s <
n.
�Ҽ
g(
x)
. h(
x) ���`�ƶ�
c0 . d0 =
a0. �Ѱ��]
p |
a0 =
c0 . d0, �G��
p |
c0 ��
p |
d0. �M�ӤS��
p2 c0 . d0
c0 . d0, �G��
c0 �M
d0 ���u��@�ӳQ
p
�㰣. �ڭ̴N���]�O
c0 �a! �]�N�O��
p |
c0 ��
p d0
d0. ��b�[��
g(
x)
. h(
x) ���@�����Y��
c0 . d1 +
c1 . d0 =
a1. �Ѱ��]
p |
a1 �H�� �o����
p |
c0 �i�o
p |
c1 . d0. ���S��
p d0
d0 �G�o
p |
c1.
�o�ˤ@���U�h�ڭ̷Q�μƾ��k�Ǫk�ұo
p |
cr. �]�N�O���]�w��
p |
c0,
p |
c1,...,
p |
cr - 1, �ڭ̱��ұo
p |
cr.
��Ҽ
g(
x)
. h(
x) ��
xr ���Y��
c0 . dr + c1 . dr - 1 + ... + cr - 1 . d1 + cr . d0 = ar.
(�o�Ӧ��l�̭Y
s <
r, �����M�O�O
ds + 1 =
... =
dr = 0) �ѩ� 0 <
r <
n �G��
p |
ar, �A�[�W�k�ǰ��]
p |
c0,...,
p |
cr - 1, �ڭ̥i�o
p |
cr . d0. �O�ѤF
p d0
d0, �G�o��
p |
cr.
��b�ڭ̦Ҽ
g(
x)
. h(
x) ���̰������Y�� (�Y
f (
x) ��
xn
���Y��)
cr . ds = 1.
�j�a���W�ݥX��
p |
cr ���i��o��
cr . ds = 1.
�]���o��٬�, �]�N�O��
f (
x) �O

[
x] �� irreducible element.

�̫�ڭ̭��Ӥ@�U, �� Lemma 7.3.8 (�� Lemma 7.3.11)
�ڭ̪��D�ŦX Proposition 7.3.14 �� polynomials �b
 [x] �]�O
irreducible.
[x] �]�O
irreducible.



�U�@��: Quotient Field of an
�W�@��: �@�DZ`���� Rings
�e�@��: Ring of Polynomials over
Administrator
2005-06-18
![]() [x] ���ܩҦ����z�Y�� polynomials �Ҧ������X�B�O
[x] ���ܩҦ����z�Y�� polynomials �Ҧ������X�B�O
![]() [x]
���ܩҦ���Y�� polynomials �Ҧ������X. �e���w��
[x]
���ܩҦ���Y�� polynomials �Ҧ������X. �e���w��
![]() [x]
�Τ@�몺�[�k�M���k�i�Φ��@�� ring, �ڭ̺٤��� polynomial ring over
[x]
�Τ@�몺�[�k�M���k�i�Φ��@�� ring, �ڭ̺٤��� polynomial ring over
![]() . �P�z�ڭ̤]�i�H�ҥX
. �P�z�ڭ̤]�i�H�ҥX
![]() [x] �]�O�@�� ring, �ڭ̺٤���
polynomial ring over
[x] �]�O�@�� ring, �ڭ̺٤���
polynomial ring over
![]() .
.
![]() [x] �� 0 �M 1 �M
[x] �� 0 �M 1 �M
![]() [x] �� 0 �M 1 �ۦP. �ڭ̤]�i�b
[x] �� 0 �M 1 �ۦP. �ڭ̤]�i�b
![]() [x] ���w�q degree (�ϥ��i�H��
[x] ���w�q degree (�ϥ��i�H��
![]() [x] �ݦ�
[x] �ݦ�
![]() [x] ���l���X).
�ҥH�Q�ΩM Lemma 7.2.3 �ۦP���ҩ�, �ڭ̥i�o
[x] ���l���X).
�ҥH�Q�ΩM Lemma 7.2.3 �ۦP���ҩ�, �ڭ̥i�o
![]() [x] �O�@��
integral domain.
[x] �O�@��
integral domain.
![]() [x] �M
[x] �M
![]() [x] �̤j�����P�O
[x] �̤j�����P�O
![]() [x] ���Ҧ��D
0 ���`�Ƴ��O unit, �M��
[x] ���Ҧ��D
0 ���`�Ƴ��O unit, �M��
![]() [x] ���u�� ±1 �o��ӱ`�Ƭ���
unit. �o�O�]���Q�� Lemma 7.2.3 ���ҩ��ڭ̪��D
[x] ���u�� ±1 �o��ӱ`�Ƭ���
unit. �o�O�]���Q�� Lemma 7.2.3 ���ҩ��ڭ̪��D
![]() [x] ����
unit �� degree �@�w�O 0, �ҥH�u���`�Ƥ �i��O
[x] ����
unit �� degree �@�w�O 0, �ҥH�u���`�Ƥ �i��O
![]() [x] �� unit,
�M�Ӧ]�ڭ̥u�Ҽ��Y��, �ҥH�b
[x] �� unit,
�M�Ӧ]�ڭ̥u�Ҽ��Y��, �ҥH�b
![]() ���� unit � �i�H�O
���� unit � �i�H�O
![]() [x] ��
unit, �]�N�O ±1. �]���o�̧ڭ̥��������j�a, �b
[x] ��
unit, �]�N�O ±1. �]���o�̧ڭ̥��������j�a, �b
![]() [x]
���ͤ��Ѯɭn�N�`�ƪ����ѦC�J�Ҽ.
[x]
���ͤ��Ѯɭn�N�`�ƪ����ѦC�J�Ҽ.
![]() [x] ���èS���l���w�z,
�ҥH�b
[x] ���èS���l���w�z,
�ҥH�b
![]() [x] ���i�Q�ξl���w�z�o�쪺�Ҧ� ideal ���O principle
ideal (Theorem 7.2.6) ��
[x] ���i�Q�ξl���w�z�o�쪺�Ҧ� ideal ���O principle
ideal (Theorem 7.2.6) ��
![]() [x] �N���@�w��.
�ƹ�W�ڭ̥i�H�b
[x] �N���@�w��.
�ƹ�W�ڭ̥i�H�b
![]() [x] �����@�� (���M���u�@��) ideal �����O
principle ideal.
[x] �����@�� (���M���u�@��) ideal �����O
principle ideal.
![]() [x] ���� ideal ���@�w�O principle ideal
����ڭ̴N����� Proposition 7.2.11 ����k�o��
[x] ���� ideal ���@�w�O principle ideal
����ڭ̴N����� Proposition 7.2.11 ����k�o��
![]() [x] ����
irreducible element �N�O prime element �F.
����γo�M��k�ä����ܵ��G�|��,
�]�����i��Υt�@�M��k�i�H�o��Q�n�����G��!
�S���ڭ̱N�|�ҩ��b
[x] ����
irreducible element �N�O prime element �F.
����γo�M��k�ä����ܵ��G�|��,
�]�����i��Υt�@�M��k�i�H�o��Q�n�����G��!
�S���ڭ̱N�|�ҩ��b
![]() [x] ���� irreducible element �M prime
element �O�ۦP��, ���L�ڭ̭n�o�i�t�@�M����k�ӱo��.
[x] ���� irreducible element �M prime
element �O�ۦP��, ���L�ڭ̭n�o�i�t�@�M����k�ӱo��.
![]() [x] �M
[x] �M
![]() [x] �̤j�����P�N�O�b
[x] �̤j�����P�N�O�b
![]() [x] ���n�Ҽ�`�ƪ�����. ���w
f (x) = a0 + a1x + ... + anxn
[x] ���n�Ҽ�`�ƪ�����. ���w
f (x) = a0 + a1x + ... + anxn ![]()
![]() [x] �n�N f (x) ���Ѧ� degree ����p�� polynomials
�ۭ����e, �i�H���Ҽ�i���i�H���X�@�ӱ`�ƥX�� (�]���Y�o�ӱ`�Ƥ��O
±1 ����b
[x] �n�N f (x) ���Ѧ� degree ����p�� polynomials
�ۭ����e, �i�H���Ҽ�i���i�H���X�@�ӱ`�ƥX�� (�]���Y�o�ӱ`�Ƥ��O
±1 ����b
![]() [x] ���o�N��O�@��``����''������).
�i�H���X�ƻ�`�ƥX�өO? �j�a���|�Q�촣�X���ǫY��
a0, a1,..., an
���̤j���]�Ƨa! �ҥH�ڭ̦��H�U²������n�����G.
[x] ���o�N��O�@��``����''������).
�i�H���X�ƻ�`�ƥX�өO? �j�a���|�Q�촣�X���ǫY��
a0, a1,..., an
���̤j���]�Ƨa! �ҥH�ڭ̦��H�U²������n�����G.
![]()
![]() �B
f*(x)
�B
f*(x) ![]()
![]() [x]. �N c ���J f*(x) ���U���Y�Ƥ�, �� f (x)
���Ҧ��Y��
a0, a1,..., an ���|�O c ������. �]�N�O c �O
a0, a1,..., an �����]��. �p�G
c
[x]. �N c ���J f*(x) ���U���Y�Ƥ�, �� f (x)
���Ҧ��Y��
a0, a1,..., an ���|�O c ������. �]�N�O c �O
a0, a1,..., an �����]��. �p�G
c![]() d = gcd(a0, a1,..., an),
�h f*(x) ���Y�Ƥ��|�� d /c �o�@�Ӥ��O 1 �����]��, ���M
f*(x) ���U���Y�ƪ��̤j���]�Ƭ� 1 �ۥ٬�. �G�o d = c, �]�N�O��
d . f*(x) = d . (b0 + b1x + ... + bnxn). �̫�]
d = gcd(a0, a1,..., an),
�h f*(x) ���Y�Ƥ��|�� d /c �o�@�Ӥ��O 1 �����]��, ���M
f*(x) ���U���Y�ƪ��̤j���]�Ƭ� 1 �ۥ٬�. �G�o d = c, �]�N�O��
d . f*(x) = d . (b0 + b1x + ... + bnxn). �̫�]
![]() [x] �O
integral domain, �ڭ̱o
f*(x) = b0 + b1x + ... + bnxn.
[x] �O
integral domain, �ڭ̱o
f*(x) = b0 + b1x + ... + bnxn.
![]()
![]()
![]() [x] ���i�H�g���� content ���W�@��
primitive polynomial. �ڭ̥i�H�N Lemma 7.3.2 ���s��
[x] ���i�H�g���� content ���W�@��
primitive polynomial. �ڭ̥i�H�N Lemma 7.3.2 ���s��
![]() [x]
��.
[x]
��.
![]()
![]() [x] ���O primitive polynomials.
�N d �M d' ���O�g�� a/b �M a'/b', �䤤
a, a', b, b'
[x] ���O primitive polynomials.
�N d �M d' ���O�g�� a/b �M a'/b', �䤤
a, a', b, b' ![]()
![]() .
�ڭ̥i�o
.
�ڭ̥i�o
![]() [x],
�H��ڭ̱N�|����N��
f (x)
[x],
�H��ڭ̱N�|����N��
f (x) ![]()
![]() [x] �g��
f (x) = c(f ) . f*(x),
�䤤
0 < c(f )
[x] �g��
f (x) = c(f ) . f*(x),
�䤤
0 < c(f ) ![]()
![]() �O f (x) �� content,
f*(x)
�O f (x) �� content,
f*(x) ![]()
![]() [x] �O�@��
primitive polynomial.
[x] �O�@��
primitive polynomial.
![]()
![]() [x], �n�p��
f (x) . g(x) �� content,
���O�ܽ�����. �ڭ̥������� polynomial ���, ������z,
�A�q����̤j���]��. �ڭ̷��M�Ʊ�
f (x) . g(x) �� content �i�H��
f (x) �M g(x) �� contents �����D�X�N�n�F.
���ڭ̥��ݤ@�ӯS���Ҥl�N�O f (x) �M g(x) �� contents ���O 1
�����p.
[x], �n�p��
f (x) . g(x) �� content,
���O�ܽ�����. �ڭ̥������� polynomial ���, ������z,
�A�q����̤j���]��. �ڭ̷��M�Ʊ�
f (x) . g(x) �� content �i�H��
f (x) �M g(x) �� contents �����D�X�N�n�F.
���ڭ̥��ݤ@�ӯS���Ҥl�N�O f (x) �M g(x) �� contents ���O 1
�����p.
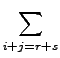 ai . bj.
ai . bj.
![]()
![]() [x],
�ڭ̫ܧ֪��N�i�H�p��X
c(f . g).
[x],
�ڭ̫ܧ֪��N�i�H�p��X
c(f . g).
![]() [x] �W������, �����n�Ϥ��@�U�b
[x] �W������, �����n�Ϥ��@�U�b
![]() [x] �M
[x] �M
![]() [x] �����㰣����. ���w
f (x), g(x)
[x] �����㰣����. ���w
f (x), g(x) ![]()
![]() [x], �ڭ̻�
f (x) | g(x) in
[x], �ڭ̻�
f (x) | g(x) in
![]() [x] ���ܦs�b
h(x)
[x] ���ܦs�b
h(x) ![]()
![]() [x] ����
g(x) = h(x) . f (x). �ӧڭ̻�
f (x) | g(x) in
[x] ����
g(x) = h(x) . f (x). �ӧڭ̻�
f (x) | g(x) in
![]() [x] ���ܦs�b
l (x)
[x] ���ܦs�b
l (x) ![]()
![]() [x]
����
g(x) = l (x) . f (x). �o�̳̤j�����P�b�� h(x) �n�D���b
[x]
����
g(x) = l (x) . f (x). �o�̳̤j�����P�b�� h(x) �n�D���b
![]() [x], �� l (x) �n�b
[x], �� l (x) �n�b
![]() [x] �Y�i. �ҥH���i��o��
f (x) | g(x) in
[x] �Y�i. �ҥH���i��o��
f (x) | g(x) in
![]() [x] ��
f (x)
[x] ��
f (x)![]() g(x) in
g(x) in
![]() [x] �����p.
[x] �����p.
![]() [x], ���ܦs�b
l (x)
[x], ���ܦs�b
l (x) ![]()
![]() [x] ����
g(x) = l (x) . f (x). �ڭ̧Ʊ���ұo
l (x)
[x] ����
g(x) = l (x) . f (x). �ڭ̧Ʊ���ұo
l (x) ![]()
![]() [x]. �Q�� Lemma
7.3.4 �N l (x) �g��
l (x) = c(l ) . l*(x), �䤤 l*(x) �O
primitive polynomials. �G�o
g(x) = c(l ) . (l*(x) . f (x)). �]��
f (x) �M l*(x) ���O primitive polynomials, �G�Q�� Lemma
7.3.5 ��
l*(x) . f (x) �O primitive polynomial. �A�Q��
Lemma 7.3.4 ���ߤ@�ʪ� c(g) = c(l ). �]
c(g)
[x]. �Q�� Lemma
7.3.4 �N l (x) �g��
l (x) = c(l ) . l*(x), �䤤 l*(x) �O
primitive polynomials. �G�o
g(x) = c(l ) . (l*(x) . f (x)). �]��
f (x) �M l*(x) ���O primitive polynomials, �G�Q�� Lemma
7.3.5 ��
l*(x) . f (x) �O primitive polynomial. �A�Q��
Lemma 7.3.4 ���ߤ@�ʪ� c(g) = c(l ). �]
c(g) ![]()
![]() , �G�o
c(l )
, �G�o
c(l ) ![]()
![]() , �B�S
l*(x)
, �B�S
l*(x) ![]()
![]() [x], �G��
l (x) = c(l ) . l*(x)
�o
l (x)
[x], �G��
l (x) = c(l ) . l*(x)
�o
l (x) ![]()
![]() [x].
[x].
![]()
![]() [x] �M
[x] �M
![]() [x] �����Ѫ����P. �Y
f (x)
[x] �����Ѫ����P. �Y
f (x) ![]()
![]() [x] �ڭ̻� f (x) �b
[x] �ڭ̻� f (x) �b
![]() [x] �i���Ѫ��� f (x) �i�g��
f (x) = g(x) . h(x), �䤤
g(x), h(x)
[x] �i���Ѫ��� f (x) �i�g��
f (x) = g(x) . h(x), �䤤
g(x), h(x) ![]()
![]() [x] �B
deg(g(x)) �M
deg(h(x)) �Ҥp��
deg(f (x)). ���o����� f (x) �i�H�b
[x] �B
deg(g(x)) �M
deg(h(x)) �Ҥp��
deg(f (x)). ���o����� f (x) �i�H�b
![]() [x] �����Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x)
[x] �����Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x) ![]()
![]() [x].
���L�U�@�� Lemma �i�D�ڭ̳o�O��o�쪺.
[x].
���L�U�@�� Lemma �i�D�ڭ̳o�O��o�쪺.
![]() [x] �i�H���Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x)
[x] �i�H���Ѧ�
f (x) = m(x) . n(x), �䤤
m(x), n(x) ![]()
![]() [x], �B m(x), n(x) ���O
[x], �B m(x), n(x) ���O
![]() [x] ���� unit. ����
�j�a�@�w����ѩ� m(x), n(x) �]�b
[x] ���� unit. ����
�j�a�@�w����ѩ� m(x), n(x) �]�b
![]() [x] ���ҥH f (x) �b
[x] ���ҥH f (x) �b
![]() [x]
���i�H����. ��ꤣ�M, �]�� m(x), n(x) �b
[x]
���i�H����. ��ꤣ�M, �]�� m(x), n(x) �b
![]() [x] �����O unit,
���i��b
[x] �����O unit,
���i��b
![]() [x] ���N�O unit �F. �Ҧp 2x + 2 �b
[x] ���N�O unit �F. �Ҧp 2x + 2 �b
![]() [x] �O
irreducible ���b
[x] �O
irreducible ���b
![]() [x] ��
2x + 2 = 2 . (x + 1), �ӥB 2 �M x + 1
�b
[x] ��
2x + 2 = 2 . (x + 1), �ӥB 2 �M x + 1
�b
![]() [x] �������O unit (�� 2 �b
[x] �������O unit (�� 2 �b
![]() [x] �O unit), �ҥH 2x + 2
�b
[x] �O unit), �ҥH 2x + 2
�b
![]() [x] �ä��O irreducible. �q�o�̬ݥX
[x] �ä��O irreducible. �q�o�̬ݥX
![]() [x] ���� irreducible
element �M
[x] ���� irreducible
element �M
![]() [x] �� irreducible element ���P.
[x] �� irreducible element ���P.
![]() [x] ���� unit �u��
1 �M -1 �ҥH�ڭ̦��H�U���w�q.
[x] ���� unit �u��
1 �M -1 �ҥH�ڭ̦��H�U���w�q.
![]() (x)
(x) ![]()
![]() [x] �ϱo
p*(x) =
[x] �ϱo
p*(x) = ![]() (x) . p(x). �G�o
p*(x) =
(x) . p(x). �G�o
p*(x) = ![]()
![]() (x) . c(p)
(x) . c(p)![]() . p*(x). �Q��
. p*(x). �Q��
![]() [x] �O integral domain ��
p*(x)
[x] �O integral domain ��
p*(x)![]() 0 ��
0 ��
![]() (x) . c(p) = 1. �]�N�O��
(x) . c(p) = 1. �]�N�O��
![]() (x) �M
c(p) �O
(x) �M
c(p) �O
![]() [x] �� unit. ���ѩw�q c(p) �O�����, �G�o
[x] �� unit. ���ѩw�q c(p) �O�����, �G�o
![]() (x) = c(p) = 1. �]�N�O�� p(x) �O primitive.
(x) = c(p) = 1. �]�N�O�� p(x) �O primitive.
![]()
![]() [x] ���� irreducible element
�M prime element �O�@�˪�. �ѩ�
[x] ���� irreducible element
�M prime element �O�@�˪�. �ѩ�
![]() [x] �S���Ҧ��� ideal ���O
principle ideal ���ʽ�, �ڭ̤���Ϋe������k�p�k�w�s. �ڭ̱N�Q��
[x] �S���Ҧ��� ideal ���O
principle ideal ���ʽ�, �ڭ̤���Ϋe������k�p�k�w�s. �ڭ̱N�Q��
![]() [x] ���� irreducible element ���ʽ�������B�z,
�ҥH�ڭ̻ݭn���F�Ѧb
[x] ���� irreducible element ���ʽ�������B�z,
�ҥH�ڭ̻ݭn���F�Ѧb
![]() [x] ���� irreducible element �M
[x] ���� irreducible element �M
![]() [x]
���� irreducible element ���������Y.
[x]
���� irreducible element ���������Y.
![]() [x] ���� irreducible element. �Y
p(x) = m(x) . n(x), �䤤
m(x), n(x)
[x] ���� irreducible element. �Y
p(x) = m(x) . n(x), �䤤
m(x), n(x) ![]()
![]() [x]. �� p(x) �b
[x]. �� p(x) �b
![]() [x] �O irreducible �����]�� m(x) �M n(x) �����@�ӬO
[x] �O irreducible �����]�� m(x) �M n(x) �����@�ӬO
![]() [x] �� unit, �Y�`��: �N���] m(x) = d �O�`�Ƨa! �]
m(x)
[x] �� unit, �Y�`��: �N���] m(x) = d �O�`�Ƨa! �]
m(x) ![]()
![]() [x] �G��
d
[x] �G��
d ![]()
![]() . ��
p(x) = d . n(x) �� d �O
p(x) ���Ҧ��Y�ƪ����]��. ���w�� p(x) �O primitive, �G�o d = ±1. �]�N�O�� p(x) �� divisor �u��O ±1 �M ±p(x)
�o�اΦ�, �G�o p(x) �b
. ��
p(x) = d . n(x) �� d �O
p(x) ���Ҧ��Y�ƪ����]��. ���w�� p(x) �O primitive, �G�o d = ±1. �]�N�O�� p(x) �� divisor �u��O ±1 �M ±p(x)
�o�اΦ�, �G�o p(x) �b
![]() [x] ���O irreducible.
[x] ���O irreducible.
![]()
![]() �O�@�� field, �ҥH�W�@�`�� F[x] ���ʽ賣�i�M�Φb
�O�@�� field, �ҥH�W�@�`�� F[x] ���ʽ賣�i�M�Φb
![]() [x] �W. �ڭ̭n�Q��
[x] �W. �ڭ̭n�Q��
![]() [x] ���� irreducible �M prime �O�@�˪�,
�o��b
[x] ���� irreducible �M prime �O�@�˪�,
�o��b
![]() [x] ���� irreducible �M prime �]�O�@�˪�.
[x] ���� irreducible �M prime �]�O�@�˪�.
![]() [x] ���� irreducible element. �� Lemma
7.3.10 ���䬰 primitive, �G�� Lemma 7.3.11 �� p(x)
�]�O
[x] ���� irreducible element. �� Lemma
7.3.10 ���䬰 primitive, �G�� Lemma 7.3.11 �� p(x)
�]�O
![]() [x] ���� irreducible element. �A�� Proposition
7.2.11 �� p(x) �O
[x] ���� irreducible element. �A�� Proposition
7.2.11 �� p(x) �O
![]() [x] ���� prime element. ��Y
f (x), g(x)
[x] ���� prime element. ��Y
f (x), g(x) ![]()
![]() [x] �B
p(x) | f (x) . g(x) in
[x] �B
p(x) | f (x) . g(x) in
![]() [x], ��
Lemma 7.3.7 ��
p(x) | f (x) . g(x) in
[x], ��
Lemma 7.3.7 ��
p(x) | f (x) . g(x) in
![]() [x]. �G��
p(x) �b
[x]. �G��
p(x) �b
![]() [x] �O prime �o
p(x) | f (x) ��
p(x) | g(x) in
[x] �O prime �o
p(x) | f (x) ��
p(x) | g(x) in
![]() [x]. �A�� Lemma 7.3.7 ��
p(x) | f (x) ��
p(x) | g(x) in
[x]. �A�� Lemma 7.3.7 ��
p(x) | f (x) ��
p(x) | g(x) in
![]() [x]. �]�N�O�� p(x) �O
[x]. �]�N�O�� p(x) �O
![]() [x] ���� prime element.
[x] ���� prime element.
![]() [x] ���� prime element. �Y
p(x) = m(x) . n(x) �䤤
m(x), n(x)
[x] ���� prime element. �Y
p(x) = m(x) . n(x) �䤤
m(x), n(x) ![]()
![]() [x]. �h�ѩ�
p(x) | m(x) . n(x),
�i�o
p(x) | n(x) ��
p(x) | m(x). �Y
p(x) | n(x), �Y�s�b
[x]. �h�ѩ�
p(x) | m(x) . n(x),
�i�o
p(x) | n(x) ��
p(x) | m(x). �Y
p(x) | n(x), �Y�s�b
![]() (x)
(x) ![]()
![]() [x] �ϱo
n(x) =
[x] �ϱo
n(x) = ![]() (x) . p(x). �G�o
(x) . p(x). �G�o
![]() [x] �W���ߤ@���ѩʽ��S�X�F�@�u�ƥ�,
�e���X�`���ڭ��ҩ��ߤ@���ѩʽ�èS���Ψ�C�@�� ideal ���O principle
ideal ���ʽ�, �ӬO�Ψ�p Proposition 7.3.12 ���C�� irreducible
element �O prime ���ʽ�. �p�P�b��ƪ����p, �ѩ� f (x) �M - f (x)
�����ѶȮt�@�ӥ��t��, �ڭ̥i�H�u�Ҽ�̰������Y�ƬO����ƪ�
polynomial.
[x] �W���ߤ@���ѩʽ��S�X�F�@�u�ƥ�,
�e���X�`���ڭ��ҩ��ߤ@���ѩʽ�èS���Ψ�C�@�� ideal ���O principle
ideal ���ʽ�, �ӬO�Ψ�p Proposition 7.3.12 ���C�� irreducible
element �O prime ���ʽ�. �p�P�b��ƪ����p, �ѩ� f (x) �M - f (x)
�����ѶȮt�@�ӥ��t��, �ڭ̥i�H�u�Ҽ�̰������Y�ƬO����ƪ�
polynomial.
![]() [x]
�����۲��B�̰����Y�ƬO����ƪ� irreducible elements, �h r = s
�B�g�L�ܴ����ǥi�o
pi(x) = qi(x), ni = mi,
[x]
�����۲��B�̰����Y�ƬO����ƪ� irreducible elements, �h r = s
�B�g�L�ܴ����ǥi�o
pi(x) = qi(x), ni = mi,
![]() i
i ![]() {1,..., r}.
{1,..., r}.![]()
![]() , �G�i�H�Q�� Theorem 7.1.8 ���ߤ@�ʱo�Ұߤ@��.
����]�ߤ@�ʹ� degree �p�� n �� polynomial �Ҧ���. ��
deg(f (x)) = n ��, �Y
, �G�i�H�Q�� Theorem 7.1.8 ���ߤ@�ʱo�Ұߤ@��.
����]�ߤ@�ʹ� degree �p�� n �� polynomial �Ҧ���. ��
deg(f (x)) = n ��, �Y
![]() [x] ���� irreducible elements �N�p�P
[x] ���� irreducible elements �N�p�P
![]() ������Ƥ@�˭��n. �t�@�譱�Q�� Lemma 7.3.8 �]�i�D�ڭ̦b
������Ƥ@�˭��n. �t�@�譱�Q�� Lemma 7.3.8 �]�i�D�ڭ̦b
![]() [x] ���� irreducible element �b
[x] ���� irreducible element �b
![]() [x] ���]�O irreducible.
�]�����Q
[x] ���]�O irreducible.
�]�����Q
![]() [x] �������� irreducible elements �O�@�ӭ��n�����D.
��굹�w
f (x)
[x] �������� irreducible elements �O�@�ӭ��n�����D.
��굹�w
f (x) ![]()
![]() [x] �n�P�_��O�_�� irreducible ��e��.
�H�U�ڭ̤��Ф@�ؤ�k�i�H�T��Y�@���� polynomial �O irreducible.
[x] �n�P�_��O�_�� irreducible ��e��.
�H�U�ڭ̤��Ф@�ؤ�k�i�H�T��Y�@���� polynomial �O irreducible.
![]() [x] �]�O
irreducible.
[x] �]�O
irreducible.