


¤U¤@¶: Integral Domain ¤WŞş¤Ŕ¸Ń©Ę˝č
¤W¤@¶: ¤@¨Ç±`¨ŁŞş Rings
«e¤@¶: Polynomials over the Integers
Quotient Field of an Integral Domain
§ÚĚłŁŞľąD
 ¬O integral domain ¦Ó
¬O integral domain ¦Ó
 ¬O field. ¨Ćąę¤W
¬O field. ¨Ćąę¤W
 ¬OĄ]§t
¬OĄ]§t
 łĚ¤pŞş field. §Ú̱N±ŔĽs±q
łĚ¤pŞş field. §Ú̱N±ŔĽs±q
 «ŘşcĄX
«ŘşcĄX
 Şş¤čŞk¨ěĄô·NŞş integral domain D.
Şş¤čŞk¨ěĄô·NŞş integral domain D.
µą©wĄô·NŞş integral domain D, ĄO
S = {(a, b) | a, b  D, b
D, b 0}. şĄý§Ú̱N¦b S ¤¤©w¤@Ó equivalence relation. ąď©ó S
¤¤Şş¨â¤¸ŻŔ
(a, b),(c, d )
0}. şĄý§Ú̱N¦b S ¤¤©w¤@Ó equivalence relation. ąď©ó S
¤¤Şş¨â¤¸ŻŔ
(a, b),(c, d )  S, §ÚĚĄO
S, §ÚĚĄO
(
a,
b)
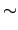
(
c,
d ) YĄB°ßY
a . d =
c . b.
 ¤¤ŞşĄô·N¤¸ŻŔYĄiĽg¦¨ a/b
¤Î c/d, ¨ä¤¤
a, b, c, d
¤¤ŞşĄô·N¤¸ŻŔYĄiĽg¦¨ a/b
¤Î c/d, ¨ä¤¤
a, b, c, d 
 ĄB
b
ĄB
b 0, d
0, d 0, ¨ş»ň¦ŰµM¦ł
a . d = c . b ło¤@ÓĂö«Y¦ˇ.
0, ¨ş»ň¦ŰµM¦ł
a . d = c . b ło¤@ÓĂö«Y¦ˇ.
§ÚĚnĹçĂŇ  ło¤@Ó relation ¬O¤@Ó equivalence relation:
ło¤@Ó relation ¬O¤@Ó equivalence relation:
- (equiv1)
- ąď©Ň¦łŞş
(a, b)
 S, ĄŃ©ó D ¬O¤@Ó integral domain ©ŇĄH commutative, ¬GŞľ
a . b = b . a. ©ŇĄH±oĂŇ
(a, b)
S, ĄŃ©ó D ¬O¤@Ó integral domain ©ŇĄH commutative, ¬GŞľ
a . b = b . a. ©ŇĄH±oĂŇ
(a, b)  (a, b).
(a, b).
- (equiv2)
- Y¤wŞľ
(a, b)
 (c, d ), §ÚĚ·QnĂұo
(c, d )
(c, d ), §ÚĚ·QnĂұo
(c, d )  (a, b). ĄŃ
(a, b)
(a, b). ĄŃ
(a, b)  (c, d ) §Ú̦ł
a . d = c . b
ło¤@ÓĂö«Y¦ˇ. ¦ÓnĂұo
(c, d )
(c, d ) §Ú̦ł
a . d = c . b
ło¤@ÓĂö«Y¦ˇ. ¦ÓnĂұo
(c, d )  (a, b) §ÚĚĄ˛¶·n¦ł
c . b = a . d, ¦ýło©M°˛ł]ŞşĂö«Y¦ˇ¬Ű¦P, ¬G±o
(c, d )
(a, b) §ÚĚĄ˛¶·n¦ł
c . b = a . d, ¦ýło©M°˛ł]ŞşĂö«Y¦ˇ¬Ű¦P, ¬G±o
(c, d )  (a, b).
(a, b).
- (equiv3)
- Y¤wŞľ
(a, b)
 (c, d ) ĄB
(c, d )
(c, d ) ĄB
(c, d )  (e, f ),
§Ú̧ƱćĂұo
(a, b)
(e, f ),
§Ú̧ƱćĂұo
(a, b)  (e, f ). ĄŃ°˛ł]±řĄó§Ú̦ł
(e, f ). ĄŃ°˛ł]±řĄó§Ú̦ł
| a . d |
= |
c . b |
(7.1) |
| c . f |
= |
e . d |
(7.2) |
n¦p¦ó±qĄH¤W (7.1) ©M (7.2) ¨âÓĂö«Y¦ˇ±o¨ě
a . f = e . b łoÓĂö«Y¦ˇ©O? şĄý±N¦ˇ¤l (7.1) ŞşµĄ¦ˇ¨âĂ伤W f,
±o
(a . d ) . f = (c . b) . f = (c . f ) . b.
¦A§QĄÎ¦ˇ¤l (7.2) ±o
(a . d ) . f = (e . d ) . b,
¤]´N¬O
d . (a . f - e . b) = 0. ¦] d 0, ĄB D ¨S¦ł zero
divisor (§O§Ń¤F D ¬O integral domain), ¬G±o
a . f = e . b.
0, ĄB D ¨S¦ł zero
divisor (§O§Ń¤F D ¬O integral domain), ¬G±o
a . f = e . b.
¦n¤F, ¬JµM  ¬O S ¤¤Şş¤@Ó equivalence relation, §ÚĚ´NĄiĄH±N
S ¤¤Şş¤¸ŻŔ§QĄÎ
¬O S ¤¤Şş¤@Ó equivalence relation, §ÚĚ´NĄiĄH±N
S ¤¤Şş¤¸ŻŔ§QĄÎ  ¨Ó¤ŔĂţ. Y
(a, b)
¨Ó¤ŔĂţ. Y
(a, b)  S, §ÚĚĄO [a, b]
ŞíĄÜ¦b S ¤¤©Ň¦ł©M (a, b) ¦PĂţŞş¤¸ŻŔ©Ň¦¨Şş¶°¦X. ĄO
S, §ÚĚĄO [a, b]
ŞíĄÜ¦b S ¤¤©Ň¦ł©M (a, b) ¦PĂţŞş¤¸ŻŔ©Ň¦¨Şş¶°¦X. ĄO
 ŞíĄÜ±N S ¤ŔĂţĄH«á©Ň¦¨Şş·sŞş¶°¦X. ¤]´N¬O»ˇ
ŞíĄÜ±N S ¤ŔĂţĄH«á©Ň¦¨Şş·sŞş¶°¦X. ¤]´N¬O»ˇ
 ¤¤Şş¤¸ŻŔłŁ¬O [a, b] łoşŘ§Î¦ˇ, ¨ä¤¤ a, b
¤¤Şş¤¸ŻŔłŁ¬O [a, b] łoşŘ§Î¦ˇ, ¨ä¤¤ a, b  D ĄB b
D ĄB b 0, ¦ÓĄBY
(a, b)
0, ¦ÓĄBY
(a, b)  (c, d ), «h¦b
(c, d ), «h¦b
 ¤¤
[a, b] = [c, d].
¤¤
[a, b] = [c, d].
˛¦b§ÚĚn¦b
 ¤¤©w¸qĄ[Şk©MĽŞk. Y
[a, b]
¤¤©w¸qĄ[Şk©MĽŞk. Y
[a, b] 
 ĄB
[c, d]
ĄB
[c, d] 
 , §ÚĚ©w:
, §ÚĚ©w:
[a, b] + [c, d] = [a . d + c . b, b . d] ĄH¤Î [a, b] . [c, d] = [a . c, b . d].
¬°¤°»ňłoĽË©wĄ[Şk©MĽŞk¬Ű«H¤j®a«Ü§ÖŞş¬ÝĄXło¬O±q¦ł˛zĽĆ¤WŞşĄ[Şk©MĽŞklĄÍĄX¨Ó.
¤]¬Ű«H¤j®aŞľąD¤U¤@¨B´N¬OnŔËĹçłoĽË©wŞşĄ[Şk©MĽŞk¬O well-defined.
şĄýnŔˬdŞş¬OłoĽË©wŞş
[a, b] + [c, d] ©M
[a, b] . [c, d] ·|¸¨¦b
 ¤¤, ¤]´N¬O»ˇ
b . d
¤¤, ¤]´N¬O»ˇ
b . d 0. ĄŃ b
0. ĄŃ b 0 ĄB d
0 ĄB d 0 ĄH¤Î D ¬O integral domain, ·íµMĄi±o
b . d
0 ĄH¤Î D ¬O integral domain, ·íµMĄi±o
b . d 0.
±µ¤U¨ÓnŔˬdŞş¬OY
[a, b] = [a', b'] ĄB
[c, d] = [c', d'], «h
[a, b] + [c, d] = [a', b'] + [c', d'] ĄH¤Î
[a, b] . [c, d] = [a', b'] . [c', d']. ±q©w¸qŞľnŔËĹç
[a, b] + [c, d] = [a', b'] + [c', d'] µĄ©ónĹçĂŇ
0.
±µ¤U¨ÓnŔˬdŞş¬OY
[a, b] = [a', b'] ĄB
[c, d] = [c', d'], «h
[a, b] + [c, d] = [a', b'] + [c', d'] ĄH¤Î
[a, b] . [c, d] = [a', b'] . [c', d']. ±q©w¸qŞľnŔËĹç
[a, b] + [c, d] = [a', b'] + [c', d'] µĄ©ónĹçĂŇ
(a . d + c . b) . (b' . d') = (a' . d' + c' . b') . (b . d ).
µM¦Ó§QĄÎ
a . b' = a' . b ĄH¤Î
c . d' = c' . d ±o
| (a . d + c . b) . (b' . d') |
= |
(a . b') . (d . d') + (c . d') . (b' . b) |
|
| |
= |
(a' . b) . (d . d') + (c' . d ) . (b' . b) |
|
| |
= |
(a' . d' + c' . b') . (b . d ). |
|
¦P˛z, nŔˬd
[a, b] . [c, d] = [a', b'] . [c', d'] µĄ©ónĹçĂŇ
(a . c) . (b' . d') = (a' . c') . (b . d ). µM¦Ó§QĄÎ
a . b' = a' . b ĄH¤Î
c . d' = c' . d ±o
(a . c) . (b' . d') = (a . b') . (c . d') = (a' . b) . (c' . d )= (a' . c') . (b . d ).
¬JµM¦b
 ¤¤Ąi©w¸qĄ[Şk©MĽŞk, §Ú̦۵M·|°Ý
¤¤Ąi©w¸qĄ[Şk©MĽŞk, §Ú̦۵M·|°Ý
 ¬O§_¬O¤@Ó ring, ¤]´N¬OnŔˬd (R1)-(R8).
ło¤@łs¦ęŞşŔˬdÁöµM¤ŁĂř, ¦ý¬O«ÜÁc˝Ć§ÚĚ´N˛¤ąL. ¨Ćąę¤W
¬O§_¬O¤@Ó ring, ¤]´N¬OnŔˬd (R1)-(R8).
ło¤@łs¦ęŞşŔˬdÁöµM¤ŁĂř, ¦ý¬O«ÜÁc˝Ć§ÚĚ´N˛¤ąL. ¨Ćąę¤W
 ¬O¤@Ó commutative ring with 1. ¨ä¤¤
¬O¤@Ó commutative ring with 1. ¨ä¤¤
 Şş 0 ¬O
[0, 1] ¦Ó 1 ¬O [1, 1]. łoĄiĄHĄÎ
Şş 0 ¬O
[0, 1] ¦Ó 1 ¬O [1, 1]. łoĄiĄHĄÎ
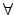 [a, b]
[a, b] 
 «h
[a, b] + [0, 1] = [a, b] ĄH¤Î
[a, b] . [1, 1] = [a, b] Ăұo. ¦Ü©ó
«h
[a, b] + [0, 1] = [a, b] ĄH¤Î
[a, b] . [1, 1] = [a, b] Ăұo. ¦Ü©ó
 ¬O commutative ĄiĄŃ D ¬O integral domain Şş°˛ł]Şľ
D ¬O commutative ¬G±o
[a, b] . [c, d] = [a . c, b . d] = [c, d] . [a, b].
¬O commutative ĄiĄŃ D ¬O integral domain Şş°˛ł]Şľ
D ¬O commutative ¬G±o
[a, b] . [c, d] = [a . c, b . d] = [c, d] . [a, b].
§Ú̳̲תşĄŘŞşnĂŇ©ú
 ¬O¤@Ó field, ¤]´N¬O»ˇąďĄô·NŞş
[a, b]
¬O¤@Ó field, ¤]´N¬O»ˇąďĄô·NŞş
[a, b] 
 ĄB
[a, b]
ĄB
[a, b] [0, 1] ĄiĄH§ä¨ě
[c, d]
[0, 1] ĄiĄH§ä¨ě
[c, d] 
 ¨Ď±o
[a, b] . [c, d] = [1, 1]. ¦]¬°
[a, b]
¨Ď±o
[a, b] . [c, d] = [1, 1]. ¦]¬°
[a, b] [0, 1]
¬GŞľ a
[0, 1]
¬GŞľ a 0, ©ŇĄH
[b, a]
0, ©ŇĄH
[b, a] 
 . «Ü®e©ö±oŞľ
[a, b] . [b, a] = [a . b, a . b] = [1, 1]. Á`¤§, Ąô·N
. «Ü®e©ö±oŞľ
[a, b] . [b, a] = [a . b, a . b] = [1, 1]. Á`¤§, Ąô·N
 ¤¤«D
0 Şş¤¸ŻŔłŁ¬O unit, ©ŇĄH
¤¤«D
0 Şş¤¸ŻŔłŁ¬O unit, ©ŇĄH
 ¬O¤@Ó field, §Ú̺٤§¬°
D Şş quotient field ©Î fraction field.
¬O¤@Ó field, §Ú̺٤§¬°
D Şş quotient field ©Î fraction field.
D Şş quotient field
 ¦ł¤@Ó«nŞş©Ę˝č, ´N¬OĄ¦¬OĄ]§t
D łĚ¤pŞş field. ło¸Ě¦łĄó¨Ć±ˇ§Ú̱o»ˇ©ú¤@¤U.
§ÚĚ´ŁąL¦bĄNĽĆ¤¤łq±`±N¨âÓ isomorphic ŞşŞF¦č¬Ý¦¨¬O¤@ĽËŞş. ¨Ćąę¤W
¦ł¤@Ó«nŞş©Ę˝č, ´N¬OĄ¦¬OĄ]§t
D łĚ¤pŞş field. ło¸Ě¦łĄó¨Ć±ˇ§Ú̱o»ˇ©ú¤@¤U.
§ÚĚ´ŁąL¦bĄNĽĆ¤¤łq±`±N¨âÓ isomorphic ŞşŞF¦č¬Ý¦¨¬O¤@ĽËŞş. ¨Ćąę¤W
 ¨Ă¨S¦łŻuĄżŞşĄ]§t D, ÄY®ć¨Ó»ˇŔł¸Ó¬O
¨Ă¨S¦łŻuĄżŞşĄ]§t D, ÄY®ć¨Ó»ˇŔł¸Ó¬O
 ¤¤¦ł¤@Ó subring ©M D ¬O isomorphic. ©ŇĄHło¸Ě©Ňż×
¤¤¦ł¤@Ó subring ©M D ¬O isomorphic. ©ŇĄHło¸Ě©Ňż×
 ¬OĄ]§t D łĚ¤pŞş field ŞíĄÜY F ¬O¤@Ó field ĄB¦ł¤@Ó subring ©M
D isomorphic, «h F ¤¤¦ł¤@Ó subring ©M
¬OĄ]§t D łĚ¤pŞş field ŞíĄÜY F ¬O¤@Ó field ĄB¦ł¤@Ó subring ©M
D isomorphic, «h F ¤¤¦ł¤@Ó subring ©M
 isomorphic.
isomorphic.
şĄý§ÚĚ´N¨Ó¬Ý D Ą]§t©óĄ¦Şş quotient field.
Proposition 7.4.1
°˛ł]
D ¬O¤@Ó integral domain, ĄBĄO

¬O
D Şş
quotient field, «hĄi§ä¨ě¤@Ó±q
D ¨ě

Şş injective
(¤@ąď¤@) ring homomorphism .
µý ©ú.
¦ŇĽ

:
D

©w¸q¦¨ąďĄô·NŞş
a  D
D,

(
a) = [
a, 1]. ĄŃ©óY
a,
b  D
D «h

(
a +
b) = [
a +
b, 1] = [
a, 1] + [
b, 1] =

(
a) +

(
b)
ĄB

(
a . b) = [
a . b, 1] = [
a, 1]
. [
b, 1] =

(
a)
. 
(
b).
¬GŞľ

¬O¤@Ó±q
D ¨ě

Şş ring homomorphism. ¦Ü©ónĂŇ

¬O¤@ąď¤@, §ÚĚĄunŔˬd
ker(

) = {0}. ĄŃ©ó

(0) = [0, 1] ¬GŞľ
0

ker(

). ˛Y
a 
ker(

), ŞíĄÜ

(
a) = [
a, 1] = [0, 1]. §QĄÎ©w¸q,
[
a, 1] = [0, 1] ŞíĄÜ
a . 1 = 0
. 1, ¬G±o
a = 0. ¦]¦ą±oĂŇ
ker(

) = {0}.

¦^ĹU Theorem 6.4.2 §i¶D§ÚĚ
D/ker( )
)  im(
im( )
¦Ó Proposition 7.4.1 §i¶D§ÚĚ
ker(
)
¦Ó Proposition 7.4.1 §i¶D§ÚĚ
ker( ) = {0} ¦]¦ą±o
D
) = {0} ¦]¦ą±o
D  im(
im( ). ¦ý¬O
im(
). ¦ý¬O
im( ) ¬O
) ¬O
 Şş
subring (Lemma 6.3.3), ¬GŞľ D ©M D Şş quotient field
Şş
subring (Lemma 6.3.3), ¬GŞľ D ©M D Şş quotient field
 ¤¤Şş¤@Ó subring ¬O isomorphic. ±µ¤U¨Ó§ÚĚnĂŇ©ú D
Şş quotient field ¬O¦łłoÓŻS©Ę¤§łĚ¤pŞş field.
¤¤Şş¤@Ó subring ¬O isomorphic. ±µ¤U¨Ó§ÚĚnĂŇ©ú D
Şş quotient field ¬O¦łłoÓŻS©Ę¤§łĚ¤pŞş field.
Proposition 7.4.2
°˛ł]
D ¬O¤@Ó integral domain, ĄBĄO

¬O
D Şş
quotient field. Y
F ¬O¤@Ó field ¨ä¤¤Ą]§t¤@Ó subring ©M
D
isomorphic, «h
F ¤¤¤]¦ł¤@Ó subring ©M

isomorphic.
µý ©ú.
ĄŃ°˛ł]Şľ¦s¦b¤@Ó¤@ąď¤@Şş ring homomorphism

:
D F
F.
§ÚĚ·Q§QĄÎłoÓ

»słyĄXĄt¤@Ó¤@ąď¤@Şş ring homomorphism

:

 F
F.
ąďĄô·NŞş
[a, b] 
 , §ÚĚ©w
, §ÚĚ©w
 ([a, b]) =
([a, b]) =  (a) .
(a) .  (b)-1. ·íµMło¸Ě§ÚĚnŔˬd
(b)-1. ·íµMło¸Ě§ÚĚnŔˬd  ¬O§_ well-defined.
¬O§_ well-defined.
şĄý§ÚĚŔˬd
 ([a, b]) ¬O§_¬O F ¤¤Şş¤¸ŻŔ. ĄŃ©ó
[a, b]
([a, b]) ¬O§_¬O F ¤¤Şş¤¸ŻŔ. ĄŃ©ó
[a, b] 
 , Şľ b
, Şľ b 0, ¦]¦ąĄŃ
0, ¦]¦ąĄŃ  ¬O¤@ąď¤@Şľ
¬O¤@ąď¤@Şľ
 (b) ¬O F ¤¤Şş¤@Ó¤ŁµĄ©ó 0 Şş¤¸ŻŔ. ©ŇĄHĄŃ F ¬O field
Şş°˛ł]Şľ
(b) ¬O F ¤¤Şş¤@Ó¤ŁµĄ©ó 0 Şş¤¸ŻŔ. ©ŇĄHĄŃ F ¬O field
Şş°˛ł]Şľ
 (b)-1
(b)-1  F. ¬G±oĂŇ
F. ¬G±oĂŇ
 ([a, b]) =
([a, b]) =  (a) .
(a) .  (b)-1
(b)-1  F. ±µµŰnŔˬd¬O§_Y
[a, b] = [c, d] «h
F. ±µµŰnŔˬd¬O§_Y
[a, b] = [c, d] «h
 ([a, b]) =
([a, b]) =  ([c, d]). (¦A¦¸´Łżô:
·í§ÚĚ«Řşc¤@Ó¨çĽĆ®É¦pŞG©w¸q°ě¸ĚŞş¤¸ŻŔŞşŞíĄÜŞk¤Ł°ß¤@,
§Ṳ́@©wnŔˬd¬O§_¦P¤@¤¸ŻŔ¨ä¤Ł¦PŞşŞíĄÜŞk·|łQ¬M®g¨ě¬Ű¦PŞşČ,
ĄH§KµoĄÍ¤@ąď¦hŞş±ˇŞp.) ¤]´N¬O»ˇY
a . d = c . b, nŔˬd¬O§_
([c, d]). (¦A¦¸´Łżô:
·í§ÚĚ«Řşc¤@Ó¨çĽĆ®É¦pŞG©w¸q°ě¸ĚŞş¤¸ŻŔŞşŞíĄÜŞk¤Ł°ß¤@,
§Ṳ́@©wnŔˬd¬O§_¦P¤@¤¸ŻŔ¨ä¤Ł¦PŞşŞíĄÜŞk·|łQ¬M®g¨ě¬Ű¦PŞşČ,
ĄH§KµoĄÍ¤@ąď¦hŞş±ˇŞp.) ¤]´N¬O»ˇY
a . d = c . b, nŔˬd¬O§_

(
a)
. 
(
b)
-1 =

(
c)
. 
(
d )
-1.
µM¦Ó§QĄÎ

¬O ring homomorphism Şľ

(
a . d )=

(
a)
. 
(
d )
ĄB

(
c . b) =

(
c)
. 
(
b). ¬GĄŃ
a . d =
c . b
Ąi±o

(
a . d )=

(
c . b) ¤]´N¬O»ˇ

(
a)
. 
(
d )=

(
c)
. 
(
b). ¤W¦ˇ¨âĂä¦UĽ¤W

(
d )
-1 . 
(
b)
-1 (§O§Ń¤F

(
b) ©M

(
d )
¬Ň¤ŁµĄ©ó 0) Ąi±o

(
a)
. 
(
b)
-1 =

(
c)
. 
(
d )
-1. ¦]¦ą

¬O¤@Ó well-defined Şş¨çĽĆ.
±µ¤U¨Ó§ÚĚĂŇ  ¬O¤@Ó ring homomorphism. ąďĄô·NŞş
[a, b],[c, d]
¬O¤@Ó ring homomorphism. ąďĄô·NŞş
[a, b],[c, d] 
 , ¨Ě
, ¨Ě  Şş©w¸q§Ú̦ł
Şş©w¸q§Ú̦ł

([
a,
b] + [
c,
d]) =

([
a . d +
c . b,
b . d]) =

(
a . d +
c . b)
. 
(
b . d )
-1
ĄB

([
a,
b]) +

([
c,
d]) =

(
a)
. 
(
b)
-1 +

(
c)
. 
(
d )
-1.
µM¦Ó§QĄÎ

¬O ring homomorphism, Ľ¤W

(
b . d )=

(
b)
. 
(
d ) §ÚĚ«Ü®e©öŔËĹç

(
a . d +
c . b)
. 
(
b . d )
-1 =

(
a)
. 
(
b)
-1 +

(
c)
. 
(
d )
-1.
¬GŞľ

([
a,
b] + [
c,
d]) =

([
a,
b]) +

([
c,
d]).
¦P˛zĄiĂŇ

([
a,
b]
. [
c,
d]) =

([
a . c,
b . d]) =

(
a . c)
. 
(
b . d )
-1 =

([
a,
b])
. 
([
c,
d]),
¬GŞľ

¬O¤@Ó
ring homomorphism.
łĚ«á§ÚĚĹçĂŇ  ¬O¤@ąď¤@Şş, ¤]´N¬OĹçĂŇ
ker(
¬O¤@ąď¤@Şş, ¤]´N¬OĹçĂŇ
ker( ) = {[0, 1]}.
°˛ł]
[a, b]
) = {[0, 1]}.
°˛ł]
[a, b]  ker(
ker( ), §Y
), §Y
 ([a, b]) =
([a, b]) =  (a) .
(a) .  (b)-1 = 0. Ľ¤W
(b)-1 = 0. Ľ¤W  (b) °¨¤WĄi±o
(b) °¨¤WĄi±o
 (a) = 0. ¦ýĄŃ©ó
(a) = 0. ¦ýĄŃ©ó  ¬O¤@ąď¤@, ¬GĄŃ
a
¬O¤@ąď¤@, ¬GĄŃ
a  ker(
ker( ) = {0}, ±o a = 0. ´«Ąy¸Ü»ˇ
[a, b] = [0, 1]. ©ŇĄH±oĂŇ
) = {0}, ±o a = 0. ´«Ąy¸Ü»ˇ
[a, b] = [0, 1]. ©ŇĄH±oĂŇ
 ¬O¤@ąď¤@.
¬O¤@ąď¤@.

±q¤µĄH«á, Y
 ¬° D Şş quotient field,
§Ú̱NŞ˝±µ¬Ý¦¨ D Ą]§t©ó
¬° D Şş quotient field,
§Ú̱NŞ˝±µ¬Ý¦¨ D Ą]§t©ó
 , ¤]´N¬O±N [a, 1] Ľg¦¨
a. ĄtĄ §Ú̱N
[a, b]
, ¤]´N¬O±N [a, 1] Ľg¦¨
a. ĄtĄ §Ú̱N
[a, b] 
 Ş˝±µĽg¦¨ a/b.
Ş˝±µĽg¦¨ a/b.



¤U¤@¶: Integral Domain ¤WŞş¤Ŕ¸Ń©Ę˝č
¤W¤@¶: ¤@¨Ç±`¨ŁŞş Rings
«e¤@¶: Polynomials over the Integers
Administrator
2005-06-18
![]() D, b
D, b![]() 0}. şĄý§Ú̱N¦b S ¤¤©w¤@Ó equivalence relation. ąď©ó S
¤¤Şş¨â¤¸ŻŔ
(a, b),(c, d )
0}. şĄý§Ú̱N¦b S ¤¤©w¤@Ó equivalence relation. ąď©ó S
¤¤Şş¨â¤¸ŻŔ
(a, b),(c, d ) ![]() S, §ÚĚĄO
S, §ÚĚĄO
![]() ło¤@Ó relation ¬O¤@Ó equivalence relation:
ło¤@Ó relation ¬O¤@Ó equivalence relation:
![]() ¬O S ¤¤Şş¤@Ó equivalence relation, §ÚĚ´NĄiĄH±N
S ¤¤Şş¤¸ŻŔ§QĄÎ
¬O S ¤¤Şş¤@Ó equivalence relation, §ÚĚ´NĄiĄH±N
S ¤¤Şş¤¸ŻŔ§QĄÎ ![]() ¨Ó¤ŔĂţ. Y
(a, b)
¨Ó¤ŔĂţ. Y
(a, b) ![]() S, §ÚĚĄO [a, b]
ŞíĄÜ¦b S ¤¤©Ň¦ł©M (a, b) ¦PĂţŞş¤¸ŻŔ©Ň¦¨Şş¶°¦X. ĄO
S, §ÚĚĄO [a, b]
ŞíĄÜ¦b S ¤¤©Ň¦ł©M (a, b) ¦PĂţŞş¤¸ŻŔ©Ň¦¨Şş¶°¦X. ĄO
![]() ŞíĄÜ±N S ¤ŔĂţĄH«á©Ň¦¨Şş·sŞş¶°¦X. ¤]´N¬O»ˇ
ŞíĄÜ±N S ¤ŔĂţĄH«á©Ň¦¨Şş·sŞş¶°¦X. ¤]´N¬O»ˇ
![]() ¤¤Şş¤¸ŻŔłŁ¬O [a, b] łoşŘ§Î¦ˇ, ¨ä¤¤ a, b
¤¤Şş¤¸ŻŔłŁ¬O [a, b] łoşŘ§Î¦ˇ, ¨ä¤¤ a, b ![]() D ĄB b
D ĄB b![]() 0, ¦ÓĄBY
(a, b)
0, ¦ÓĄBY
(a, b) ![]() (c, d ), «h¦b
(c, d ), «h¦b
![]() ¤¤
[a, b] = [c, d].
¤¤
[a, b] = [c, d].
![]() ¤¤©w¸qĄ[Şk©MĽŞk. Y
[a, b]
¤¤©w¸qĄ[Şk©MĽŞk. Y
[a, b] ![]()
![]() ĄB
[c, d]
ĄB
[c, d] ![]()
![]() , §ÚĚ©w:
, §ÚĚ©w:
![]() ¤¤Ąi©w¸qĄ[Şk©MĽŞk, §Ú̦۵M·|°Ý
¤¤Ąi©w¸qĄ[Şk©MĽŞk, §Ú̦۵M·|°Ý
![]() ¬O§_¬O¤@Ó ring, ¤]´N¬OnŔˬd (R1)-(R8).
ło¤@łs¦ęŞşŔˬdÁöµM¤ŁĂř, ¦ý¬O«ÜÁc˝Ć§ÚĚ´N˛¤ąL. ¨Ćąę¤W
¬O§_¬O¤@Ó ring, ¤]´N¬OnŔˬd (R1)-(R8).
ło¤@łs¦ęŞşŔˬdÁöµM¤ŁĂř, ¦ý¬O«ÜÁc˝Ć§ÚĚ´N˛¤ąL. ¨Ćąę¤W
![]() ¬O¤@Ó commutative ring with 1. ¨ä¤¤
¬O¤@Ó commutative ring with 1. ¨ä¤¤
![]() Şş 0 ¬O
[0, 1] ¦Ó 1 ¬O [1, 1]. łoĄiĄHĄÎ
Şş 0 ¬O
[0, 1] ¦Ó 1 ¬O [1, 1]. łoĄiĄHĄÎ
![]() [a, b]
[a, b] ![]()
![]() «h
[a, b] + [0, 1] = [a, b] ĄH¤Î
[a, b] . [1, 1] = [a, b] Ăұo. ¦Ü©ó
«h
[a, b] + [0, 1] = [a, b] ĄH¤Î
[a, b] . [1, 1] = [a, b] Ăұo. ¦Ü©ó
![]() ¬O commutative ĄiĄŃ D ¬O integral domain Şş°˛ł]Şľ
D ¬O commutative ¬G±o
[a, b] . [c, d] = [a . c, b . d] = [c, d] . [a, b].
¬O commutative ĄiĄŃ D ¬O integral domain Şş°˛ł]Şľ
D ¬O commutative ¬G±o
[a, b] . [c, d] = [a . c, b . d] = [c, d] . [a, b].
![]() ¬O¤@Ó field, ¤]´N¬O»ˇąďĄô·NŞş
[a, b]
¬O¤@Ó field, ¤]´N¬O»ˇąďĄô·NŞş
[a, b] ![]()
![]() ĄB
[a, b]
ĄB
[a, b]![]() [0, 1] ĄiĄH§ä¨ě
[c, d]
[0, 1] ĄiĄH§ä¨ě
[c, d] ![]()
![]() ¨Ď±o
[a, b] . [c, d] = [1, 1]. ¦]¬°
[a, b]
¨Ď±o
[a, b] . [c, d] = [1, 1]. ¦]¬°
[a, b]![]() [0, 1]
¬GŞľ a
[0, 1]
¬GŞľ a![]() 0, ©ŇĄH
[b, a]
0, ©ŇĄH
[b, a] ![]()
![]() . «Ü®e©ö±oŞľ
[a, b] . [b, a] = [a . b, a . b] = [1, 1]. Á`¤§, Ąô·N
. «Ü®e©ö±oŞľ
[a, b] . [b, a] = [a . b, a . b] = [1, 1]. Á`¤§, Ąô·N
![]() ¤¤«D
0 Şş¤¸ŻŔłŁ¬O unit, ©ŇĄH
¤¤«D
0 Şş¤¸ŻŔłŁ¬O unit, ©ŇĄH
![]() ¬O¤@Ó field, §Ú̺٤§¬°
D Şş quotient field ©Î fraction field.
¬O¤@Ó field, §Ú̺٤§¬°
D Şş quotient field ©Î fraction field.
![]() ¦ł¤@Ó«nŞş©Ę˝č, ´N¬OĄ¦¬OĄ]§t
D łĚ¤pŞş field. ło¸Ě¦łĄó¨Ć±ˇ§Ú̱o»ˇ©ú¤@¤U.
§ÚĚ´ŁąL¦bĄNĽĆ¤¤łq±`±N¨âÓ isomorphic ŞşŞF¦č¬Ý¦¨¬O¤@ĽËŞş. ¨Ćąę¤W
¦ł¤@Ó«nŞş©Ę˝č, ´N¬OĄ¦¬OĄ]§t
D łĚ¤pŞş field. ło¸Ě¦łĄó¨Ć±ˇ§Ú̱o»ˇ©ú¤@¤U.
§ÚĚ´ŁąL¦bĄNĽĆ¤¤łq±`±N¨âÓ isomorphic ŞşŞF¦č¬Ý¦¨¬O¤@ĽËŞş. ¨Ćąę¤W
![]() ¨Ă¨S¦łŻuĄżŞşĄ]§t D, ÄY®ć¨Ó»ˇŔł¸Ó¬O
¨Ă¨S¦łŻuĄżŞşĄ]§t D, ÄY®ć¨Ó»ˇŔł¸Ó¬O
![]() ¤¤¦ł¤@Ó subring ©M D ¬O isomorphic. ©ŇĄHło¸Ě©Ňż×
¤¤¦ł¤@Ó subring ©M D ¬O isomorphic. ©ŇĄHło¸Ě©Ňż×
![]() ¬OĄ]§t D łĚ¤pŞş field ŞíĄÜY F ¬O¤@Ó field ĄB¦ł¤@Ó subring ©M
D isomorphic, «h F ¤¤¦ł¤@Ó subring ©M
¬OĄ]§t D łĚ¤pŞş field ŞíĄÜY F ¬O¤@Ó field ĄB¦ł¤@Ó subring ©M
D isomorphic, «h F ¤¤¦ł¤@Ó subring ©M
![]() isomorphic.
isomorphic.
![]() )
) ![]() im(
im(![]() )
¦Ó Proposition 7.4.1 §i¶D§ÚĚ
ker(
)
¦Ó Proposition 7.4.1 §i¶D§ÚĚ
ker(![]() ) = {0} ¦]¦ą±o
D
) = {0} ¦]¦ą±o
D ![]() im(
im(![]() ). ¦ý¬O
im(
). ¦ý¬O
im(![]() ) ¬O
) ¬O
![]() Şş
subring (Lemma 6.3.3), ¬GŞľ D ©M D Şş quotient field
Şş
subring (Lemma 6.3.3), ¬GŞľ D ©M D Şş quotient field
![]() ¤¤Şş¤@Ó subring ¬O isomorphic. ±µ¤U¨Ó§ÚĚnĂŇ©ú D
Şş quotient field ¬O¦łłoÓŻS©Ę¤§łĚ¤pŞş field.
¤¤Şş¤@Ó subring ¬O isomorphic. ±µ¤U¨Ó§ÚĚnĂŇ©ú D
Şş quotient field ¬O¦łłoÓŻS©Ę¤§łĚ¤pŞş field.
![]()
![]() , §ÚĚ©w
, §ÚĚ©w
![]() ([a, b]) =
([a, b]) = ![]() (a) .
(a) . ![]() (b)-1. ·íµMło¸Ě§ÚĚnŔˬd
(b)-1. ·íµMło¸Ě§ÚĚnŔˬd ![]() ¬O§_ well-defined.
¬O§_ well-defined.
![]() ([a, b]) ¬O§_¬O F ¤¤Şş¤¸ŻŔ. ĄŃ©ó
[a, b]
([a, b]) ¬O§_¬O F ¤¤Şş¤¸ŻŔ. ĄŃ©ó
[a, b] ![]()
![]() , Şľ b
, Şľ b![]() 0, ¦]¦ąĄŃ
0, ¦]¦ąĄŃ ![]() ¬O¤@ąď¤@Şľ
¬O¤@ąď¤@Şľ
![]() (b) ¬O F ¤¤Şş¤@Ó¤ŁµĄ©ó 0 Şş¤¸ŻŔ. ©ŇĄHĄŃ F ¬O field
Şş°˛ł]Şľ
(b) ¬O F ¤¤Şş¤@Ó¤ŁµĄ©ó 0 Şş¤¸ŻŔ. ©ŇĄHĄŃ F ¬O field
Şş°˛ł]Şľ
![]() (b)-1
(b)-1 ![]() F. ¬G±oĂŇ
F. ¬G±oĂŇ
![]() ([a, b]) =
([a, b]) = ![]() (a) .
(a) . ![]() (b)-1
(b)-1 ![]() F. ±µµŰnŔˬd¬O§_Y
[a, b] = [c, d] «h
F. ±µµŰnŔˬd¬O§_Y
[a, b] = [c, d] «h
![]() ([a, b]) =
([a, b]) = ![]() ([c, d]). (¦A¦¸´Łżô:
·í§ÚĚ«Řşc¤@Ó¨çĽĆ®É¦pŞG©w¸q°ě¸ĚŞş¤¸ŻŔŞşŞíĄÜŞk¤Ł°ß¤@,
§Ṳ́@©wnŔˬd¬O§_¦P¤@¤¸ŻŔ¨ä¤Ł¦PŞşŞíĄÜŞk·|łQ¬M®g¨ě¬Ű¦PŞşČ,
ĄH§KµoĄÍ¤@ąď¦hŞş±ˇŞp.) ¤]´N¬O»ˇY
a . d = c . b, nŔˬd¬O§_
([c, d]). (¦A¦¸´Łżô:
·í§ÚĚ«Řşc¤@Ó¨çĽĆ®É¦pŞG©w¸q°ě¸ĚŞş¤¸ŻŔŞşŞíĄÜŞk¤Ł°ß¤@,
§Ṳ́@©wnŔˬd¬O§_¦P¤@¤¸ŻŔ¨ä¤Ł¦PŞşŞíĄÜŞk·|łQ¬M®g¨ě¬Ű¦PŞşČ,
ĄH§KµoĄÍ¤@ąď¦hŞş±ˇŞp.) ¤]´N¬O»ˇY
a . d = c . b, nŔˬd¬O§_
![]() ¬O¤@Ó ring homomorphism. ąďĄô·NŞş
[a, b],[c, d]
¬O¤@Ó ring homomorphism. ąďĄô·NŞş
[a, b],[c, d] ![]()
![]() , ¨Ě
, ¨Ě ![]() Şş©w¸q§Ú̦ł
Şş©w¸q§Ú̦ł
![]() ¬O¤@ąď¤@Şş, ¤]´N¬OĹçĂŇ
ker(
¬O¤@ąď¤@Şş, ¤]´N¬OĹçĂŇ
ker(![]() ) = {[0, 1]}.
°˛ł]
[a, b]
) = {[0, 1]}.
°˛ł]
[a, b] ![]() ker(
ker(![]() ), §Y
), §Y
![]() ([a, b]) =
([a, b]) = ![]() (a) .
(a) . ![]() (b)-1 = 0. Ľ¤W
(b)-1 = 0. Ľ¤W ![]() (b) °¨¤WĄi±o
(b) °¨¤WĄi±o
![]() (a) = 0. ¦ýĄŃ©ó
(a) = 0. ¦ýĄŃ©ó ![]() ¬O¤@ąď¤@, ¬GĄŃ
a
¬O¤@ąď¤@, ¬GĄŃ
a ![]() ker(
ker(![]() ) = {0}, ±o a = 0. ´«Ąy¸Ü»ˇ
[a, b] = [0, 1]. ©ŇĄH±oĂŇ
) = {0}, ±o a = 0. ´«Ąy¸Ü»ˇ
[a, b] = [0, 1]. ©ŇĄH±oĂŇ
![]() ¬O¤@ąď¤@.
¬O¤@ąď¤@.
![]()
![]() ¬° D Şş quotient field,
§Ú̱NŞ˝±µ¬Ý¦¨ D Ą]§t©ó
¬° D Şş quotient field,
§Ú̱NŞ˝±µ¬Ý¦¨ D Ą]§t©ó
![]() , ¤]´N¬O±N [a, 1] Ľg¦¨
a. ĄtĄ §Ú̱N
[a, b]
, ¤]´N¬O±N [a, 1] Ľg¦¨
a. ĄtĄ §Ú̱N
[a, b] ![]()
![]() Ş˝±µĽg¦¨ a/b.
Ş˝±µĽg¦¨ a/b.