


§U§@≠∂: ØSÆÌ™∫ Ideals
§W§@≠∂: §§Ø≈ Ring ™∫© ΩË
´e§@≠∂: Ring Homomorphism
©M group §@ºÀ, ring §]¶≥§T≠” isomorphism ©w≤z. •—©Ûß⁄≠ö≥≤¶®™∫
group isomorphism ©w≤z•i•Œ, ≥o§T≠” isomorphism ©w≤z¥X•G•i•H™Ω±µ±¿±o,
ß⁄≠Õu≠n≈Á√“≠º™k≥°§¿ßY•i.
Definition 6.4.1
¶p™G®‚≠” rings
R ©M
R'
∂°ßA•i•H߉®Ï§@≠” ring homomorphism ¨O isomorphism (ßY 1-1 •B onto),
´hß⁄≠Ã∫Ÿ
R ©M
R' ≥o®‚≠” ring ¨O
isomorphic, ∞O¨∞:
R  R'
R'.
Theorem 6.4.2 (First Isomorphism Theorem)
≠Y

:
R R'
R' ¨O§@≠” ring homomorphism, ´h
µ˝ ©˙.
≠∫•˝™`∑N•— Lemma
6.3.3 ™æ
im(

) ¨O§@≠” ring •B
ker(

) ¨O
R ™∫ ideal, ©“•H
R/ker(

) §]¨O§@≠” ring. ßQ•Œ©M≤ƒ§@≠” group isomorphism
©w≤z¨€¶P™∫§Ë™k, ß⁄≠öb
R/ker(

) ≥o§@≠” quotient ring ©M
im(

) ≥o≠” ring §ß∂°ß‰®Ï§@≠”®Áº∆. ¶Aª°©˙≥o≠”®Áº∆¨O ring
homomorphism, ≥ô·¶A≈Á√“•¶¨O 1-1 •B onto.
ß⁄≠Õi•HßQ•Œ  ªs≥y•H§U™∫®Áº∆:
ªs≥y•H§U™∫®Áº∆:

:
R/ker(

)
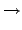
im(

);
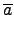
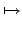

(
a),
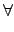
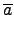
 R
R/ker(

).
ß⁄≠Ã≠∫•˝ª°©˙

¨O§@≠”`¶n®Áº∆' (well defined
function): ¶p™G
a,
b  R
R ®œ±o

©M
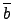
¶b
R/ker(

) §§¨O¨€¶P™∫. ß⁄≠Õ≤∂∑ª°©˙

(
a) =

(
b). ¡ˆµM
a b
b, §£πL•—

=
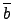
™æ
a ©M
b ¶b•H
ker(

) ≥o≠” ideal ™∫§¿√˛§U¨O¶P√˛™∫. ßOß—§F
a ©M
b ¶P√˛™Ì•Ð
a -
b 
ker(

). §]¥N¨Oª°

(
a -
b) = 0. ¶AßQ•Œ

¨O ring
homomorphism ™∫∞≤≥], ß⁄≠ño

(
a) -

(
b) =

(
a -
b) = 0. ßY

(
a) =

(
b). ©“•Hß⁄≠ês≥y™∫

¨O§@≠” well defined
function.
±µ§U®”√“  ¨O§@≠” ring homomorphism: πÔ•Ù∑N™∫
¨O§@≠” ring homomorphism: πÔ•Ù∑N™∫
 ,
,
 R/ker(
R/ker( ), ß⁄≠ö≥
), ß⁄≠ö≥

(
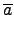
+
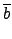
) =

(
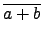
) =

(
a +
b) •B

(
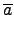 .
. 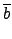
) =

(
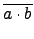
) =

(
a . b).
•t§@§Ë≠±¶]¨∞

¨O ring homomorphism, ©“•H

(
a +
b) =

(
a) +

(
b) =

(
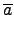
) +

(
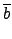
) •B

(
a . b) =

(
a)
. 
(
b) =

(
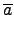
)
. 
(
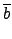
).
µ≤¶X•H§W§G¶°, ß⁄≠Õi±o

(
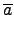
+
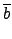
) =

(
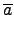
) +

(
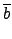
) •B

(
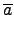 .
. 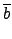
) =

(
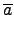
)
. 
(
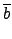
).
ß⁄≠Ã≥ô·≠n√“©˙  ¨O 1-1 •B onto.
≥o®‰πͧ£•≤√“§F(∑̵MßA≠n¶h¶π§@¡|§]®S√ˆ´Y), ¶]¨∞ß⁄≠öb Theorem
2.6.1 §w√“πL
¨O 1-1 •B onto.
≥o®‰πͧ£•≤√“§F(∑̵MßA≠n¶h¶π§@¡|§]®S√ˆ´Y), ¶]¨∞ß⁄≠öb Theorem
2.6.1 §w√“πL  ≥o≠”®Áº∆¶b•[™k¨ð¶®¨O group homomorphism
§w∏g¨O 1-1 •B onto.
≥o≠”®Áº∆¶b•[™k¨ð¶®¨O group homomorphism
§w∏g¨O 1-1 •B onto.
¡`µ≤: ß⁄≠Ã√“±o§F  ¨O§@≠”±q
G/ker(
¨O§@≠”±q
G/ker( ) ®Ï
im(
) ®Ï
im( ) ™∫
isomorphism. ©“•H
G/ker(
) ™∫
isomorphism. ©“•H
G/ker( )
)  im(
im( ).
).

∑̵M§F¶p™G©w≤z§§™∫  ¨O onto. ®∫ªÚß⁄≠Ùæ
im(
¨O onto. ®∫ªÚß⁄≠Ùæ
im( ) = R'.
¶]¶πß⁄≠ö≥•H§U™∫§Þ≤z:
) = R'.
¶]¶πß⁄≠ö≥•H§U™∫§Þ≤z:
≤¶bß⁄≠ð¨ð ring ™∫≤ƒ§G≠” isomorphism ©w≤z. •¶¿≥∏”¨O´ÁºÀ™∫ߌ¶°©O?
ß⁄≠Õ˝¶^≈U§@§U group ™∫±°™p: µπ©w§@ group G, ≠Y H ¨O G ™∫
subgroup •B N ¨O G ™∫ normal subgroup. ´h H  N ¨O H ™∫
normal subgroup, •B
H/(H
N ¨O H ™∫
normal subgroup, •B
H/(H  N)
N)  (H . N)/N. ¶n≤¶bß⁄≠Ãß‚
group ¥´¶® ring, subgroup ¥´¶® subring, normal subgroup ¥´¶® ideal,
≥ô·ßOß—§F±N≠ºßÔ¨∞•[.
(H . N)/N. ¶n≤¶bß⁄≠Ãß‚
group ¥´¶® ring, subgroup ¥´¶® subring, normal subgroup ¥´¶® ideal,
≥ô·ßOß—§F±N≠ºßÔ¨∞•[.
Theorem 6.4.4 (Second Isomorphism Theorem)
≠Y
R ¨O§@≠” ring,
S ¨O
R ™∫ subring •B
I ¨O
R ™∫ ideal, ´h
S  I
I ¨O
S ™∫ ideal, •B
S/(
S 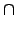 I
I)
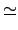
(
S +
I)/
I.
µ˝ ©˙.
≠∫•˝™`∑N™∫¨O•— Lemma
6.2.1 ™æ
S +
I ¨O
R ™∫ subring, •B
I  S
S +
I ¶]¶π™æ
I ¨O
S +
I ™∫ ideal (Ω–∞—¶“
6.2
∏`™∫≥ô·). ©“•H (
S +
I)/
I ΩTπͨO§@≠” ring.
¶p¶P¶b group ™∫±°™p, ß⁄≠Ã∑Q•Œ first isomorphism ©w≤z®”√“©˙¶π©w≤z.
ß⁄≠Õ˝ß‰§@≠”±q S ®Ï (S + I)/I ™∫®Áº∆. ¶“º
 : S
: S (S + I)/I,
®‰§§πÔ©“¶≥™∫ s
(S + I)/I,
®‰§§πÔ©“¶≥™∫ s  S ß⁄≠ö≥
S ß⁄≠ö≥
 (s) =
(s) = 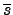 .
.
≤¶b≠n√“  ¨O§@≠” ring homomorphism. ®∆πͧWπÔ•Ù∑N™∫ s, s'
¨O§@≠” ring homomorphism. ®∆πͧWπÔ•Ù∑N™∫ s, s'  S, ß⁄≠ö≥
S, ß⁄≠ö≥

(
s +
s') =
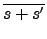
=
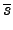
+
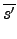
=

(
s) +

(
s') •B

(
s . s') =
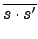
=
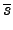 .
. 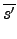
=

(
s)
. 
(
s').
ßQ•Œ Theorem 2.6.4 ™∫√“©˙, ß⁄≠ño
 : S
: S (S + I)/I ¨O onto.
¶]¶π•i•H•Œ First Isomorphism Theorem (Corollary 6.4.3) ±o®Ï
(S + I)/I ¨O onto.
¶]¶π•i•H•Œ First Isomorphism Theorem (Corollary 6.4.3) ±o®Ï
S/ker(

)
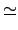
(
S +
I)/
I.
¨∆ªÚ¨O
ker(

) ©O? ®Ã©w∏q
ker(

) ¨O
S §§™∫§∏Ø¿
s ®œ±o

(
s) ¨O (
S +
I)/
I ™∫
identity,

. §]¥N¨Oª°

(
s) =
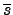
=

. ßOß—§F
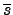
=

™Ì•Ð
s - 0 =
s  I
I. •—¶π™æ
ker(

)
™∫§∏Ø¿¨J≠n¶b
S §§§]≠n¶b
I §§; ¥´•y∏Ъ°
ker(

)
 S
S  I
I. §œ§ß≠Y
a  S
S  I
I, ´h¶]
a  I
I ±o

(
a) =

=

. ¨G
S  I
I 
ker(

). •—¶π™æ
ker(

) =
S  I
I. ¶]¶πß⁄≠Õ— Lemma
6.3.3 ™æ
S  I
I ¨O
S ™∫ ideal §]•— First Isomorphism
Theorem ™æ
S/(
S 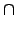 I
I)
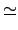
(
S +
I)/
I.

≥ô·ß⁄≠ð≤ƒ§T≠” isomorphism ©w≤z. ¶PºÀ™∫, ±N Theorem 2.6.5
§§™∫ group ¥´¶® ring §Œ normal subgroup ¥´¶® ideal, ß⁄≠ö≥•H§U§ß≤ƒ§T
isomorphism ©w≤z:
Theorem 6.4.5 (Third Isomorphism Theorem)
≠Y

:
R R'
R' ¨O§@≠” onto ™∫ ring homomorphism. ∞≤≥]
J' ¨O
R' ™∫§@≠” ideal. •O
´h
J ¨O
R ™∫ ideal •B
R/
J 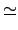 R'
R'/
J'.
µ˝ ©˙.
ß⁄≠éw

:
R R'
R'/
J', ∫°®¨

(
a) =
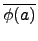
,
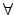 a
a  R
R.
•—  ¨O ring homomorphism ™æ
¨O ring homomorphism ™æ

(
a +
b) =
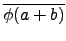
=
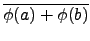
=
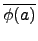
+
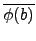
=

(
a) +

(
b)
•B

(
a . b) =
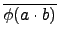
=
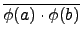
=
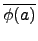 .
. 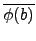
=

(
a)
. 
(
b).
¨G

¨O§@≠”±q
R ®Ï
R'/
J' ™∫ ring homomorphism.
¶p´e, ß⁄≠Õi•Œ Theorem 2.6.5 ™∫√“©˙™æ
 : R
: R R'/J' ¨O§@≠”
onto ™∫ ring homomorphism, ß⁄≠öA¶∏•Œ First Isomorphism Theorem ™æ
R'/J' ¨O§@≠”
onto ™∫ ring homomorphism, ß⁄≠öA¶∏•Œ First Isomorphism Theorem ™æ
R/ker(

)
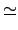 R'
R'/
J'.
¨∆ªÚ¨O
ker(

) ©O? ≠Y
a 
ker(

) ßY

(
a) =
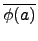
=

, §]¥N¨Oª°

(
a) ©M 0 ¶b•Œ
J' ™∫§¿√˛§U¨O¶P√˛™∫. ©“•H

(
a) - 0 =

(
a)
 J'
J'. •—
J ™∫©w∏q™æ, ≥o™Ì•Ð
a  J
J. ¨G
ker(

)
 J
J. •t• ≠Y
a  J
J, ´h

(
a)
 J'
J' ¨G¶b
R'/
J' §§

(
a) =
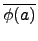
=

. ¶]¶π
a 
ker(

), ±o
J 
ker(

). §]¥N¨Oª°
ker(

) =
J
•B•— Lemma
6.3.3 ™æ
J ¨O
R ™∫ ideal (®‰πÍß⁄≠öb Theorem
6.3.5 §w™æ
J ¨O
R ™∫ ideal).

≥ô·ß⁄≠ÃßQ•Œ Correspondence Theorem ®”¨ð Third Isomorphism Theorem
™∫§@≠”ØSÆÌ™¨™p. •O I ¨O R ™∫ ideal,
 : R
: R R/I ¨O©w∏q¶®
R/I ¨O©w∏q¶®
 (a) =
(a) =  ≥o≠” onto ™∫ ring homomorphism. •Ù∑N R/I
§§™∫ ideal J' •—´e Corollary 6.3.7 ™æ¨O•— R §§™∫¨Y§@
ideal J ßQ•Œ
≥o≠” onto ™∫ ring homomorphism. •Ù∑N R/I
§§™∫ ideal J' •—´e Corollary 6.3.7 ™æ¨O•— R §§™∫¨Y§@
ideal J ßQ•Œ  ±o®Ï: §]¥N¨Oª°
J' =
±o®Ï: §]¥N¨Oª°
J' =  (J) = J/I. ¨G•— Theorem
6.4.5 ß⁄≠ö≥•H§U™∫©w≤z(¶≥™∫Æ—¨O∫Ÿ≥o≠”¨∞ Third Isomorphism
Theorem.)
(J) = J/I. ¨G•— Theorem
6.4.5 ß⁄≠ö≥•H§U™∫©w≤z(¶≥™∫Æ—¨O∫Ÿ≥o≠”¨∞ Third Isomorphism
Theorem.)
Theorem 6.4.6 (Third Isomorphism Theorem)
≠Y
R ¨O§@≠” ring,
I ¨O
R ™∫§@≠” ideal. ´h
R/
I §§™∫•Ù§@ ideal
≥£¨O
J/
I ≥o∫ÿߌ¶°, ®‰§§
I  J
J •B
J ¨O
R ™∫ ideal.
¶”•Bß⁄≠ö≥
(
R/
I)/(
J/
I)
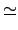 R
R/
J.
µ˝ ©˙.
•Ù§@
R/
I ™∫ ideal ≥£¨O
J/
I ≥o∫ÿߌ¶°§w¶b Corollary
6.3.7
√“±o. ¶”
(
R/
I)/(
J/
I)
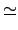 R
R/
J
•i•— Theorem
6.4.5 ™Ω±µ±o®Ï. §]¥N¨O•N:
R' =
R/
I,
J' =
J/
I •B¶“º

:
R R
R/
I, ≤≈¶X

(
a) =

. ¶πÆ…•i±o
J = {
a  R
R |

(
a)
 J'
J'}.
¨G•—
R/
J  R'
R'/
J' ±o√“.




§U§@≠∂: ØSÆÌ™∫ Ideals
§W§@≠∂: §§Ø≈ Ring ™∫© ΩË
´e§@≠∂: Ring Homomorphism
Administrator
2005-06-18
![]() ªs≥y•H§U™∫®Áº∆:
ªs≥y•H§U™∫®Áº∆:
![]() ¨O§@≠” ring homomorphism: πÔ•Ù∑N™∫
¨O§@≠” ring homomorphism: πÔ•Ù∑N™∫
![]() ,
,
![]()
![]() R/ker(
R/ker(![]() ), ß⁄≠ö≥
), ß⁄≠ö≥
![]() ¨O 1-1 •B onto.
≥o®‰πͧ£•≤√“§F(∑̵MßA≠n¶h¶π§@¡|§]®S√ˆ´Y), ¶]¨∞ß⁄≠öb Theorem
2.6.1 §w√“πL
¨O 1-1 •B onto.
≥o®‰πͧ£•≤√“§F(∑̵MßA≠n¶h¶π§@¡|§]®S√ˆ´Y), ¶]¨∞ß⁄≠öb Theorem
2.6.1 §w√“πL ![]() ≥o≠”®Áº∆¶b•[™k¨ð¶®¨O group homomorphism
§w∏g¨O 1-1 •B onto.
≥o≠”®Áº∆¶b•[™k¨ð¶®¨O group homomorphism
§w∏g¨O 1-1 •B onto.
![]() ¨O§@≠”±q
G/ker(
¨O§@≠”±q
G/ker(![]() ) ®Ï
im(
) ®Ï
im(![]() ) ™∫
isomorphism. ©“•H
G/ker(
) ™∫
isomorphism. ©“•H
G/ker(![]() )
) ![]() im(
im(![]() ).
).
![]()
![]() ¨O onto. ®∫ªÚß⁄≠Ùæ
im(
¨O onto. ®∫ªÚß⁄≠Ùæ
im(![]() ) = R'.
¶]¶πß⁄≠ö≥•H§U™∫§Þ≤z:
) = R'.
¶]¶πß⁄≠ö≥•H§U™∫§Þ≤z:
![]() N ¨O H ™∫
normal subgroup, •B
H/(H
N ¨O H ™∫
normal subgroup, •B
H/(H ![]() N)
N) ![]() (H . N)/N. ¶n≤¶bß⁄≠Ãß‚
group ¥´¶® ring, subgroup ¥´¶® subring, normal subgroup ¥´¶® ideal,
≥ô·ßOß—§F±N≠ºßÔ¨∞•[.
(H . N)/N. ¶n≤¶bß⁄≠Ãß‚
group ¥´¶® ring, subgroup ¥´¶® subring, normal subgroup ¥´¶® ideal,
≥ô·ßOß—§F±N≠ºßÔ¨∞•[.
![]() : S
: S![]() (S + I)/I,
®‰§§πÔ©“¶≥™∫ s
(S + I)/I,
®‰§§πÔ©“¶≥™∫ s ![]() S ß⁄≠ö≥
S ß⁄≠ö≥
![]() (s) =
(s) = ![]() .
.
![]() ¨O§@≠” ring homomorphism. ®∆πͧWπÔ•Ù∑N™∫ s, s'
¨O§@≠” ring homomorphism. ®∆πͧWπÔ•Ù∑N™∫ s, s' ![]() S, ß⁄≠ö≥
S, ß⁄≠ö≥
![]() : S
: S![]() (S + I)/I ¨O onto.
¶]¶π•i•H•Œ First Isomorphism Theorem (Corollary 6.4.3) ±o®Ï
(S + I)/I ¨O onto.
¶]¶π•i•H•Œ First Isomorphism Theorem (Corollary 6.4.3) ±o®Ï
![]() ¨O ring homomorphism ™æ
¨O ring homomorphism ™æ
![]() : R
: R![]() R'/J' ¨O§@≠”
onto ™∫ ring homomorphism, ß⁄≠öA¶∏•Œ First Isomorphism Theorem ™æ
R'/J' ¨O§@≠”
onto ™∫ ring homomorphism, ß⁄≠öA¶∏•Œ First Isomorphism Theorem ™æ
![]() : R
: R![]() R/I ¨O©w∏q¶®
R/I ¨O©w∏q¶®
![]() (a) =
(a) = ![]() ≥o≠” onto ™∫ ring homomorphism. •Ù∑N R/I
§§™∫ ideal J' •—´e Corollary 6.3.7 ™æ¨O•— R §§™∫¨Y§@
ideal J ßQ•Œ
≥o≠” onto ™∫ ring homomorphism. •Ù∑N R/I
§§™∫ ideal J' •—´e Corollary 6.3.7 ™æ¨O•— R §§™∫¨Y§@
ideal J ßQ•Œ ![]() ±o®Ï: §]¥N¨Oª°
J' =
±o®Ï: §]¥N¨Oª°
J' = ![]() (J) = J/I. ¨G•— Theorem
6.4.5 ß⁄≠ö≥•H§U™∫©w≤z(¶≥™∫Æ—¨O∫Ÿ≥o≠”¨∞ Third Isomorphism
Theorem.)
(J) = J/I. ¨G•— Theorem
6.4.5 ß⁄≠ö≥•H§U™∫©w≤z(¶≥™∫Æ—¨O∫Ÿ≥o≠”¨∞ Third Isomorphism
Theorem.)