


下一頁: Correspondence Theorem
上一頁: 中級 Group 的性質
前一頁: Group Homomorphisms
給定 G 和 G' 要說明它們是 isomorphic 時,
若想真正找到它們之間一個具體的 isomorphism 一般來說並不容易.
在這一節中我們將介紹三個定理來幫助我們確認
G  G'
而不必真正找到一個 isomorphism. 別害怕! 雖然是三個定理,
不過後兩個定理可以利用第一個定理輕鬆推得. 所以大家務必要學好第一個
isomorphism 定理.
G'
而不必真正找到一個 isomorphism. 別害怕! 雖然是三個定理,
不過後兩個定理可以利用第一個定理輕鬆推得. 所以大家務必要學好第一個
isomorphism 定理.
Theorem 2.6.1 (First Isomorphism Theorem)
若

:
G G'
G' 是一個 group homomorphism, 則
証 明.
首先我們回顧一下: 因

:
G G'
G' 是一個 group homomorphism, 由
Lemma
2.5.4 知
im(

) 是
G' 的 subgroup, 而
ker(

) 是
G 的 normal subgroup. 所以要證得這一個定理,
我們必須先在
G/ker(

) 這一個 quotient group 和
im(

)
這個 group 之間找到一個函數. 再說明這個函數是 group homomorphism,
最後再驗證它是 1-1 且 onto.
G/ker( ) 和
im(
) 和
im( ) 長甚麼樣子我們都不知道,
如何能無中生有創造出一個函數呢? 當然不可能無中生有!
我們可以用已經有的函數來創造它. 別忘了在假設中有一個
) 長甚麼樣子我們都不知道,
如何能無中生有創造出一個函數呢? 當然不可能無中生有!
我們可以用已經有的函數來創造它. 別忘了在假設中有一個  ,
我們可以利用
,
我們可以利用  製造以下的函數:
製造以下的函數:

:
G/ker(

)
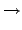
im(

);
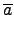
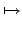

(
a),
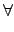
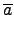
 G
G/ker(

).
具體來說

是把和
a 同類的元素送到

(
a)
這個值. 先別急著驗證

是一個 group homomorphism. 你確定

是一個`好函數' (well defined function) 嗎?
別忘了要成為一個好函數必須有以下兩個要素:(1)
每一個定義域裡的元素都必須送到對應域裡; (2) 不可以``一對多'':
也就是同一個元素不可以有兩種送法. 關於 (1) 我們的函數

是 O.K.
的. 因為每個定義域 (即
G/ker(

)) 裡的元素都是長

這個樣子, 其中
a  G
G. 所以

把

送到

(
a). 依定義

(
a) 當然在對應域
im(

) 內. 至於 (2)
就需要驗證了. 這是因為
G/ker(

) 內的元素並沒有唯一的方法用
G
中的元素表示出來. 也就是說在
G 中可以找到兩個不同的元素
a,
b
使得

和
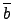
在
G/ker(

) 中是相同的.
所以要說明

不是一對多, 我們必須說明

(
a) =

(
b). 雖然
a b
b, 不過由

=
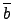
知
a 和
b 在以
ker(

) 這個 subgroup 的分類下是同類的. 別忘了
a 和
b
同類表示
a-1 . b 
ker(

). 也就是說

(
a-1 . b) =
e'. 再利用

是 group homomorphism 的假設, 我們得

(
a)
-1 . 
(
b) =

(
a-1 . b) =
e'.
等式兩邊乘上

(
a), 可得

(
a) =

(
b). 所以我們製造的

是一個 well
defined function.
接下來證  是一個 group homomorphism: 這不難, 只要記住
G/ker(
是一個 group homomorphism: 這不難, 只要記住
G/ker( ) 中的乘法是定義成:
) 中的乘法是定義成:
 .
. 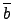 =
= 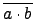 . 因此對任意的
. 因此對任意的
 ,
,
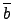
 G/ker(
G/ker( ), 我們有
), 我們有
另一方面因為

是 group homomorphism,
所以

(
a . b) =

(
a)
. 
(
b) =

(
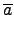
)
. 
(
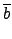
).
結合以上二式, 我們可得

(
 .
. 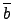
) =

(

)
. 
(
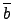
).
證明  是 onto 純粹是定義: 給定任意元素
y
是 onto 純粹是定義: 給定任意元素
y  im(
im( ),
依定義知存在 x
),
依定義知存在 x  G 使得 y =
G 使得 y =  (x). 因此我們可找
(x). 因此我們可找
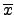
 G/ker(
G/ker( ) 代入
) 代入  得
得
 (
(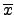 ) =
) =  (x) = y. 因此
(x) = y. 因此  是 onto.
是 onto.
既然  是 group homomorphism, 我們可以利用 Lemma 2.5.6:
也就是證明
ker(
是 group homomorphism, 我們可以利用 Lemma 2.5.6:
也就是證明
ker( ) 是
G/ker(
) 是
G/ker( ) 的 identity. 別忘了
G/ker(
) 的 identity. 別忘了
G/ker( ) 的 identity 是
) 的 identity 是
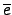 . 假設
. 假設
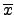
 ker(
ker( ), 即
), 即
 (
(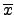 ) = e', 其中 e'
是 G' 的 identity. 但是由
) = e', 其中 e'
是 G' 的 identity. 但是由  的定義:
的定義:
 (
(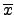 ) =
) =  (x), 故知
x
(x), 故知
x  ker(
ker( ). 然而 G
中元素用
ker(
). 然而 G
中元素用
ker( ) 來分類的話 x 和 e 是同類的 (因
e-1 . x = x
) 來分類的話 x 和 e 是同類的 (因
e-1 . x = x  ker(
ker( )). 故在
G/ker(
)). 故在
G/ker( ) 中
) 中
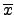 =
= 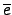 .
.
總結: 我們證得了  是一個從
G/ker(
是一個從
G/ker( ) 到
im(
) 到
im( ) 的
isomorphism. 所以
G/ker(
) 的
isomorphism. 所以
G/ker( )
)  im(
im( ).
).

當然了如果定理中的  是 onto. 那麼我們知
im(
是 onto. 那麼我們知
im( ) = G'.
因此我們有以下的引理:
) = G'.
因此我們有以下的引理:
First Isomorphism Theorem 告訴我們甚麼呢? 如果有一個 group G, 而
N 是其 normal subgroup. 則當我們要證明另一個 group G' 和 G/N
是 isomorphic 時. 我們不必辛苦的去找 G/N 和 G' 間的 isomorphism.
我們只要去找到一個 G 到 G' 的 epimorphism,  , 如果又剛好
ker(
, 如果又剛好
ker( ) = N. 那麼由 First Isomorphism Theorem 我們就可知
G/N
) = N. 那麼由 First Isomorphism Theorem 我們就可知
G/N  G' 了.
G' 了.
讓我們就利用證明第二個 isomorphism 定理來說明 First Isomorphism
Theorem 的妙用吧! 給定一 group G, 若 H, N 是 G 的 subgroups,
考慮以下之集合:
H . N = {
h . n |
h  H
H,
n  N
N}.
因為
H 和 N 都在 G 中所以 H . N 當然是 G 的一個子集合.
不過它不一定是 G 的 subgroup 喔! 主要的問題出在封閉性. 在 H . N 中任取兩元素, h . n 和
h' . n', 其中 h, h'  H,
n, n'
H,
n, n'  N. 則
(h . n) . (h' . n') 不一定可以寫成一個 H
中的元素乘上一個 N 中的元素這樣的形式. 不過若 H 和 N
其中一個是 G 的 normal subgroup, 那麼 H . N 就是 G 的
subgroup 了. 我們就把這個事實寫成 Lemma 吧!
N. 則
(h . n) . (h' . n') 不一定可以寫成一個 H
中的元素乘上一個 N 中的元素這樣的形式. 不過若 H 和 N
其中一個是 G 的 normal subgroup, 那麼 H . N 就是 G 的
subgroup 了. 我們就把這個事實寫成 Lemma 吧!
Lemma 2.6.3
若
H 是
G 的 subgroup 且
N 是
G 的 normal subgroup. 則
H . N =
N . H 且是
G 的 subgroup.
証 明.
因為
N 是
G 的 normal subgroup, 故因
H  G
G, 對於所有
h  H
H 及
n  N
N,
h . n . h-1  N
N. 換句話說存在
n'  N
N 使得
h . n . h-1 =
n'. 因此
h . n =
n' . h.
由此可得
H . N  N . H
N . H. 同理可得
N . H  H . N
H . N.
利用以上的結果, 前面所提的封閉性就可以解決了. 因為存在 n''  N
使得
h' . n' = n'' . h' 故
N
使得
h' . n' = n'' . h' 故
(h . n) . (h' . n') = (h . n) . (n'' . h') = h . (n . n'') . h'.
又因
n . n''  N
N, 故存在
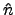
 N
N 使得
(
n . n'')
. h' =
h' . 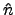
. 故
(
h . n)
. (
h' . n') = (
h . h')
. 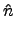
 H . N
H . N.
反元素的存在也可用相同的看法: 若
h . n  H . N, 則
H . N, 則
(
h . n)
-1 =
n-1 . h-1  N . H
N . H.
又
N . H =
H . N, 故
(
h . n)
-1  H . N
H . N.

現在讓我們看看第二個 isomorphism 定理在談甚麼?
Theorem 2.6.4 (Second Isomorphism Theorem)
若
H 是
G 的 subgroup 且
N 是
G 的 normal subgroup. 則
H  N
N 是
H 的 normal subgroup, 且
H/(
H 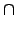 N
N)
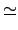
(
H . N)/
N.
証 明.
雖然定理提到
H  N
N 是
H 的 normal subgroup, 不過我們先不證它,
而直接用 first isomorphism 定理, normal subgroup 的部分會自然成立.
另外要注意的是定理中有另一個 quotient group
(
H . N)/
N.
前面提到這是一個 group 非得要
N 在
H . N 中 normal,
為甚麼定理不談
N 在
H . N 中 normal 呢?
學代數到現在你應該了解這是很 trivial 的事實了. 因為
H 中有
identity 故對任意的
n  N
N 皆可寫成
n =
e . n  H . N
H . N.
因此得
N  H . N
H . N. 換句話說
H 是
H . N 的
subgroup. 那為甚麼 normal? 既然
N 在
G 中 normal,
當然對任意的元素
g  H . N
H . N  G
G 都有
g . N . g-1 =
N 了.
怎麼用 first isomorphism 定理呢? 前面提到你要證明一個 quotient group
和另一個 group 是 isomorphism 時, 可以先不管 quotient group
中那個在底下的 normal subgroup. 在目前的情況我們有兩種選擇: (1) 從
H 到
(H . N)/N 的 homomorphism; (2) 從 H . N 到
H/(H  N) 的 homomorphism. 你會選哪一個呢? 當然是 (1) 了!
主要原因不只是 (2) 中的 H
N) 的 homomorphism. 你會選哪一個呢? 當然是 (1) 了!
主要原因不只是 (2) 中的 H  N 在 H 中 normal 還沒證.
更重要的是從 H 到
(H . N)/N 的 homomorphism 比 從 H . N
到
H/(H
N 在 H 中 normal 還沒證.
更重要的是從 H 到
(H . N)/N 的 homomorphism 比 從 H . N
到
H/(H  N) 的 homomorphism 更自然更好找. (為甚麼呢?
只能說是憑感覺吧!)
N) 的 homomorphism 更自然更好找. (為甚麼呢?
只能說是憑感覺吧!)
讓我們先找一個從 H 到
(H . N)/N 的函數吧! 因為 H 是 H . N 的 subgroup, 我們有一個很自然的映射把 H 的元素送到 H . N:
也就是把 H 中的元素乖乖的原封不動的放到 H . N 中. 即
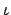 : H
: H H . N 其中
H . N 其中
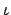 (h) = h. 又 N 在 H . N 中
normal, 我們又有一個很自然的可將 H . N 的元素用 N 分類的函數.
即
(h) = h. 又 N 在 H . N 中
normal, 我們又有一個很自然的可將 H . N 的元素用 N 分類的函數.
即
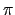 : H . N
: H . N (H . N)/N 其中對所有的
g
(H . N)/N 其中對所有的
g  H . N
我們有
H . N
我們有
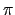 (g) =
(g) =  . 將
. 將 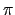 和
和 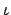 合成,
我們自然有一個函數
合成,
我們自然有一個函數
其中對所有的
h  H
H 我們有
現在要證  是一個 group homomorphism. (我們不必證
是一個 group homomorphism. (我們不必證  是
well defined, 這是因為
是
well defined, 這是因為  這個函數`明明白白'的把 h 送到
這個函數`明明白白'的把 h 送到
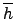 這一個元素. 沒有前面那種一對多的可能.) 事實上對任意的
h, h'
這一個元素. 沒有前面那種一對多的可能.) 事實上對任意的
h, h'  H, 我們有
H, 我們有

(
h . h') =
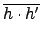
=
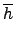 .
. 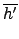
=

(
h)
. 
(
h').
接下來證  是 onto. 任意的 H . N 中的元素可寫成 h . n, 其中 h
是 onto. 任意的 H . N 中的元素可寫成 h . n, 其中 h  H, n
H, n  N. 所以任意的
(H . N)/N
中的元素都可寫成
N. 所以任意的
(H . N)/N
中的元素都可寫成
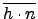 . 但是
. 但是
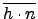 =
= 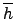 .
. 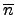 . 別忘了我們是用 N 來分類所以 N
中的元素都和 identity 同類. 也就是說
. 別忘了我們是用 N 來分類所以 N
中的元素都和 identity 同類. 也就是說
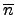 =
= 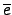 .
因此
.
因此
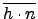 =
= 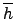 . 由此知任意
(H . N)/N
中的元素
. 由此知任意
(H . N)/N
中的元素
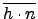 我們都可找 h
我們都可找 h  H 使得
H 使得
 (h) =
(h) = 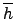 =
= 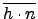 . 因此
. 因此  是 onto.
是 onto.
既然  是一個從 H 到
(H . N)/N 的 epimorphism,
我們可以用 First Isomorphism Theorem (Corollary 2.6.2) 得到
是一個從 H 到
(H . N)/N 的 epimorphism,
我們可以用 First Isomorphism Theorem (Corollary 2.6.2) 得到
H/ker(

)
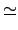
(
H . N)/
N.
甚麼是
ker(

) 呢? 依定義
ker(

) 是
H 中的元素
h 使得

(
h) 是
(
H . N)/
N 的
identity,
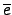
. 也就是說

(
h) =
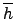
=
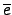
. 別忘了
(
H . N)/
N
中的元素是對
N 分類, 故
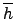
=
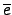
表示
h 和
e 同類, 也就是說
e-1 . h =
h  N
N. 由此知
ker(

)
的元素既要在
H 中也要在
N 中; 換句話說
ker(

)
 H
H  N
N. 反之若
a  H
H  N
N, 則因
a  N
N 得

(
a) =

=
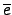
. 故
H  N
N 
ker(

). 由此知
ker(

) =
H  N
N. 因此我們由 Lemma
2.5.4 知
H  N
N 是
H 的 normal subgroup 也由 First
Isomorphism Theorem 知
H/(
H 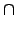 N
N)
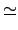
(
H . N)/
N.

相信大家已經看出 First Isomorphism Theorem 的妙用了.
讓我們再用它來證第三個 isomorphism 定理吧!
Theorem 2.6.5 (Third Isomorphism Theorem)
若

:
G G'
G' 是一個 group epimorphism. 假設
N' 是
G' 的一個
normal subgroup. 令
則
N 是
G 的 normal subgroup 且
G/
N 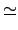 G'
G'/
N'.
証 明.
令
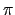
:
G' G'
G'/
N' 是
G' 對
N' 來分類的函數.
如前一定理的證明我們可定

=
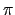 o
o
:
G G'
G'/
N'. 也就是說

(
a) =
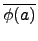
,
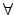 a
a  G
G.
由  是 group homomorphism 知
是 group homomorphism 知

(
a . b) =
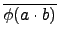
=
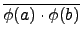
=
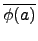 .
. 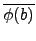
=

(
a)
. 
(
b).
故

是一個從
G 到
G'/
N' 的 group homomorphism.
任意 G'/N' 的元素都可寫成
 其中 g
其中 g  G' 這種形式.
但因
G' 這種形式.
但因  是 onto, 故存在 a
是 onto, 故存在 a  G 使得
G 使得  (a) = g. 所以
(a) = g. 所以
因此

也是
onto. (其實若同學了解一些合成函數的性質, 馬上可以利用兩個 onto
的函數其合成函數也是 onto 知

是 onto.)
既然知
 : G
: G G'/N' 是一個 epimorphism, 我們再次用 First
Isomorphism Theorem 知
G'/N' 是一個 epimorphism, 我們再次用 First
Isomorphism Theorem 知
G/ker(

)
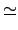 G'
G'/
N'.
甚麼是
ker(

) 呢? 若
a 
ker(

) 即

(
a) =
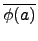
=
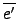
, 其中
e' 是
G' 的
identity. 也就是說

(
a) 和
e' 在用
N' 的分類下是同類的.
所以

(
a)
 N'
N'. 由
N 的定義知, 這表示
a  N
N. 故
ker(

)
 N
N. 另外若
a  N
N, 則

(
a)
 N'
N' 故在
G'/
N 中

(
a) =
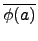
=
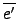
, 因此
a 
ker(

). 得
N 
ker(

). 也就是說
ker(

) =
N
且
N 是
G 的 normal subgroup.




下一頁: Correspondence Theorem
上一頁: 中級 Group 的性質
前一頁: Group Homomorphisms
Administrator
2005-06-18
![]() G'
而不必真正找到一個 isomorphism. 別害怕! 雖然是三個定理,
不過後兩個定理可以利用第一個定理輕鬆推得. 所以大家務必要學好第一個
isomorphism 定理.
G'
而不必真正找到一個 isomorphism. 別害怕! 雖然是三個定理,
不過後兩個定理可以利用第一個定理輕鬆推得. 所以大家務必要學好第一個
isomorphism 定理.
![]() ) 和
im(
) 和
im(![]() ) 長甚麼樣子我們都不知道,
如何能無中生有創造出一個函數呢? 當然不可能無中生有!
我們可以用已經有的函數來創造它. 別忘了在假設中有一個
) 長甚麼樣子我們都不知道,
如何能無中生有創造出一個函數呢? 當然不可能無中生有!
我們可以用已經有的函數來創造它. 別忘了在假設中有一個 ![]() ,
我們可以利用
,
我們可以利用 ![]() 製造以下的函數:
製造以下的函數:
![]() 是一個 group homomorphism: 這不難, 只要記住
G/ker(
是一個 group homomorphism: 這不難, 只要記住
G/ker(![]() ) 中的乘法是定義成:
) 中的乘法是定義成:
![]() .
. ![]() =
= ![]() . 因此對任意的
. 因此對任意的
![]() ,
,
![]()
![]() G/ker(
G/ker(![]() ), 我們有
), 我們有
![]() 是 onto 純粹是定義: 給定任意元素
y
是 onto 純粹是定義: 給定任意元素
y ![]() im(
im(![]() ),
依定義知存在 x
),
依定義知存在 x ![]() G 使得 y =
G 使得 y = ![]() (x). 因此我們可找
(x). 因此我們可找
![]()
![]() G/ker(
G/ker(![]() ) 代入
) 代入 ![]() 得
得
![]() (
(![]() ) =
) = ![]() (x) = y. 因此
(x) = y. 因此 ![]() 是 onto.
是 onto.
![]() 是 group homomorphism, 我們可以利用 Lemma 2.5.6:
也就是證明
ker(
是 group homomorphism, 我們可以利用 Lemma 2.5.6:
也就是證明
ker(![]() ) 是
G/ker(
) 是
G/ker(![]() ) 的 identity. 別忘了
G/ker(
) 的 identity. 別忘了
G/ker(![]() ) 的 identity 是
) 的 identity 是
![]() . 假設
. 假設
![]()
![]() ker(
ker(![]() ), 即
), 即
![]() (
(![]() ) = e', 其中 e'
是 G' 的 identity. 但是由
) = e', 其中 e'
是 G' 的 identity. 但是由 ![]() 的定義:
的定義:
![]() (
(![]() ) =
) = ![]() (x), 故知
x
(x), 故知
x ![]() ker(
ker(![]() ). 然而 G
中元素用
ker(
). 然而 G
中元素用
ker(![]() ) 來分類的話 x 和 e 是同類的 (因
e-1 . x = x
) 來分類的話 x 和 e 是同類的 (因
e-1 . x = x ![]() ker(
ker(![]() )). 故在
G/ker(
)). 故在
G/ker(![]() ) 中
) 中
![]() =
= ![]() .
.
![]() 是一個從
G/ker(
是一個從
G/ker(![]() ) 到
im(
) 到
im(![]() ) 的
isomorphism. 所以
G/ker(
) 的
isomorphism. 所以
G/ker(![]() )
) ![]() im(
im(![]() ).
).
![]()
![]() 是 onto. 那麼我們知
im(
是 onto. 那麼我們知
im(![]() ) = G'.
因此我們有以下的引理:
) = G'.
因此我們有以下的引理:
![]() , 如果又剛好
ker(
, 如果又剛好
ker(![]() ) = N. 那麼由 First Isomorphism Theorem 我們就可知
G/N
) = N. 那麼由 First Isomorphism Theorem 我們就可知
G/N ![]() G' 了.
G' 了.
![]() N
使得
h' . n' = n'' . h' 故
N
使得
h' . n' = n'' . h' 故
![]() H . N, 則
H . N, 則
![]() N) 的 homomorphism. 你會選哪一個呢? 當然是 (1) 了!
主要原因不只是 (2) 中的 H
N) 的 homomorphism. 你會選哪一個呢? 當然是 (1) 了!
主要原因不只是 (2) 中的 H ![]() N 在 H 中 normal 還沒證.
更重要的是從 H 到
(H . N)/N 的 homomorphism 比 從 H . N
到
H/(H
N 在 H 中 normal 還沒證.
更重要的是從 H 到
(H . N)/N 的 homomorphism 比 從 H . N
到
H/(H ![]() N) 的 homomorphism 更自然更好找. (為甚麼呢?
只能說是憑感覺吧!)
N) 的 homomorphism 更自然更好找. (為甚麼呢?
只能說是憑感覺吧!)
![]() : H
: H![]() H . N 其中
H . N 其中
![]() (h) = h. 又 N 在 H . N 中
normal, 我們又有一個很自然的可將 H . N 的元素用 N 分類的函數.
即
(h) = h. 又 N 在 H . N 中
normal, 我們又有一個很自然的可將 H . N 的元素用 N 分類的函數.
即
![]() : H . N
: H . N![]() (H . N)/N 其中對所有的
g
(H . N)/N 其中對所有的
g ![]() H . N
我們有
H . N
我們有
![]() (g) =
(g) = ![]() . 將
. 將 ![]() 和
和 ![]() 合成,
我們自然有一個函數
合成,
我們自然有一個函數
![]() 是一個 group homomorphism. (我們不必證
是一個 group homomorphism. (我們不必證 ![]() 是
well defined, 這是因為
是
well defined, 這是因為 ![]() 這個函數`明明白白'的把 h 送到
這個函數`明明白白'的把 h 送到
![]() 這一個元素. 沒有前面那種一對多的可能.) 事實上對任意的
h, h'
這一個元素. 沒有前面那種一對多的可能.) 事實上對任意的
h, h' ![]() H, 我們有
H, 我們有
![]() 是 onto. 任意的 H . N 中的元素可寫成 h . n, 其中 h
是 onto. 任意的 H . N 中的元素可寫成 h . n, 其中 h ![]() H, n
H, n ![]() N. 所以任意的
(H . N)/N
中的元素都可寫成
N. 所以任意的
(H . N)/N
中的元素都可寫成
![]() . 但是
. 但是
![]() =
= ![]() .
. ![]() . 別忘了我們是用 N 來分類所以 N
中的元素都和 identity 同類. 也就是說
. 別忘了我們是用 N 來分類所以 N
中的元素都和 identity 同類. 也就是說
![]() =
= ![]() .
因此
.
因此
![]() =
= ![]() . 由此知任意
(H . N)/N
中的元素
. 由此知任意
(H . N)/N
中的元素
![]() 我們都可找 h
我們都可找 h ![]() H 使得
H 使得
![]() (h) =
(h) = ![]() =
= ![]() . 因此
. 因此 ![]() 是 onto.
是 onto.
![]() 是一個從 H 到
(H . N)/N 的 epimorphism,
我們可以用 First Isomorphism Theorem (Corollary 2.6.2) 得到
是一個從 H 到
(H . N)/N 的 epimorphism,
我們可以用 First Isomorphism Theorem (Corollary 2.6.2) 得到
![]() 是 group homomorphism 知
是 group homomorphism 知
![]() 其中 g
其中 g ![]() G' 這種形式.
但因
G' 這種形式.
但因 ![]() 是 onto, 故存在 a
是 onto, 故存在 a ![]() G 使得
G 使得 ![]() (a) = g. 所以
(a) = g. 所以
![]() : G
: G![]() G'/N' 是一個 epimorphism, 我們再次用 First
Isomorphism Theorem 知
G'/N' 是一個 epimorphism, 我們再次用 First
Isomorphism Theorem 知
![]()