

下一頁: Modulo 2pn 的 Primitive
上一頁: The Primitive Root Theorem
前一頁: Modulo p2 的 primitive
由於 modulo p 的 primitive root 存在, 利用
Corollary 6.1.9 知在 modulo p 之下共有
 (
( (p)) =
(p)) =  (p - 1) 個 primitive roots. Proposition
6.3.5 告訴我們每一個 modulo p 的 primitive root 在 modulo
p2 之下可得 p - 1 個 primitive roots, 所以在 modulo p2
之下我們共找到了
(p - 1)
(p - 1) 個 primitive roots. Proposition
6.3.5 告訴我們每一個 modulo p 的 primitive root 在 modulo
p2 之下可得 p - 1 個 primitive roots, 所以在 modulo p2
之下我們共找到了
(p - 1) (p - 1) 個 primitive roots. 然而由於
modulo p2 的 primitive root 存在, Corollary 6.1.9
告訴我們在 modulo p2 之下共有
(p - 1) 個 primitive roots. 然而由於
modulo p2 的 primitive root 存在, Corollary 6.1.9
告訴我們在 modulo p2 之下共有
 (
( (p2)) =
(p2)) =  (p(p - 1)) 個
primitive roots. 由於 p 和 p - 1 互質, 我們有
(p(p - 1)) 個
primitive roots. 由於 p 和 p - 1 互質, 我們有
 (
( (p2)) =
(p2)) =  (p)
(p) (p - 1) = (p - 1)
(p - 1) = (p - 1) (p - 1). 此值恰與前面由
modulo p 的 primitive root 所得 modulo p2 的 primitive roots
的個數相吻合. 也就是說每一個 modulo p2 的 primitive root
確來自於某個 modulo p 的 primitive root. 我們可以如此一直估算下去,
若 modulo p3 的 primitive root 存在, 則由 Corollary 6.1.9
知在 modulo p3 之下共有
(p - 1). 此值恰與前面由
modulo p 的 primitive root 所得 modulo p2 的 primitive roots
的個數相吻合. 也就是說每一個 modulo p2 的 primitive root
確來自於某個 modulo p 的 primitive root. 我們可以如此一直估算下去,
若 modulo p3 的 primitive root 存在, 則由 Corollary 6.1.9
知在 modulo p3 之下共有
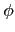
(
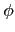
(
p3)) =
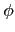
(
p2(
p - 1)) =
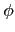
(
p2)
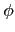
(
p - 1) =
p(
p - 1)
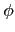
(
p - 1)
個 primitive roots. 而又已知在 modulo p2 之下共有
(p - 1) (p - 1) 個 primitive roots. 每一個 modulo p2 的
primitive root, 在 modulo p3 之下共可產生 p 個不同餘類, 所以這
(p - 1)
(p - 1) 個 primitive roots. 每一個 modulo p2 的
primitive root, 在 modulo p3 之下共可產生 p 個不同餘類, 所以這
(p - 1) (p - 1) 個 modulo p2 的 primitive roots 在 modulo p3
之下共產生了
p(p - 1)
(p - 1) 個 modulo p2 的 primitive roots 在 modulo p3
之下共產生了
p(p - 1) (p - 1) 個不同餘類. 這個數字恰與前面所提若
modulo p3 的 primitive root 存在則在 modulo p3 之下共有
p(p - 1)
(p - 1) 個不同餘類. 這個數字恰與前面所提若
modulo p3 的 primitive root 存在則在 modulo p3 之下共有
p(p - 1) (p - 1) 個 primitive roots 相吻合. 也就是說每一個 modulo
p2 的 primitive root, 在 modulo p3 之下產生的 p
個不同餘類``應該''在 modulo p3 仍為 primitive root.
(p - 1) 個 primitive roots 相吻合. 也就是說每一個 modulo
p2 的 primitive root, 在 modulo p3 之下產生的 p
個不同餘類``應該''在 modulo p3 仍為 primitive root.
接下來我們就是要用數學歸納法來驗證此事, 我們要證明當 n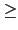 3 時
任何數只要在 modulo p2 是 primitive root, 則在 modulo pn
必也是 primitive root. 首先我們來看如何判別一個 modulo pn 的
primitive root 在 modulo pn + 1 之下是否為 primitive root.
3 時
任何數只要在 modulo p2 是 primitive root, 則在 modulo pn
必也是 primitive root. 首先我們來看如何判別一個 modulo pn 的
primitive root 在 modulo pn + 1 之下是否為 primitive root.
Lemma 6.3.6
假設
a 
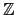
是一個 primitive root modulo
pn. 則
ord
pn + 1(
a) =
pn - 1(
p - 1) 或
ord
pn + 1(
a) =
pn(
p - 1).
特別地,
apn - 1(p - 1) 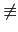
1(mod
pn + 1) 若且唯若
a 在
modulo
pn + 1 之下是一個 primitive root.
証 明.
依假設
a 在 modulo
pn 之下是 primitive root 表示
ord
pn(
a) =

(
pn) =
pn - 1(
p - 1). 現假設
ord
pn + 1(
a) =
k, 則
ak 
1(mod
pn + 1), 因此知
ak 
1(mod
pn). 故依
ord
pn(
a) =
pn - 1(
p - 1) 及
Proposition
6.1.4 知
pn - 1(
p - 1)|
k. 又因為
a 與
p 互質,
故
a 與
pn + 1 互質, 故由 Euler's Theorem 知
a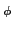 (pn + 1)
(pn + 1) 
1(mod
pn + 1), 因此在 modulo
pn + 1
的情況再利用 Proposition
6.1.4 知
k|

(
pn + 1). 由於

(
pn + 1) =
pn(
p - 1), 我們得
pn - 1(
p - 1)|
k 且
k|
pn(
p - 1).
也就是
k =
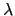 pn - 1
pn - 1(
p - 1) 且又
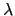 pn - 1
pn - 1(
p - 1)|
pn(
p - 1), 故知
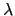
|
p. 因此由
p 是質數知
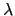
= 1 或
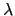
=
p. 故得證
ord
pn + 1(
a) =
pn - 1(
p - 1)
或
ord
pn + 1(
a) =
pn(
p - 1).
現若
apn - 1(p - 1) 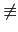 1(mod pn + 1), 知 a 在 modulo
pn + 1 之下其 order 一定不是
pn - 1(p - 1), 故得
ordpn + 1(a) = pn(p - 1) =
1(mod pn + 1), 知 a 在 modulo
pn + 1 之下其 order 一定不是
pn - 1(p - 1), 故得
ordpn + 1(a) = pn(p - 1) =  (pn + 1). 由 Corollary
6.1.7 得證 a 在 modulo pn + 1 之下是一個 primitive root.
反之若 a 在 modulo pn + 1 之下是 primitive root, 即
ordpn + 1(a) = pn(p - 1), 故由 order 的定義知
apn - 1(p - 1)
(pn + 1). 由 Corollary
6.1.7 得證 a 在 modulo pn + 1 之下是一個 primitive root.
反之若 a 在 modulo pn + 1 之下是 primitive root, 即
ordpn + 1(a) = pn(p - 1), 故由 order 的定義知
apn - 1(p - 1) 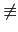 1(mod pn + 1).
1(mod pn + 1).
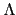
現若我們找到 a 在 modulo p2 之下是 primitive root, 要檢查 a
在 modulo p3 之下是否為 primitive root, 依 Lemma 6.3.6,
我們要檢查
ap(p - 1) 在 modulo p3 之下是否與 1 同餘.
然而已知
ap - 1  1(mod p) (Fermat's Little Theorem)
我們可令
ap - 1 = 1 +
1(mod p) (Fermat's Little Theorem)
我們可令
ap - 1 = 1 + 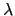 p. 此時由於 a 在 modulo p2 之下是
primitive root 故由 Lemma 6.3.4 知
ap - 1
p. 此時由於 a 在 modulo p2 之下是
primitive root 故由 Lemma 6.3.4 知
ap - 1 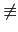 1(mod p2), 即
p
1(mod p2), 即
p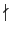
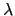 . 依此可得
. 依此可得
ap(p - 1) = (
ap - 1)
p = (1 +
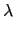 p
p)
p = 1 +
p(
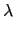 p
p) +
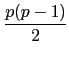
(
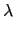 p
p)
2 +
... .
這裡由於 p 是奇數所以
p| p(p - 1)/2 (注意這就是為何此結果在 p = 2 時不成立的原因),
再加上之後每一項
Cpk(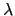 p)k, k
p)k, k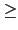 3 在 modulo p3
之下皆為 0, 所以我們得
3 在 modulo p3
之下皆為 0, 所以我們得
ap(p - 1) 
1 +
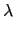 p2
p2(mod
p3).
故由
p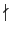
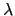 得證
ap(p - 1)
得證
ap(p - 1) 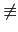 1(mod p3), 所以依 Lemma 6.3.6
知 a 在 modulo p3 之下亦為 primitive root. 如此一直下去,
我們可證得當 n
1(mod p3), 所以依 Lemma 6.3.6
知 a 在 modulo p3 之下亦為 primitive root. 如此一直下去,
我們可證得當 n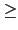 3 時, a 在 modulo pn 之下皆為 primitive
root.
3 時, a 在 modulo pn 之下皆為 primitive
root.
Proposition 6.3.7
假設
a 在 modulo
p2 之下是一個 primitive root. 則對任意
n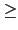
3,
a 在 modulo
pn 之下也是 primitive root.
証 明.
前面我們已證得
a 在 modulo
p3 之下是 primitive root.
現在依歸納法, 我們假設
a 在 modulo
pn (
n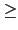
3) 之下是
primitive root, 要證明
a 在 modulo
pn + 1 之下仍為 primitive
root.
由於 a 與 p 互質, 依 Euler's Theorem 知
a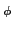 (pn - 1) = apn - 2(p - 1)
(pn - 1) = apn - 2(p - 1)  1(mod pn - 1). 現假設
apn - 2(p - 1) = 1 +
1(mod pn - 1). 現假設
apn - 2(p - 1) = 1 + 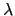 pn - 1. 由於 a 在 modulo pn
之下是 primitive root, 依 Lemma 6.3.6 知
apn - 2(p - 1)
pn - 1. 由於 a 在 modulo pn
之下是 primitive root, 依 Lemma 6.3.6 知
apn - 2(p - 1) 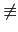 1(mod pn), 故知
p
1(mod pn), 故知
p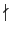
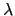 .
現考慮
.
現考慮
apn - 1(p - 1) = (
apn - 2(p - 1))
p = (1 +
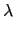 pn - 1
pn - 1)
p = 1 +
p(
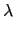 pn - 1
pn - 1) +
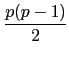
(
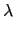 pn - 1
pn - 1)
2 +
... .
在
p(
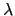 pn - 1
pn - 1) 之後每一項
Cpk(
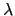 pn - 1
pn - 1)
k,
k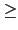
2 中由於
k(
n - 1)
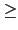
2(
n - 1) =
n + (
n - 2)
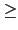 n
n + 1 (因為
n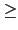
3), 所以當
k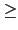
2 時在 modulo
pn + 1 之下
Cpk(
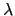 pn - 1
pn - 1)
k 皆為 0, 所以我們得
apn - 1(p - 1) 
1 +
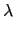 pn
pn(mod
pn + 1).
故由
p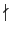
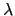
得證
apn - 1(p - 1) 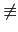
1(mod
pn + 1), 所以依 Lemma
6.3.6 知
a 在 modulo
pn + 1 之下亦為 primitive root.
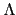
從 Theorem 6.3.3 以及 Proposition 6.3.5 我們知道 modulo
p2 的 primitive root 存在, 所以再由 Proposition
6.3.7 得知當 n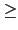 3 時 modulo pn 的 primitive root
也存在. 再次強調由於從 modulo p2 的 primitive root 推得 modulo
p3 的 primitive root 之過程需用到 p 是奇數所以當 n
3 時 modulo pn 的 primitive root
也存在. 再次強調由於從 modulo p2 的 primitive root 推得 modulo
p3 的 primitive root 之過程需用到 p 是奇數所以當 n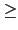 3 時
modulo pn 的 primitive root 存在需在 p 是奇質數才成立.
事實上之前我們已知在 modulo 23 = 8 時 primitive root 是不存在的.
3 時
modulo pn 的 primitive root 存在需在 p 是奇質數才成立.
事實上之前我們已知在 modulo 23 = 8 時 primitive root 是不存在的.


下一頁: Modulo 2pn 的 Primitive
上一頁: The Primitive Root Theorem
前一頁: Modulo p2 的 primitive
Li
2007-06-28
![]() 3 時
任何數只要在 modulo p2 是 primitive root, 則在 modulo pn
必也是 primitive root. 首先我們來看如何判別一個 modulo pn 的
primitive root 在 modulo pn + 1 之下是否為 primitive root.
3 時
任何數只要在 modulo p2 是 primitive root, 則在 modulo pn
必也是 primitive root. 首先我們來看如何判別一個 modulo pn 的
primitive root 在 modulo pn + 1 之下是否為 primitive root.
![]() 1(mod pn + 1), 知 a 在 modulo
pn + 1 之下其 order 一定不是
pn - 1(p - 1), 故得
ordpn + 1(a) = pn(p - 1) =
1(mod pn + 1), 知 a 在 modulo
pn + 1 之下其 order 一定不是
pn - 1(p - 1), 故得
ordpn + 1(a) = pn(p - 1) = ![]() (pn + 1). 由 Corollary
6.1.7 得證 a 在 modulo pn + 1 之下是一個 primitive root.
反之若 a 在 modulo pn + 1 之下是 primitive root, 即
ordpn + 1(a) = pn(p - 1), 故由 order 的定義知
apn - 1(p - 1)
(pn + 1). 由 Corollary
6.1.7 得證 a 在 modulo pn + 1 之下是一個 primitive root.
反之若 a 在 modulo pn + 1 之下是 primitive root, 即
ordpn + 1(a) = pn(p - 1), 故由 order 的定義知
apn - 1(p - 1) ![]() 1(mod pn + 1).
1(mod pn + 1).
![]()
![]() 1(mod p) (Fermat's Little Theorem)
我們可令
ap - 1 = 1 +
1(mod p) (Fermat's Little Theorem)
我們可令
ap - 1 = 1 + ![]() p. 此時由於 a 在 modulo p2 之下是
primitive root 故由 Lemma 6.3.4 知
ap - 1
p. 此時由於 a 在 modulo p2 之下是
primitive root 故由 Lemma 6.3.4 知
ap - 1 ![]() 1(mod p2), 即
p
1(mod p2), 即
p![]()
![]() . 依此可得
. 依此可得
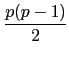 (
(![]() (pn - 1) = apn - 2(p - 1)
(pn - 1) = apn - 2(p - 1) ![]() 1(mod pn - 1). 現假設
apn - 2(p - 1) = 1 +
1(mod pn - 1). 現假設
apn - 2(p - 1) = 1 + ![]() pn - 1. 由於 a 在 modulo pn
之下是 primitive root, 依 Lemma 6.3.6 知
apn - 2(p - 1)
pn - 1. 由於 a 在 modulo pn
之下是 primitive root, 依 Lemma 6.3.6 知
apn - 2(p - 1) ![]() 1(mod pn), 故知
p
1(mod pn), 故知
p![]()
![]() .
現考慮
.
現考慮
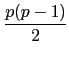 (
(![]() 3 時 modulo pn 的 primitive root
也存在. 再次強調由於從 modulo p2 的 primitive root 推得 modulo
p3 的 primitive root 之過程需用到 p 是奇數所以當 n
3 時 modulo pn 的 primitive root
也存在. 再次強調由於從 modulo p2 的 primitive root 推得 modulo
p3 的 primitive root 之過程需用到 p 是奇數所以當 n![]() 3 時
modulo pn 的 primitive root 存在需在 p 是奇質數才成立.
事實上之前我們已知在 modulo 23 = 8 時 primitive root 是不存在的.
3 時
modulo pn 的 primitive root 存在需在 p 是奇質數才成立.
事實上之前我們已知在 modulo 23 = 8 時 primitive root 是不存在的.