在 modulo p 時, 有一件事是很特殊的即 Theorem 4.1.3
告訴我們一個 n 次的整係數多項式在 modulo p 之下最多有 n 個解.
然而若 p![]() a 且
ordp(a) = n, 已知
a, a2,..., an 在 modulo
p 之下皆相異, 且由於
an
a 且
ordp(a) = n, 已知
a, a2,..., an 在 modulo
p 之下皆相異, 且由於
an ![]() 1(mod p), 故
(ai)n
1(mod p), 故
(ai)n ![]() 1(mod p). 由此可知
a, a2,..., an 這 n 個在 modulo p
之下皆不同餘的數皆為
xn
1(mod p). 由此可知
a, a2,..., an 這 n 個在 modulo p
之下皆不同餘的數皆為
xn ![]() 1(mod p) 的一個解, 但由於此式在
modulo p 之下至多有 n 個解, 所以它們就是
xn
1(mod p) 的一個解, 但由於此式在
modulo p 之下至多有 n 個解, 所以它們就是
xn ![]() 1(mod p)
所有的解. 另一方面, 若 p
1(mod p)
所有的解. 另一方面, 若 p![]() b 且
ordp(b) = n, 則由於 b 是
xn
b 且
ordp(b) = n, 則由於 b 是
xn ![]() 1(mod p) 之一解, 故由前知存在
i
1(mod p) 之一解, 故由前知存在
i ![]() {1,..., n} 使得
b
{1,..., n} 使得
b ![]() ai(mod p). 換言之, 所有在 modulo p 之下 order 為 n
的元素, 在 modulo p 之下必和
{a, a2,..., an} 中某個元素同餘,
故利用 Corollary 6.1.9 知在 modulo p 之下僅有
ai(mod p). 換言之, 所有在 modulo p 之下 order 為 n
的元素, 在 modulo p 之下必和
{a, a2,..., an} 中某個元素同餘,
故利用 Corollary 6.1.9 知在 modulo p 之下僅有 ![]() (n)
個元素其 order 為 n. 我們將此結果總結如下.
(n)
個元素其 order 為 n. 我們將此結果總結如下.
我們要說在 modulo p 之下有 primitive root 主要的方法便是將 modulo
p 之下的元素依其 order 分類. 最後說明 order 為
![]() (p) = p - 1
那一類元素所成的集合不是
(p) = p - 1
那一類元素所成的集合不是 ![]() (空集合).
下面就是依這樣分類所得之結果.
(空集合).
下面就是依這樣分類所得之結果.
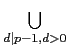 Sd = S.
Sd = S.
(2)
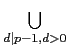 Sd 這個符號的意思是將所有 Sd
其中
d
Sd 這個符號的意思是將所有 Sd
其中
d ![]()
![]() 且 d| p - 1 聯集起來. 由於對所有 d| p - 1 皆有
Sd
且 d| p - 1 聯集起來. 由於對所有 d| p - 1 皆有
Sd ![]() S, 所以
S, 所以
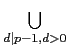 Sd
Sd ![]() S.
另一方面若 i
S.
另一方面若 i ![]() S, 由於 p
S, 由於 p![]() i, 故由 Theorem 3.3.4 知
ip - 1
i, 故由 Theorem 3.3.4 知
ip - 1 ![]() 1(mod p). 因此由 Proposition 6.1.4 知
ordp(i)| p - 1. 換句話說, 若
ordp(i) = d, 則 d| p - 1,
故知存在 d| p - 1 使得 i
1(mod p). 因此由 Proposition 6.1.4 知
ordp(i)| p - 1. 換句話說, 若
ordp(i) = d, 則 d| p - 1,
故知存在 d| p - 1 使得 i ![]() Sd. 得證
S
Sd. 得證
S ![]()
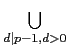 Sd, 因此知
Sd, 因此知
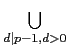 Sd = S.
Sd = S.
(3) 若
Sd![]()
![]() , 表示存在 a
, 表示存在 a ![]() Sd. 此時 p
Sd. 此時 p![]() a 且
ordp(a) = d, 故利用 Lemma 6.3.1 知在 modulo p 之下共有
a 且
ordp(a) = d, 故利用 Lemma 6.3.1 知在 modulo p 之下共有
![]() (d ) 個元素其 order 為 d. 由於 S 是 reduced residue system
modulo p, 這
(d ) 個元素其 order 為 d. 由於 S 是 reduced residue system
modulo p, 這 ![]() (d ) 個元素在 modulo p 之下必和 S 中
(d ) 個元素在 modulo p 之下必和 S 中
![]() (d ) 個元素同餘. 因此 S 中這
(d ) 個元素同餘. 因此 S 中這 ![]() (d ) 個元素剛好組成 Sd,
故知 Sd 共有
(d ) 個元素剛好組成 Sd,
故知 Sd 共有 ![]() (d ) 個元素.
(d ) 個元素.
![]()
Lemma 6.3.2(1,2) 告訴我們
S = {1, 2,..., p - 1}
中的每一個元素必會落在某個且恰有一個 Sd 中, 其中
d ![]()
![]() 且
d| p - 1. 因此若計算每個 Sd 中的元素個數再加總起來其值應為 S
中的元素個數 p - 1. 依此我們可以得到以下重要的結果.
且
d| p - 1. 因此若計算每個 Sd 中的元素個數再加總起來其值應為 S
中的元素個數 p - 1. 依此我們可以得到以下重要的結果.
由 Lemma 6.3.2(1,2) 我們知
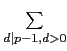 n(d )= p - 1
而且 Lemma 6.3.2(3) 告訴我們 n(d )= 0 或
n(d )=
n(d )= p - 1
而且 Lemma 6.3.2(3) 告訴我們 n(d )= 0 或
n(d )= ![]() (d ).
另一方面利用 Corollary 2.3.6 我們知
(d ).
另一方面利用 Corollary 2.3.6 我們知
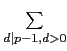
![]() (d )= p - 1, 而
(d )= p - 1, 而 ![]() (d ) > 0, 故比較
(d ) > 0, 故比較
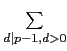 n(d )=
n(d )= 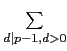
![]() (d ),
可得對所有的
d
(d ),
可得對所有的
d ![]()
![]() 滿足 d| p - 1 皆有
n(d )=
滿足 d| p - 1 皆有
n(d )= ![]() (d ).
(d ).
特別地
n(p - 1) = ![]() (p - 1) 表示在 modulo p 之下有
(p - 1) 表示在 modulo p 之下有
![]() (p - 1)
(p - 1)![]() 0
個元素其 order 為 p - 1, 也就是說這些元素皆為 primitive root. 故知在
modulo p 之下 primitive root 是存在的.
0
個元素其 order 為 p - 1, 也就是說這些元素皆為 primitive root. 故知在
modulo p 之下 primitive root 是存在的.
![]()
我們證明了在 modulo p 之下 primitive root 是存在的. 這個證明方式很明顯的並沒有告訴我們如何找到 primitive root. 事實上我們所用的證明方式有點像反證法, 也就是說如果沒有 primitive root, 那麼在計算上面那些元素個數時會發生數目兜不攏的情形而造成矛盾.