

下一頁: Convolution
上一頁: Arithmetic Function
前一頁: 正因數個數及正因數和
我們要探討比 n 小且與 n
互質的正整數個數.
Definition 2.3.1
給定
n 

,

(
n) 表示比
n 小且與
n 互質的正整數個數.
這樣定出的函數

:

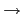

, 稱之為 Euler

-function.
我們要證明 Euler  -function 是 multiplicative,
並求其在任意正整數之取值. 由於不容易找到簡單的 multiplicative
arithmetic function f 使得
-function 是 multiplicative,
並求其在任意正整數之取值. 由於不容易找到簡單的 multiplicative
arithmetic function f 使得  表示成如 Theorem 2.1.5
的形式, 所以我們要直接證明
表示成如 Theorem 2.1.5
的形式, 所以我們要直接證明  是 multiplicative. 也就是說對任意
a, b
是 multiplicative. 也就是說對任意
a, b 
 滿足
gcd(a, b) = 1, 我們要證明
滿足
gcd(a, b) = 1, 我們要證明
 (ab) =
(ab) =  (a)
(a) (b).
(b).
首先我們看一個 a = 5, b = 4 的例子. 我們要說明
 (20) =
(20) =  (5)
(5) (4). 由於
(4). 由於  (20) 表示比 20 小且與 20
互質的正整數個數, 所以我們將小於等於 20 的正整數如下列出:
(20) 表示比 20 小且與 20
互質的正整數個數, 所以我們將小於等於 20 的正整數如下列出:
| 1 |
6 |
11 |
16 |
| 2 |
7 |
12 |
17 |
| 3 |
8 |
13 |
18 |
| 4 |
9 |
14 |
19 |
| 5 |
10 |
15 |
20 |
很容易看出最後一列
5 10 15 20
中每一個數都是 5 的倍數所以不可能和 20 互質,
因此我們要刪除這一列. 而其餘 4 列每一列中的數除以 5
的餘數都相同且都不等於 0 所以這 4 列的數都和 5 互質.
因此我們只要考慮這 4 列的數哪些和 4 是互質的.
仔細觀察這每一列中的數除以 4 的餘數都相異因此每列中只有餘 1 和餘 3
的兩個數和 4 互質. 總結來說我們發現共有  (5) = 4 列的數和 5
互質, 而這 4 列的數中每列皆有
(5) = 4 列的數和 5
互質, 而這 4 列的數中每列皆有  (4) = 2 個數和 4 互質, 因此 1
到 20 之中共有
(4) = 2 個數和 4 互質, 因此 1
到 20 之中共有
 (5)
(5) (4) = 8 個數和 5 且和 4 互質.
這些數就是 1 到 20 之中和 20 互質的數, 所以知
(4) = 8 個數和 5 且和 4 互質.
這些數就是 1 到 20 之中和 20 互質的數, 所以知
 (20) =
(20) =  (5)
(5) (4).
(4).
接下來我們就是要用前面的方法證明一般的情形.
要注意前面的方法我們並無真正點出哪些數和 20 互質,
因為我們只想知道個數再加上我們的方法幾乎和 a = 5, b = 4
無關所以比實際找出哪些數和 20 互質更能運用在一般的狀況.
首先我們用到和 20 互質的數就是和 5 且和 4 互質的數,
這個性質在一般的情況都對.
Lemma 2.3.2
假設
a,
b,
c 
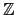
. 則
gcd(
ab,
c) = 1 若且唯若
gcd(
a,
c) = 1 且
gcd(
b,
c) = 1.
証 明.
假設
gcd(
ab,
c) = 1. 若
d = gcd(
a,
c), 表示
d 是
a,
c 的公因數,
所以
d 也是
ab 和
c 的公因數, 故得
d = 1. 同理知
gcd(
b,
c) = 1.
反之, 假設
gcd(a, c) = 1 且
gcd(b, c) = 1. 若
gcd(ab, c)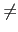 1,
表示存在一質數 p 滿足
p| gcd(ab, c). 也就是說 p| ab 且 p| c. 但
p 是質數, 故由 Lemma 1.4.2 知 p| a 或 p| b. 得知 p 是
a, c 或 b, c 的公因數. 此和
gcd(a, c) = 1 且
gcd(b, c) = 1 相矛盾,
故知
gcd(ab, c) = 1.
1,
表示存在一質數 p 滿足
p| gcd(ab, c). 也就是說 p| ab 且 p| c. 但
p 是質數, 故由 Lemma 1.4.2 知 p| a 或 p| b. 得知 p 是
a, c 或 b, c 的公因數. 此和
gcd(a, c) = 1 且
gcd(b, c) = 1 相矛盾,
故知
gcd(ab, c) = 1.
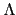
在前面求與 20 互質的數中, 另一個重要步驟是任一排中每一個數除以 4
的餘數都相異, 這在一般
gcd(a, b) = 1 的情況都是對的.
Lemma 2.3.3
假設
a,
b,
l 
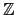
,
b > 1 且
gcd(
a,
b) = 1. 則在
l,
l +
a,
l + 2
a,...,
l + (
b - 1)
a, 中每一個數除以
b 的餘數皆相異.
而且其中共有

(
b) 個元素和
b 互質.
証 明.
若
u,
v 
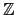
且
u,
v 除以
b 的餘數相同, 表示
b|
u -
v. 因此要說
l,
l +
a,...,
l + (
b - 1)
a 中的元素除以
b 的餘數皆相異, 就是說任取
l +
ia,
l +
ja, 其中
0
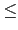 i
i <
j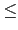 b
b - 1, 都無法使得
b 整除
(
l +
ja) - (
l +
ia). 今假設
b|(
l +
ja) - (
l +
ia), 也就是說
b|(
j -
i)
a. 由於
gcd(
a,
b) = 1, Proposition
1.2.7(1) 告訴我們
b|
j -
i. 但此與
0
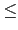 i
i <
j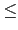 b
b - 1 相矛盾, 故由反證法知
b 不整除
(
l +
ja) - (
l +
ia).
也就是說任取
l +
ia,
l +
ja, 其中
0
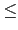 i
i <
j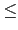 b
b - 1, 則它們除以
b
之餘數皆相異.
對於
i  {0, 1,..., b - 1} 若令 ri 表示 l + ia 除以 b 的餘數,
由於
0
{0, 1,..., b - 1} 若令 ri 表示 l + ia 除以 b 的餘數,
由於
0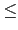 ri
ri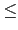 b - 1 且這 b 個 ri 皆相異, 我們知
{r0, r1,..., rb - 1} 這一個集合和
{0, 1,..., b - 1}
是相同的. 然而 Lemma 1.3.1 告訴我們
gcd(l + ia, b) = gcd(ri, b), 所以
{l, l + a,..., l + (b - 1)a} 中和 b
互質的數和
{0, 1,..., b - 1} 中和 b 互質的數之個數相同. 依定義知
{0, 1,..., b - 1} 中共有
b - 1 且這 b 個 ri 皆相異, 我們知
{r0, r1,..., rb - 1} 這一個集合和
{0, 1,..., b - 1}
是相同的. 然而 Lemma 1.3.1 告訴我們
gcd(l + ia, b) = gcd(ri, b), 所以
{l, l + a,..., l + (b - 1)a} 中和 b
互質的數和
{0, 1,..., b - 1} 中和 b 互質的數之個數相同. 依定義知
{0, 1,..., b - 1} 中共有  (b) 個數與 b 互質, 故得證.
(b) 個數與 b 互質, 故得證.
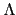
接下來我們證明  是一個 multiplicative arithmetic function.
是一個 multiplicative arithmetic function.
証 明.
我們將小於
ab 的正整數依下列方法排成
b 列:
| 1 |
1 + a |
... |
1 + (b - 1)a |
| 2 |
2 + a |
... |
2 + (b - 1)a |
 |
 |
 |
 |
| a |
2a |
... |
ba |
其中第
l 列為
l,
l +
a,...,
l + (
b - 1)
a. 由
Lemma
1.3.1 知這裡每一數和
a 的最大公因數皆與
l 和
a
的最大公因數相同. 換言之, 若
l 和
a 互質則第
l 列中每一數皆和
a 互質; 而若
l 和
a 不互質則第
l 列中每一數皆和
a 不互質.
又因為
1
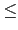 l
l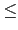 a
a, 故依定義共有

(
a) 個
l 會與
a 互質.
而我們就僅考慮這

(
a) 列的數 (其餘的數都和
a 不互質故和
ab
不互質).
這  (a) 列的數雖都和 a 互質但並不都和 b 互質.
然而每一列皆為
l, l + a,..., l + (b - 1)a 的形式, 故由
gcd(a, b) = 1
以及 Lemma 2.3.3 知每一列皆有
(a) 列的數雖都和 a 互質但並不都和 b 互質.
然而每一列皆為
l, l + a,..., l + (b - 1)a 的形式, 故由
gcd(a, b) = 1
以及 Lemma 2.3.3 知每一列皆有  (b) 個數和 b 互質. 故
1 到 ab 中總共有
(b) 個數和 b 互質. 故
1 到 ab 中總共有
 (a)
(a) (b) 個元素和 a 且和 b 互質. 由
Lemma 2.3.2 這些數就是和 ab 互質的數. 故得證
(b) 個元素和 a 且和 b 互質. 由
Lemma 2.3.2 這些數就是和 ab 互質的數. 故得證
 (ab) =
(ab) =  (a)
(a) (b).
(b).
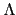
既然  是 multiplicative, 我們就可以利用 Proposition 2.1.3
算出
是 multiplicative, 我們就可以利用 Proposition 2.1.3
算出  之值.
之值.
Proposition 2.3.5
若
n =
p1n1 ... prnr, 其中
pi 為相異質數, 則
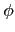
(
n) = (
p1n1 -
p1n1 - 1)
... (
prnr -
prnr - 1) =
n(1 -

)
... (1 -

).
証 明.
我們先求對任意質數
p 以及正整數
t,

(
pt) 之值. 由於
p 是
pt 唯一的質因數,
u 和
pt 不互質表示
p 必為
u
之因數. 因此要計算小於
pt 的正整數中有多少與
pt 互質,
只要算出這些數中有哪些是
p 的倍數再扣掉即可. 然而 1 到
pt
中共有
pt/
p 個數是
p 的倍數. 故得知 1 到
pn 中共有
pt -
pt - 1 個整數和
pt 互質.
現考慮任意
n 
 . 若 n = 1, 我們知
. 若 n = 1, 我們知
 (n) =
(n) =  (1) = 1; 而若
n = p1n1 ... prnr 其中 pi 為相異質數, 則由
(1) = 1; 而若
n = p1n1 ... prnr 其中 pi 為相異質數, 則由  是
multiplicative 知
是
multiplicative 知
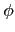
(
n) =
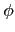
(
p1n1)
... 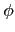
(
prnr) = (
p1n1 -
p1n1 - 1)
... (
prnr -
prnr - 1) =
n(1 -

)
... (1 -

).
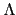
既然  是 multiplicative, 我們可以利用 Theorem 2.1.5
造出另一個 multiplicative arithmetic function. 考慮
F :
是 multiplicative, 我們可以利用 Theorem 2.1.5
造出另一個 multiplicative arithmetic function. 考慮
F : 
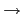
 其定義為對任意
n
其定義為對任意
n 
 ,
F(n) =
,
F(n) = 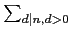
 (d ). 由於 F 是
multiplicative, 且對任意質數 p 以及
t
(d ). 由於 F 是
multiplicative, 且對任意質數 p 以及
t 
 , 我們有
, 我們有
F(
pt) =
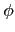
(1) +
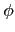
(
p) +
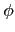
(
p2) +
... +
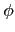
(
pt) = 1 + (
p - 1) + (
p2 -
p) +
... + (
pt -
pt - 1) =
pt.
因此我們有以下之結果.
証 明.
令
F(
n) =
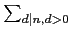

(
d ), 由前知
F 不是 0 函數故由
F 是
multiplicative, 利用 proposition
2.1.3 知
F(1) = 1. 若
n 

且
n > 1 時, 將
n 寫成
n =
p1n1 ... prnr, 其中
pi
為相異質數, 再由上面
F(
pt) =
pt 的結果及 Proposition
2.1.3 知
F(n) = F(p1n1) ... F(prnr) = p1n1 ... prnr = n,
得證本定理.


下一頁: Convolution
上一頁: Arithmetic Function
前一頁: 正因數個數及正因數和
Li
2007-06-28
![]() -function 是 multiplicative,
並求其在任意正整數之取值. 由於不容易找到簡單的 multiplicative
arithmetic function f 使得
-function 是 multiplicative,
並求其在任意正整數之取值. 由於不容易找到簡單的 multiplicative
arithmetic function f 使得 ![]() 表示成如 Theorem 2.1.5
的形式, 所以我們要直接證明
表示成如 Theorem 2.1.5
的形式, 所以我們要直接證明 ![]() 是 multiplicative. 也就是說對任意
a, b
是 multiplicative. 也就是說對任意
a, b ![]()
![]() 滿足
gcd(a, b) = 1, 我們要證明
滿足
gcd(a, b) = 1, 我們要證明
![]() (ab) =
(ab) = ![]() (a)
(a)![]() (b).
(b).
![]() (20) =
(20) = ![]() (5)
(5)![]() (4). 由於
(4). 由於 ![]() (20) 表示比 20 小且與 20
互質的正整數個數, 所以我們將小於等於 20 的正整數如下列出:
(20) 表示比 20 小且與 20
互質的正整數個數, 所以我們將小於等於 20 的正整數如下列出:
![]() 1,
表示存在一質數 p 滿足
p| gcd(ab, c). 也就是說 p| ab 且 p| c. 但
p 是質數, 故由 Lemma 1.4.2 知 p| a 或 p| b. 得知 p 是
a, c 或 b, c 的公因數. 此和
gcd(a, c) = 1 且
gcd(b, c) = 1 相矛盾,
故知
gcd(ab, c) = 1.
1,
表示存在一質數 p 滿足
p| gcd(ab, c). 也就是說 p| ab 且 p| c. 但
p 是質數, 故由 Lemma 1.4.2 知 p| a 或 p| b. 得知 p 是
a, c 或 b, c 的公因數. 此和
gcd(a, c) = 1 且
gcd(b, c) = 1 相矛盾,
故知
gcd(ab, c) = 1.
![]()
![]() {0, 1,..., b - 1} 若令 ri 表示 l + ia 除以 b 的餘數,
由於
0
{0, 1,..., b - 1} 若令 ri 表示 l + ia 除以 b 的餘數,
由於
0![]() ri
ri![]() b - 1 且這 b 個 ri 皆相異, 我們知
{r0, r1,..., rb - 1} 這一個集合和
{0, 1,..., b - 1}
是相同的. 然而 Lemma 1.3.1 告訴我們
gcd(l + ia, b) = gcd(ri, b), 所以
{l, l + a,..., l + (b - 1)a} 中和 b
互質的數和
{0, 1,..., b - 1} 中和 b 互質的數之個數相同. 依定義知
{0, 1,..., b - 1} 中共有
b - 1 且這 b 個 ri 皆相異, 我們知
{r0, r1,..., rb - 1} 這一個集合和
{0, 1,..., b - 1}
是相同的. 然而 Lemma 1.3.1 告訴我們
gcd(l + ia, b) = gcd(ri, b), 所以
{l, l + a,..., l + (b - 1)a} 中和 b
互質的數和
{0, 1,..., b - 1} 中和 b 互質的數之個數相同. 依定義知
{0, 1,..., b - 1} 中共有 ![]() (b) 個數與 b 互質, 故得證.
(b) 個數與 b 互質, 故得證.
![]()
![]() 是一個 multiplicative arithmetic function.
是一個 multiplicative arithmetic function.
![]() (a) 列的數雖都和 a 互質但並不都和 b 互質.
然而每一列皆為
l, l + a,..., l + (b - 1)a 的形式, 故由
gcd(a, b) = 1
以及 Lemma 2.3.3 知每一列皆有
(a) 列的數雖都和 a 互質但並不都和 b 互質.
然而每一列皆為
l, l + a,..., l + (b - 1)a 的形式, 故由
gcd(a, b) = 1
以及 Lemma 2.3.3 知每一列皆有 ![]() (b) 個數和 b 互質. 故
1 到 ab 中總共有
(b) 個數和 b 互質. 故
1 到 ab 中總共有
![]() (a)
(a)![]() (b) 個元素和 a 且和 b 互質. 由
Lemma 2.3.2 這些數就是和 ab 互質的數. 故得證
(b) 個元素和 a 且和 b 互質. 由
Lemma 2.3.2 這些數就是和 ab 互質的數. 故得證
![]() (ab) =
(ab) = ![]() (a)
(a)![]() (b).
(b).
![]()
![]() 是 multiplicative, 我們就可以利用 Proposition 2.1.3
算出
是 multiplicative, 我們就可以利用 Proposition 2.1.3
算出 ![]() 之值.
之值.
![]()
![]() . 若 n = 1, 我們知
. 若 n = 1, 我們知
![]() (n) =
(n) = ![]() (1) = 1; 而若
n = p1n1 ... prnr 其中 pi 為相異質數, 則由
(1) = 1; 而若
n = p1n1 ... prnr 其中 pi 為相異質數, 則由 ![]() 是
multiplicative 知
是
multiplicative 知
![]() 是 multiplicative, 我們可以利用 Theorem 2.1.5
造出另一個 multiplicative arithmetic function. 考慮
F :
是 multiplicative, 我們可以利用 Theorem 2.1.5
造出另一個 multiplicative arithmetic function. 考慮
F : ![]()
![]()
![]() 其定義為對任意
n
其定義為對任意
n ![]()
![]() ,
F(n) =
,
F(n) = ![]()
![]() (d ). 由於 F 是
multiplicative, 且對任意質數 p 以及
t
(d ). 由於 F 是
multiplicative, 且對任意質數 p 以及
t ![]()
![]() , 我們有
, 我們有