

下一頁: 算數基本定理
上一頁: 整數的基本性質
前一頁: 輾轉相除法
這一節我們要談整數的分解中最基本的元素: 質數. 大家都知道一個質數 p
就是正因數只有 1 和本身的數. 我們仍給一個正式的定義.
Definition 1.4.1
若
p 

,
p > 1 且
p 的正公因數只有
p 和 1 則稱
p
是一個質數 (prime number). 若一正整數有其他的正因數則稱為合成數
(composite number).
簡單來說質數就是無法分解成兩個較小的正整數乘積的數.
質數這一種不可分解的特性讓它有很多特殊性質. 例如給定一質數 p
以及一整數
a 
 , 我們很容易判定 gcd(a, p) 為何. 若
d = gcd(a, p) 則因 d| p, 知 d = 1 或 d = p. 若 d = p 表示 p| a,
所以我們知由 p
, 我們很容易判定 gcd(a, p) 為何. 若
d = gcd(a, p) 則因 d| p, 知 d = 1 或 d = p. 若 d = p 表示 p| a,
所以我們知由 p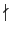 a, 可得 d = 1. 所以利用 Proposition
1.2.7(1) 我們有以下之結論.
a, 可得 d = 1. 所以利用 Proposition
1.2.7(1) 我們有以下之結論.
Lemma 1.4.2 (Euclid)
假設
p 是一個質數, 且
a,
b 

. 若
p|
ab, 則
p|
a 或
p|
b.
証 明.
這裡我們要證明
p|
a 或
p|
b. 如果
p|
a 當然就可以了 (不必擔心是否
p|
b); 但若
p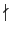 a
a, 那麼我們就得證明
p|
b. 不過由前知
p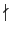 a
a 表示
gcd(
p,
a) = 1, 故利用 Proposition
1.2.7(1) 得證
p|
b.

Euclid 這一個 Lemma 告訴我們一個質數若是 ab 的因數那它一定是 a, b
其中之ㄧ的因數. 事實上這個性質並不只適用在兩個整數相乘的情況,
我們很容易推廣至更多數相乘之情況.
Corollary 1.4.3
假設
p 是一個質數, 且
a1,
a2,...,
an 

. 若
p|
a1a2 ... an, 則存在
i 
{1,...,
n} 滿足
p|
ai.
証 明.
我們依然用數學歸納法證明. 當
k = 2 時由 Lemma
1.4.2 知若
p|
a1a2, 則
p|
a1 或
p|
a2. 假設
k =
n - 1 時成立, 即若有
n - 1
個整數
a1,...,
an - 1 滿足
p|
a1 ... an - 1, 則存在
i 
{1,...,
n - 1} 使得
p|
ai. 現考慮
k =
n 的情形, 若
a1,...,
an 是
n 個整數滿足
p|
a1 ... an, 則令
a =
a1 ... an - 1,
b =
an. 此時由
p|
ab 及 Lemma
1.4.2
知
p|
a 或
p|
b. 若
p|
a, 則由數學歸納法假設知存在
i 
{1,...,
n - 1} 使得
p|
ai, 而若
p|
b 即
p|
an,
故得證本定理.

若一質數 p 是一整數 a 的因數, 則我們稱 p 是 a 的一個質因數.
當然了質數 p 本身就是 p 的質因數, 而一個合成數會不會有質因數呢?
大家很自然的覺得一定有, 我們還是給一個正式的證明.
証 明.
我們用數學歸納法. 首先若
a = 2, 則由於 2 是質數我們得
p = 2
為所求. 現假設對任意
b 

滿足
2
 b
b n
n 的數皆存在質數
p
使得
p|
b, 我們考慮
a =
n + 1 的情形. 若
a 本身是質數那當然
p =
a
為所求. 反之, 如果
a 不是質數依定義存在
b 

且 2
 b
b <
a
使得
b|
a. 故由數學歸納法假設知存在一質數
p 滿足
p|
b. 因此利用
Proposition
1.1.3(2) 得證
p|
a.

雖然正整數有無窮多個而 Lemma 1.4.4 告訴我們每一個大於 1
的正整數都有質因數, 但這並不代表會有無窮多個質數.
接著我們就是要探討質數確有無窮多個.
一般來說要證明質數有無窮多個或許會有的想法是希望利用現有的質數創造更大的質數.
不過這個想法是不可行的,
主要的原因是到目前為止我們沒有一個判別一個數是否為質數好的方法.
另類的思考是用反證法, 假設只有有限個質數而得到矛盾.
這個方法就不會碰到判別質數的問題,
相信由此大家更能體會到反證法的妙用.
証 明.
我們用反證法假設只有有限個質數. 既然只有有限個我們可以將之ㄧ一列出,
就假設
p1,...,
pn 是所有的質數. 現考慮
a =
p1 ... pn + 1, 由
Lemma
1.4.4 知必有一質數
pi,
i 
{1,...,
n} 滿足
pi|
a. 然而
pi 本身整除
p1 ... pn 故由 Corollary
1.1.2 知
pi|
a -
p1 ... pn, 也就是說
pi| 1 而得到矛盾.
故知不可能僅有有限多個質數, 而得證有無窮多個質數.

質數雖然有無窮多個不過他們的分布不是非常稠密的. 例如給定任意大的整數
n 我們可以找到 n 個連續整數都不是質數. 我們的找法是考慮
(n + 1)! + 2,(n + 1)! + 3,...,(n + 1)! + n + 1
這 n 個連續整數.
很容意看出它們都不是質數.
就是質數這麼不容易出現加上很難判別一個很大的數是否為質數,
所以質數常被應用在密碼學中. 底下我們介紹一種最簡單判斷質數的方法.
証 明.
因為我們無法直接證明
n 會是質數, 所以需用反證法. 假設
n
不是質數, 依定義知存在
a,
b 

滿足
1 <
a b
b <
n 且
n =
ab.
由此我們可以確定
a
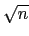
, 否則若
a >
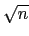
會造成
ab > (
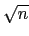
)
2 =
n 而與
n =
ab 不合. 而由 Lemma
1.4.4
知存在質數
p 使得
p|
a. 既然
p|
a 我們得
p a
a
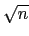
且
p|
n. 此與假設所有小於等於
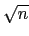
的質數皆不整除
n 不符, 故知
n 為質數.

Proposition 1.4.6 所提判別質數方法稱為篩法 (sieve method).
它可以幫助我們篩得哪些數是質數. 例如若要找出所有小於 100 的質數.
我們只要將小於
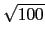 = 10 的質數 (即 2, 3, 5, 7) 找出, 留下
2, 3, 5, 7 然後將其餘 2, 3, 5, 7 的倍數刪除, 經過這樣篩選後留下來小於
100 的數就都是小於 100 的質數. 這是因為若 n < 100 且不是質數, 則由
Proposition 1.4.6 知 n 必有一質因數小於等於
= 10 的質數 (即 2, 3, 5, 7) 找出, 留下
2, 3, 5, 7 然後將其餘 2, 3, 5, 7 的倍數刪除, 經過這樣篩選後留下來小於
100 的數就都是小於 100 的質數. 這是因為若 n < 100 且不是質數, 則由
Proposition 1.4.6 知 n 必有一質因數小於等於
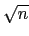 <
< 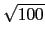 = 10. 因此被我們所刪除 2, 3, 5, 7
的倍數就是所有小於 100 的合成數, 自然剩下的便都是質數了.
= 10. 因此被我們所刪除 2, 3, 5, 7
的倍數就是所有小於 100 的合成數, 自然剩下的便都是質數了.
質數既然有無窮多個,
接下來我們可以問是否有些特定形式的質數也會有無窮多個?
例如我們知道偶數中只有 2 是質數, 因此可以將所有奇數分類, 分成
4n + 1 和 4n + 3 這兩類然後問哪一類會有無窮多個質數. 要注意 4n + 1
這一類的數有一重要特性就是兩個 4n + 1 形式的數相乘仍然是 4n + 1
的形式. 因此任意有限多個 4n + 1 形式的數相乘仍是 4n + 1 的形式,
也就是說這一類的數有乘法封閉性. 另一方面 4n + 3
的形式的數就沒有這個特性, 事實上兩個 4n + 3
形式的數相乘會變成 4n + 1 的形式. 利用這兩類數的特性以及類似 Lemma
1.4.4 的證明, 我們有以下之結果.
Lemma 1.4.7
假設
a = 4
n + 3 其中
n 

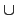
{0}, 則必存在一質數
p = 4
n' + 3 其中
n' 

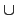
{0} 滿足
p|
a.
証 明.
我們利用數學歸納法證明. 首先若
a = 3, 則由於 3 是質數我們得
p = 3
為所求. 現假設對任意
b = 4
k + 3


滿足
0
 k
k n
n - 1
的數皆存在質數
p = 4
k' + 3 使得
p|
b, 我們考慮
k =
n 的情形. 若
a
本身是質數那當然
p =
a 為所求. 反之, 如果
a 不是質數依定義存在
b,
c 

其中
b <
a 且
c <
a 使得
a =
bc. 注意
b,
c
中必有一個元素是 4
k + 3 形式, 否則
b,
c 都是 4
k + 1 形式會造成
bc =
a 也是 4
k + 1 形式的矛盾現象. 就假設
b = 4
k + 3 吧! 此時
0
 k
k n
n - 1 (因
b <
a), 故由歸納假設知存在
p = 4
k' + 3 使得
p|
b,
因而得證
p|
a.

注意 4n + 1 形式的數並不一定有 4n + 1 形式的質因數. 9
就是最簡的的例子. 觀察由 Lemma 1.4.4 推得 Theorem 1.4.5
的關係, 同樣的我們也可利用 Lemma 1.4.7 推得 4n + 3
形式的質數有無窮多個.
証 明.
我們依然用反證法假設
S 中只有有限多個質數並令
p0 = 3,
p1,...,
pn 是
S 中所有的相異質數. 現考慮
a = 4(
p1 ... pn) + 3. 由於
a  S
S 利用 Lemma
1.4.7 知必有一質數
p  S
S
滿足
p|
a, 故由假設知存在
i 
{0,...,
n} 使得
p =
pi, .
若 p = p0 = 3, 則由 3| a, 3| 3 以及
a - 3 = 4(p1 ... pn) 得知
3| 4(p1 ... pn), 故由 Corollary 1.4.3 得到 3| 4 或者
3| pi,
i  {1,..., n} 這樣的矛盾.
{1,..., n} 這樣的矛盾.
若 p = pi 其中
i  {1,..., n}, 則由 pi 本身整除
p1 ... pn 知
pi| a - 4(p1 ... pn), 也就是說 pi| 3 而得到矛盾.
故得證 S 中不可能僅有有限多個質數.
{1,..., n}, 則由 pi 本身整除
p1 ... pn 知
pi| a - 4(p1 ... pn), 也就是說 pi| 3 而得到矛盾.
故得證 S 中不可能僅有有限多個質數.

因為 Lemma 1.4.7 並不適用於 4n + 1 形式的整數, 所以
Proposition 1.4.8 的方法不能用來討論 4n + 1 形式的質數, 不過
4n + 1 形式的質數仍有無窮多個. 事實上數論一個很重要的定理 (Dirichlet
Theorem) 告訴我們對任意互質的兩整數 a, b 皆有無窮多個 an + b
形式的質數. 這個定理的證明超出本講義範圍, 我們就不再多談了.


下一頁: 算數基本定理
上一頁: 整數的基本性質
前一頁: 輾轉相除法
Li
2007-06-28
![]()
![]() , 我們很容易判定 gcd(a, p) 為何. 若
d = gcd(a, p) 則因 d| p, 知 d = 1 或 d = p. 若 d = p 表示 p| a,
所以我們知由 p
, 我們很容易判定 gcd(a, p) 為何. 若
d = gcd(a, p) 則因 d| p, 知 d = 1 或 d = p. 若 d = p 表示 p| a,
所以我們知由 p![]() a, 可得 d = 1. 所以利用 Proposition
1.2.7(1) 我們有以下之結論.
a, 可得 d = 1. 所以利用 Proposition
1.2.7(1) 我們有以下之結論.
![]() = 10 的質數 (即 2, 3, 5, 7) 找出, 留下
2, 3, 5, 7 然後將其餘 2, 3, 5, 7 的倍數刪除, 經過這樣篩選後留下來小於
100 的數就都是小於 100 的質數. 這是因為若 n < 100 且不是質數, 則由
Proposition 1.4.6 知 n 必有一質因數小於等於
= 10 的質數 (即 2, 3, 5, 7) 找出, 留下
2, 3, 5, 7 然後將其餘 2, 3, 5, 7 的倍數刪除, 經過這樣篩選後留下來小於
100 的數就都是小於 100 的質數. 這是因為若 n < 100 且不是質數, 則由
Proposition 1.4.6 知 n 必有一質因數小於等於
![]() <
< ![]() = 10. 因此被我們所刪除 2, 3, 5, 7
的倍數就是所有小於 100 的合成數, 自然剩下的便都是質數了.
= 10. 因此被我們所刪除 2, 3, 5, 7
的倍數就是所有小於 100 的合成數, 自然剩下的便都是質數了.
![]() {1,..., n} 這樣的矛盾.
{1,..., n} 這樣的矛盾.
![]() {1,..., n}, 則由 pi 本身整除
p1 ... pn 知
pi| a - 4(p1 ... pn), 也就是說 pi| 3 而得到矛盾.
故得證 S 中不可能僅有有限多個質數.
{1,..., n}, 則由 pi 本身整除
p1 ... pn 知
pi| a - 4(p1 ... pn), 也就是說 pi| 3 而得到矛盾.
故得證 S 中不可能僅有有限多個質數.
![]()