

: The Euler -function
: Arithmetic Function
玡: Multiplicative Arithmetic Functions
иノ multiplicative arithmetic function
阀├е―タ俱计ㄤタ计ぇ计のタ计㎝.
倒﹚タ俱计 n, v(n) ボ n タ计计. 琂礛癸ヴ種
n 
 , v(n) 常Τ, ┮и盢ㄤΘ琌ㄧ计
v :
, v(n) 常Τ, ┮и盢ㄤΘ琌ㄧ计
v : 
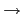
 . 眖ㄧ计àㄓ, v 碞琌 arithmetic function.
倒﹚
n
. 眖ㄧ计àㄓ, v 碞琌 arithmetic function.
倒﹚
n 
 ― v(n) ㎡? 钡猭碞琌盢 n
タ计礛计Τぶ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
v(6) = 4. 硂妓―猭ノΑボ㎡? и到ノ summation
― v(n) ㎡? 钡猭碞琌盢 n
タ计礛计Τぶ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
v(6) = 4. 硂妓―猭ノΑボ㎡? и到ノ summation  才腹, 盢 v(n) 糶Θ
才腹, 盢 v(n) 糶Θ
v(
n) =

1.
Α種碞琌–Ω d 骸ì d| n d > 0 碞Ω,
┮礛眔 n タ计计.
Proposition 2.2.1
癸ヴ種
n 

,
v(
n) ボ
n タ计计. 玥
v :

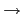

琌 multiplicative arithmetic function. τ璝
n =
p1n1 ... prnr, ㄤい
pi 钵借计, 玥
v(
n) = (
n1 + 1)
... (
nr + 1).
谍 .
璝
l :

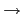

琌 arithmetic function 骸ì癸ヴ種
n 

,
l(
n) = 1, 玥
v(
n)
v(
n) =
 l
l(
d ).
パ癸ヴ種
a,
b 

,
l(
ab) =
l(
a)
l(
b) = 1, и
l (completely)
multiplicative. パ Theorem
2.1.5
v multiplicative.
琂礛 v 琌 multiplicative, иノ Proposition 2.1.3
―癸ヴ種
n 
 , v(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t, v(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i
, v(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t, v(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i  {0, 1,..., t}, и眔
v(pt) = t + 1. 癸ヴ種
n
{0, 1,..., t}, и眔
v(pt) = t + 1. 癸ヴ種
n 
 ,
璝 n = 1, и
v(n) = v(1) = 1; τ璝
n = p1n1 ... prnr
ㄤい pi 钵借计, 玥パ v 琌 multiplicative
,
璝 n = 1, и
v(n) = v(1) = 1; τ璝
n = p1n1 ... prnr
ㄤい pi 钵借计, 玥パ v 琌 multiplicative
v(n) = v(p1n1) ... v(prnr) = (n1 + 1) ... (nr + 1).
羭ㄒㄓ弧, и璶― 360 タ计计, パ
360 = 23 . 32 . 5,
ノ Proposition 2.2.1, ие碞眔
v(360) = (3 + 1)(2 + 1)(1 + 1) = 24. 眖硂柑產莱砰穦 multiplicative
arithmetic function 矪. ┪砛― v(n)
そΑ產蔼い厩逼舱碞ノ猭瞶眔筁.
ノ猭瞶ㄤ龟碞㎝ v 琌 multiplicative 闽.
钡ㄓи贝癚タ计㎝. 倒﹚タ俱计 n, 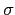 (n) ボ n
┮Τタ计ぇ㎝. 琂礛癸ヴ種
n
(n) ボ n
┮Τタ计ぇ㎝. 琂礛癸ヴ種
n 
 ,
, 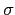 (n) 常Τ,
┮и盢ㄤΘ琌ㄧ计
(n) 常Τ,
┮и盢ㄤΘ琌ㄧ计
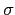 :
: 
 . 眖ㄧ计àㄓ,
. 眖ㄧ计àㄓ,
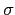 碞琌 arithmetic function. 倒﹚
n
碞琌 arithmetic function. 倒﹚
n 
 ―
―
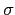 (n) ㎡? 钡猭碞琌盢 n
タ计礛场癬ㄓ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
(n) ㎡? 钡猭碞琌盢 n
タ计礛场癬ㄓ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
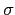 (6) = 1 + 2 + 3 + 6 = 12. 硂妓―猭ノΑボ㎡? иΩ到ノ
summation
(6) = 1 + 2 + 3 + 6 = 12. 硂妓―猭ノΑボ㎡? иΩ到ノ
summation  才腹, 盢
才腹, 盢 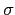 (n) 糶Θ
(n) 糶Θ
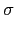
(
n) =
 d
d.
Α種碞琌–Ω d 骸ì d| n
d > 0 碞 d, ┮礛眔 n タ计㎝.
Proposition 2.2.2
癸ヴ種
n 

,
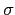
(
n) ボ
n タ计计. 玥
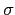
:

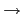

琌 multiplicative arithmetic function. τ璝
n =
p1n1 ... prnr, ㄤい
pi 钵借计, 玥
谍 .
璝
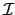
:

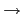

琌 arithmetic function 骸ì癸ヴ種
n 

,
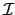
(
n) =
n, 玥
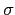
(
n)
パ癸ヴ種
a,
b 

,
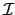
(
ab) =
ab =
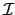
(
a)
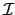
(
b), и
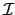
(completely)
multiplicative. パ Theorem
2.1.5
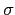
multiplicative.
琂礛 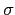 琌 multiplicative, иノ Proposition 2.1.3
―癸ヴ種
n
琌 multiplicative, иノ Proposition 2.1.3
―癸ヴ種
n 
 ,
, 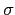 (n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t,
(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t,
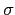 (pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i
(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i  {0, 1,..., t}, и眔
{0, 1,..., t}, и眔
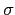 (pt) = 1 + p + ... + pt. パ
1, p,..., pt 琌そゑ p 单ゑ计, и眔
(pt) = 1 + p + ... + pt. パ
1, p,..., pt 琌そゑ p 单ゑ计, и眔
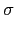
(
pt) =

.
癸ヴ種
n 

, 璝
n = 1, и
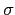
(
n) =
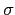
(1) = 1; τ璝
n =
p1n1 ... prnr ㄤい
pi 钵借计, 玥パ
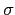
琌 multiplicative
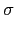
(
n) =
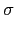
(
p1n1)
... 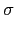
(
prnr) =
 ...
... 
.
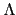
羭ㄒㄓ弧, и璶― 360 タ计㎝, パ
360 = 23 . 32 . 5,
ノ Proposition 2.2.2, ие碞眔
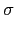
(360) =



= 15
. 13
. 6 = 1170.


: The Euler -function
: Arithmetic Function
玡: Multiplicative Arithmetic Functions
Li
2007-06-28
![]()
![]() , v(n) 常Τ, ┮и盢ㄤΘ琌ㄧ计
v :
, v(n) 常Τ, ┮и盢ㄤΘ琌ㄧ计
v : ![]()
![]()
![]() . 眖ㄧ计àㄓ, v 碞琌 arithmetic function.
倒﹚
n
. 眖ㄧ计àㄓ, v 碞琌 arithmetic function.
倒﹚
n ![]()
![]() ― v(n) ㎡? 钡猭碞琌盢 n
タ计礛计Τぶ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
v(6) = 4. 硂妓―猭ノΑボ㎡? и到ノ summation
― v(n) ㎡? 钡猭碞琌盢 n
タ计礛计Τぶ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
v(6) = 4. 硂妓―猭ノΑボ㎡? и到ノ summation ![]() 才腹, 盢 v(n) 糶Θ
才腹, 盢 v(n) 糶Θ
 1.
1.
 l(d ).
l(d ).
![]()
![]() , v(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t, v(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i
, v(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t, v(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i ![]() {0, 1,..., t}, и眔
v(pt) = t + 1. 癸ヴ種
n
{0, 1,..., t}, и眔
v(pt) = t + 1. 癸ヴ種
n ![]()
![]() ,
璝 n = 1, и
v(n) = v(1) = 1; τ璝
n = p1n1 ... prnr
ㄤい pi 钵借计, 玥パ v 琌 multiplicative
,
璝 n = 1, и
v(n) = v(1) = 1; τ璝
n = p1n1 ... prnr
ㄤい pi 钵借计, 玥パ v 琌 multiplicative
![]() (n) ボ n
┮Τタ计ぇ㎝. 琂礛癸ヴ種
n
(n) ボ n
┮Τタ计ぇ㎝. 琂礛癸ヴ種
n ![]()
![]() ,
, ![]() (n) 常Τ,
┮и盢ㄤΘ琌ㄧ计
(n) 常Τ,
┮и盢ㄤΘ琌ㄧ计
![]() :
: ![]()
![]()
![]() . 眖ㄧ计àㄓ,
. 眖ㄧ计àㄓ,
![]() 碞琌 arithmetic function. 倒﹚
n
碞琌 arithmetic function. 倒﹚
n ![]()
![]() ―
―
![]() (n) ㎡? 钡猭碞琌盢 n
タ计礛场癬ㄓ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
(n) ㎡? 钡猭碞琌盢 n
タ计礛场癬ㄓ. ㄒ 6 タ计Τ 1, 2, 3, 6, ┮
![]() (6) = 1 + 2 + 3 + 6 = 12. 硂妓―猭ノΑボ㎡? иΩ到ノ
summation
(6) = 1 + 2 + 3 + 6 = 12. 硂妓―猭ノΑボ㎡? иΩ到ノ
summation ![]() 才腹, 盢
才腹, 盢 ![]() (n) 糶Θ
(n) 糶Θ
 d.
d.
 ...
...  .
.

![]() 琌 multiplicative, иノ Proposition 2.1.3
―癸ヴ種
n
琌 multiplicative, иノ Proposition 2.1.3
―癸ヴ種
n ![]()
![]() ,
, ![]() (n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t,
(n) ぇ.
碞琌弧и璶贝癚癸ヴ種借计 p のタ俱计 t,
![]() (pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i
(pt)
ぇ. パ pt タ计碞琌 pi, ㄤい
i ![]() {0, 1,..., t}, и眔
{0, 1,..., t}, и眔
![]() (pt) = 1 + p + ... + pt. パ
1, p,..., pt 琌そゑ p 单ゑ计, и眔
(pt) = 1 + p + ... + pt. パ
1, p,..., pt 琌そゑ p 单ゑ计, и眔
 .
.
 ...
...  .
.


 = 15 . 13 . 6 = 1170.
= 15 . 13 . 6 = 1170.