

下一頁: Wilson's Theorem
上一頁: Congruences
前一頁: 同餘的運算
一般在解方程式時, 我們經常需要乘法反元素來幫忙. 所以當
m 
 ,
a
,
a 
 且
gcd(a, m) = 1 時, 若能確實知道哪些
b
且
gcd(a, m) = 1 時, 若能確實知道哪些
b 
 會滿足
ab
會滿足
ab  1(mod m) 將是很有用的. 由 Proposition 3.2.5
的證明中我們知可以利用輾轉相除法解 mx + ay = 1 的整數解來得到 b,
但這要在 m 和 a 皆是具體的數時才能操作. 我們將利用 Euler's
Theorem 對一般的 m, a 都能將 b 確實找到.
1(mod m) 將是很有用的. 由 Proposition 3.2.5
的證明中我們知可以利用輾轉相除法解 mx + ay = 1 的整數解來得到 b,
但這要在 m 和 a 皆是具體的數時才能操作. 我們將利用 Euler's
Theorem 對一般的 m, a 都能將 b 確實找到.
給定
m 
 , 若
a, b
, 若
a, b 
 滿足
ab
滿足
ab  1(mod m), 則由
Proposition 3.2.5 知 a 和 b 皆與 m 互質. 換言之,
我們只要考慮和 m 互質的數即可, 所以我們自然考慮 reduced residue
system modulo m.
1(mod m), 則由
Proposition 3.2.5 知 a 和 b 皆與 m 互質. 換言之,
我們只要考慮和 m 互質的數即可, 所以我們自然考慮 reduced residue
system modulo m.
Lemma 3.3.1
給定
m 

, 考慮
a 

滿足
gcd(
m,
a) = 1. 若
{
r1,...,
r (m)
(m)} 是一個 reduced residue system modulo
m, 則
{
ar1,...,
ar (m)
(m)} 也是一個 reduced residue
system modulo
m.
証 明.
複習一下,
{
r1,...,
r (m)
(m)} 是一個 reduced residue system
modulo
m 表示
gcd(
m,
ri) = 1 且對任意
i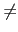 j
j, 皆有
ri  rj
rj(mod
m). 現要證明
{
ar1,...,
ar (m)
(m)}
也是 reduced residue system modulo
m, 我們需要證明
gcd(
m,
ari) = 1 且對任意
i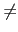 j
j 皆有
ari  arj
arj(mod
m).
現假設
gcd(m, ari)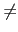 1, 即存在一質數 p 滿足 p| m 且 p| ari.
因 p 是質數, 故由 Lemma 1.4.2 得 p| a 或 p| ri. 換言之,
p 為 m, a 的公因數或是 m, ri 的公因數. 此和
gcd(m, a) = 1 且
gcd(m, ri) = 1 相矛盾, 故得證
gcd(m, ari) = 1.
1, 即存在一質數 p 滿足 p| m 且 p| ari.
因 p 是質數, 故由 Lemma 1.4.2 得 p| a 或 p| ri. 換言之,
p 為 m, a 的公因數或是 m, ri 的公因數. 此和
gcd(m, a) = 1 且
gcd(m, ri) = 1 相矛盾, 故得證
gcd(m, ari) = 1.
另一方面, 若 i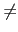 j 且
ari
j 且
ari  arj(mod m), 則由
gcd(m, a) = 1, 利用 Corollary 3.2.4 得
ri
arj(mod m), 則由
gcd(m, a) = 1, 利用 Corollary 3.2.4 得
ri  rj(mod m). 此和
ri
rj(mod m). 此和
ri  rj(mod m) 矛盾, 故得證
ari
rj(mod m) 矛盾, 故得證
ari  arj(mod m).
arj(mod m).

前面提過, 給定
m 
 , 利用除以 m 同餘的分類, 我們可以將與 m
互質的數分成
, 利用除以 m 同餘的分類, 我們可以將與 m
互質的數分成 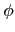 (m) 類.
而將每一類中挑出一代表元素所成之集合就是一個 reduced residue system
modulo m. 今假若
S = {a1,..., a
(m) 類.
而將每一類中挑出一代表元素所成之集合就是一個 reduced residue system
modulo m. 今假若
S = {a1,..., a (m)} 和
T = {b1,..., b
(m)} 和
T = {b1,..., b (m)} 皆為 reduced residue system modulo
m, 任取 ai
(m)} 皆為 reduced residue system modulo
m, 任取 ai  S, 由於它代表與 m 互質的某一同餘類, 而 T
中也有一元素是在和 ai 同類的元素中挑出. 換言之, 存在 bj
S, 由於它代表與 m 互質的某一同餘類, 而 T
中也有一元素是在和 ai 同類的元素中挑出. 換言之, 存在 bj  T
滿足
ai
T
滿足
ai  bj(mod m). 又由於這些 bj 兩兩皆不同類, 所以
S 和 T 中元素在 modulo m 之下有一對一的對應關係.
也就是說經過適當的排序, 我們有
ai
bj(mod m). 又由於這些 bj 兩兩皆不同類, 所以
S 和 T 中元素在 modulo m 之下有一對一的對應關係.
也就是說經過適當的排序, 我們有
ai  bi(mod m). 因此得
a1 ... a
bi(mod m). 因此得
a1 ... a (m)
(m)  b1 ... b
b1 ... b (m)(mod m).
利用這個結果我們可以得證 Euler's Theorem.
(m)(mod m).
利用這個結果我們可以得證 Euler's Theorem.
Theorem 3.3.2 (Euler's Theorem)
給定
m 

, 若
a 

滿足
gcd(
m,
a) = 1, 則
a (m)
(m) 
1(mod
m).
証 明.
取
S = {
r1,....
r (m)
(m)} 為一個 reduced residue system
modulo
m. 首先我們證明
gcd(
m,
r1 ... r (m)
(m)) = 1. 若
gcd(
m,
r1 ... r (m)
(m))
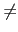
1, 即存在一質數
p 使得
p|
m 且
p|
r1 ... r (m)
(m). 利用 Corollary
1.4.3 知存在
ri  S
S 使得
p|
ri, 也就是說
gcd(
m,
ri)
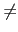
1. 此和
S 是
reduced residue system modulo
m 且
ri  S
S 相矛盾, 故得證
gcd(
m,
r1 ... r (m)
(m)) = 1.
現由於
gcd(m, a) = 1, 故利用 Lemma 3.3.1 知
{ar1,..., ar (m)} 也是一個 reduced residue system modulo
m, 因此得
(m)} 也是一個 reduced residue system modulo
m, 因此得
r1 ... r (m)
(m) 
(
ar1)
... (
ar (m)
(m))
 a
a (m)
(m)(
r1 ... r (m)
(m))(mod
m).
再因為
gcd(
m,
r1 ... r (m)
(m)) = 1, 故利用 Corollary
3.2.4 得證
a (m)
(m) 
1(mod
m).

給定
m 
 及
a
及
a 
 滿足
gcd(m, a) = 1, 若令
b = a
滿足
gcd(m, a) = 1, 若令
b = a (m) - 1, 則利用 Euler's Theorem 得知
ab
(m) - 1, 則利用 Euler's Theorem 得知
ab  a
a (m)
(m)  1(mod m). 因此我們找到了 a 在 modulo m
之下的乘法反元素.
1(mod m). 因此我們找到了 a 在 modulo m
之下的乘法反元素.
Corollary 3.3.3
給定
m 

, 若
a 

滿足
gcd(
m,
a) = 1, 則令
b =
a (m) - 1
(m) - 1, 會滿足
ab  ba
ba 
1(mod
m).
特別地, 當 m 是一個質數 p 時, Euler's Theorem 就是所謂的
Fermat's Little Theorem. 我們特別將它寫下來.
Theorem 3.3.4 (Fermat's Little Theorem)
給定一質數
p, 若
a 

滿足
p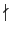 a
a, 則
ap - 1 
1(mod
p).
特別地, 若令
b =
ap - 2, 則
ab  ba
ba 
1(mod
p).
証 明.
因
p 是一質數, 由
p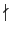 a
a 之假設知
gcd(
p,
a) = 1. 又此時
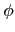
(
p) =
p - 1, 故直接套用 Theorem
3.3.2 得證
ap - 1 
1(mod
p).

當 p| a 時 Ferma's Little Theorem 並不對, 因為此時
a  0(mod p), 故
ap - 1
0(mod p), 故
ap - 1  0(mod p).
不過我們可以推導出下一個對任意整數 a 皆成立的式子.
0(mod p).
不過我們可以推導出下一個對任意整數 a 皆成立的式子.
証 明.
因為
p 是質數所以對任意
a 

, 我們可以分成
p|
a 和
p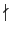 a
a 之情況處理. 當
p|
a 時, 由於
a 
0(mod
p), 故得
ap 
0
 a
a(mod
p). 當
p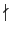 a
a 時, 由 Theorem
3.3.4 知
ap - 1 
1(mod
p), 故兩邊乘上
a 可得
ap  a
a(mod
p).



下一頁: Wilson's Theorem
上一頁: Congruences
前一頁: 同餘的運算
Li
2007-06-28
![]()
![]() , 若
a, b
, 若
a, b ![]()
![]() 滿足
ab
滿足
ab ![]() 1(mod m), 則由
Proposition 3.2.5 知 a 和 b 皆與 m 互質. 換言之,
我們只要考慮和 m 互質的數即可, 所以我們自然考慮 reduced residue
system modulo m.
1(mod m), 則由
Proposition 3.2.5 知 a 和 b 皆與 m 互質. 換言之,
我們只要考慮和 m 互質的數即可, 所以我們自然考慮 reduced residue
system modulo m.
![]() 1, 即存在一質數 p 滿足 p| m 且 p| ari.
因 p 是質數, 故由 Lemma 1.4.2 得 p| a 或 p| ri. 換言之,
p 為 m, a 的公因數或是 m, ri 的公因數. 此和
gcd(m, a) = 1 且
gcd(m, ri) = 1 相矛盾, 故得證
gcd(m, ari) = 1.
1, 即存在一質數 p 滿足 p| m 且 p| ari.
因 p 是質數, 故由 Lemma 1.4.2 得 p| a 或 p| ri. 換言之,
p 為 m, a 的公因數或是 m, ri 的公因數. 此和
gcd(m, a) = 1 且
gcd(m, ri) = 1 相矛盾, 故得證
gcd(m, ari) = 1.
![]() j 且
ari
j 且
ari ![]() arj(mod m), 則由
gcd(m, a) = 1, 利用 Corollary 3.2.4 得
ri
arj(mod m), 則由
gcd(m, a) = 1, 利用 Corollary 3.2.4 得
ri ![]() rj(mod m). 此和
ri
rj(mod m). 此和
ri ![]() rj(mod m) 矛盾, 故得證
ari
rj(mod m) 矛盾, 故得證
ari ![]() arj(mod m).
arj(mod m).
![]()
![]()
![]() , 利用除以 m 同餘的分類, 我們可以將與 m
互質的數分成
, 利用除以 m 同餘的分類, 我們可以將與 m
互質的數分成 ![]() (m) 類.
而將每一類中挑出一代表元素所成之集合就是一個 reduced residue system
modulo m. 今假若
S = {a1,..., a
(m) 類.
而將每一類中挑出一代表元素所成之集合就是一個 reduced residue system
modulo m. 今假若
S = {a1,..., a![]() (m)} 和
T = {b1,..., b
(m)} 和
T = {b1,..., b![]() (m)} 皆為 reduced residue system modulo
m, 任取 ai
(m)} 皆為 reduced residue system modulo
m, 任取 ai ![]() S, 由於它代表與 m 互質的某一同餘類, 而 T
中也有一元素是在和 ai 同類的元素中挑出. 換言之, 存在 bj
S, 由於它代表與 m 互質的某一同餘類, 而 T
中也有一元素是在和 ai 同類的元素中挑出. 換言之, 存在 bj ![]() T
滿足
ai
T
滿足
ai ![]() bj(mod m). 又由於這些 bj 兩兩皆不同類, 所以
S 和 T 中元素在 modulo m 之下有一對一的對應關係.
也就是說經過適當的排序, 我們有
ai
bj(mod m). 又由於這些 bj 兩兩皆不同類, 所以
S 和 T 中元素在 modulo m 之下有一對一的對應關係.
也就是說經過適當的排序, 我們有
ai ![]() bi(mod m). 因此得
a1 ... a
bi(mod m). 因此得
a1 ... a![]() (m)
(m) ![]() b1 ... b
b1 ... b![]() (m)(mod m).
利用這個結果我們可以得證 Euler's Theorem.
(m)(mod m).
利用這個結果我們可以得證 Euler's Theorem.
![]() (m)} 也是一個 reduced residue system modulo
m, 因此得
(m)} 也是一個 reduced residue system modulo
m, 因此得
![]()
![]() 及
a
及
a ![]()
![]() 滿足
gcd(m, a) = 1, 若令
b = a
滿足
gcd(m, a) = 1, 若令
b = a![]() (m) - 1, 則利用 Euler's Theorem 得知
ab
(m) - 1, 則利用 Euler's Theorem 得知
ab ![]() a
a![]() (m)
(m) ![]() 1(mod m). 因此我們找到了 a 在 modulo m
之下的乘法反元素.
1(mod m). 因此我們找到了 a 在 modulo m
之下的乘法反元素.
![]() 0(mod p), 故
ap - 1
0(mod p), 故
ap - 1 ![]() 0(mod p).
不過我們可以推導出下一個對任意整數 a 皆成立的式子.
0(mod p).
不過我們可以推導出下一個對任意整數 a 皆成立的式子.