Wilson's Theorem

當 p 是一個質數時, 若 p$\nmid$a, 則 Fermat's Little Theorem 告訴我們 a^{p - 2} 在 modulo p 之下是 a 的乘法反元素. 雖然 a 的乘法反元素在 modulo p 之下是唯一的, Wilson's Theorem 給了我們在 modulo p 之下 a 的乘法反元素的另一種表法.

給定 m $\in$ $\mathbb {N}$, 對於任意和 m 互質的整數 a, 由 Proposition 3.2.5 知都可以找到一個和 m 互質的整數 b 使得 ab $\equiv$ 1(mod m), 我們也提及雖然這樣的 b 並不唯一, 但在 modulo m 的分類之下它會是唯一的. 也就是說只有在除以 m 之下和 b 同餘的整數才會符合. 這種在 modulo m 之下乘法反元素的存在唯一性用 modulo m 之下的 reduced residue system 最容易表達.

Lemma 3.4.1   給定 m $\in$ $\mathbb {N}$, 假設 S = {r₁,..., r_$\phi$(m)} 是一個 reduced residue system modulo m. 則對於任意 r_i $\in$ S 皆存在唯一的 r_j $\in$ S 使得 r_ir_j $\equiv$ 1(mod m).

証 明. 因為 S 是一個 reduced residue system modulo m, 每一個 S 中的元素 s_i 皆和 m 互質, 故利用 Proposition 3.2.5 知存在 b $\in$ $\mathbb {Z}$ 使得 r_ib $\equiv$ 1(mod m). 由於 b 和 m 也是互質的, 故由 S 是一個 reduced residue system modulo m 之定義知必存在 r_j $\in$ S 和 b 在 modulo m 之下是同類的, 也就是說 b $\equiv$ r_j(mod m). 因此由 Lemma 3.1.3 知, r_ir_j $\equiv$ r_ib $\equiv$ 1(mod m). 證得存在性.

對於唯一性, 我們先假設 r_j, r_k $\in$ S 皆滿足 r_ir_j $\equiv$ 1(mod m) 以及 r_ir_k $\equiv$ 1(mod m). 因此得 r_ir_j $\equiv$ r_ir_k(mod m). 但由於 gcd(m, r_i) = 1, 利用 Corollary 3.2.4 得 r_j $\equiv$ r_k(mod m). 但 S 是 reduced residue system modulo m 表示 S 中相異的元素在 modulo m 之下應是不同類的, 故由 r_j $\equiv$ r_k(mod m) 知 r_j = r_k. 得證唯一性. $\qedsymbol$

例如 S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} 是一個 reduced residue system modulo 11, 在 modulo 11 之下我們有

1×1 $$\equiv$$ 2×6 $$\equiv$$ 3×4 $$\equiv$$ 5×9 $$\equiv$$ 7×8 $$\equiv$$ 10×10 $$\equiv$$ 1(mod 11).

在這個例子, S 中除了 1 和 10 以外其他的元素皆需與另外的元素相乘, 這在 modulo 一般的質數都是對的.

Lemma 3.4.2   給定一質數 p. 則 a $\in$ $\mathbb {Z}$ 滿足 a² $\equiv$ 1(mod p) 若且唯若 a $\equiv$ ±1(mod p).

証 明. 首先若 a $\equiv$ ±1(mod p), 則 a² $\equiv$ (±1)²(mod p). 得證 a² $\equiv$ 1(mod p).

反之, 若 a² $\equiv$ 1(mod p), 表示 p| a² - 1, 也就是說 p|(a - 1)(a + 1), 故因 p 是質數, 利用 Lemma 1.4.2 得 p| a - 1 或 p| a + 1. 也就是說 a $\equiv$ 1(mod p) 或 a $\equiv$ - 1(mod p). $\qedsymbol$

要注意 Lemma 3.4.2 在 modulo 一般的非質數之下就不一定對了, 例如在 modulo 15 之下除了 1 和 14 外, 還有 4 會滿足 4² $\equiv$ 1(mod 15), 而且很顯然的 4 $\not\equiv$±1 mod15. 所以要利用 Lemma 3.4.2, 我們必須限定在質數的情形, 此時我們可以得到 Wilson's Theorem.

Theorem 3.4.3 (Wilson's Theorem)   給定一質數 p. 設 {r₁,..., r_{p - 1}} 為一 reduced residue system modulo p. 則

r₁ ^... r_{p - 1} $$\equiv$$ - 1(mod p).

特別地, 我們有

(p - 1)! $$\equiv$$ - 1(mod p).

証 明. 若 p = 2, 則 modulo 2 之下的 reduced residue system 為 {r₁} 一個元素, 其中 r₁ $\equiv$ 1(mod 2). 但在 modulo 2 之下我們有 1 $\equiv$ - 1(mod 2), 故得證 r₁ $\equiv$ - 1(mod 2).

現考慮 p > 2 的情形, 令 S = {r₁,..., r_{p - 1}} 由於 gcd(p, 1) = gcd(p, - 1) = 1 且 1 $\not\equiv$ - 1(mod p) (否則 p| 2), 故分別存在 r_i, r_j $\in$ S 其中 r_i$\ne$r_j 滿足 r_i $\equiv$ 1(mod p) 且 r_j $\equiv$ - 1(mod p). 因此不失ㄧ般性, 我們可假設 r₁ $\equiv$ 1(mod p) 且 r₂ $\equiv$ - 1(mod p). 現考慮 r_i $\in$ S, 其中 3$\le$i$\le$p - 1. 依 Lemma 3.4.1 知存在唯一的 r_j $\in$ S 使得 r_ir_j $\equiv$ 1(mod p). 因為 r_i $\not\equiv$±1(mod p), 故知 r_j $\not\equiv$±1(mod p), 也就是說 3$\le$j$\le$p - 1. 又若 r_i = r_j, 會導致 r_i² $\equiv$ 1(mod p), 這與 Lemma 3.4.2 相矛盾, 故知 i$\ne$j. 也就是說在 T = {r₃,..., r_{p - 1}} 中任取一元素 r_i 必可找到唯一的另一元素 r_j $\in$ T 使得 r_ir_j $\equiv$ 1(mod p). 因此我們可以對 T 中這 p - 3 個元素兩兩配對 (注意 p 是奇數), 使得每一對中元素相乘後除以 p 會餘 1. 也就是說 r₃ ^... r_{p - 1} $\equiv$ 1(mod p). 因此我們得證

r₁r₂r₃ ^... r_{p - 1} $$\equiv$$ r₁r₂ $$\equiv$$ - 1(mod p).

最後由於 {1, 2,..., p - 1} 是一個 modulo p 的 reduced residue system, 故知

1×2× ^... ×(p - 1) = (p - 1)! $$\equiv$$ - 1(mod p).

$\qedsymbol$

若 p 是一質數且 a 是和 p 互質的整數, 我們可以利用 Wilson's Theorem 找到在 modulo p 之下, a 的乘法反元素. 由於當 a $\equiv$ ±1(mod p) 時 a² $\equiv$ 1(mod p), 也就是說 a 本身在 modulo p 之下是自己的乘法反元素, 所以我們僅討論 a $\not\equiv$±1(mod p) 的情況.

Corollary 3.4.4   給定一質數 p 及 a $\in$ $\mathbb {Z}$ 滿足 p$\nmid$a. 假設 a $\equiv$ i(mod p), 其中 2$\le$i$\le$p - 2. 若令

b = $${\frac{(p-2)!}{i}}$$

則 ab $\equiv$ 1(mod p).

証 明. 由於 2$\le$i$\le$p - 2, 我們知 b 是一個整數. 此時

ab $$\equiv$$ i$${\frac{(p-2)!}{i}}$$ $$\equiv$$ (p - 2)!(mod p)

又由於 (p - 1)! = (p - 1) ^. (p - 2)! 且 p - 1 $\equiv$ - 1(mod p), 故得證

ab $$\equiv$$ (p - 2)! $$\equiv$$ - ((p - 1)!) $$\equiv$$ 1(mod p).

$\qedsymbol$

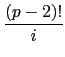
我們仍要強調一下雖然 Lemma 3.4.1 在一般的 m $\in$ $\mathbb {N}$ 都成立, 但 Lemma 3.4.2 需限制在質數時才成立, 所以 Wilson's Theorem 在 modulo 一般的 m 並不一定成立. 也就是說若 {r₁,..., r_$\phi$(m)} 是一個 reduced residue system modulo m, 並不一定可以得 r₁ ^... r_$\phi$(m) $\equiv$ - 1(mod m). 例如在 modulo 15 之下我們之還有 4 和 -4 滿足 4² $\equiv$ (- 4)² $\equiv$ 1(mod 15), 所以利用 Theorem 3.4.3 的證明方法 (或直接計算) 我們可得, 若 {r₁,..., r₈} 是一個 reduced residue system modulo 15, 則 r₁ ^... r₈ $\equiv$ 1(mod 15). 雖然利用 Theorem 3.4.3 的方法我們可以將 Wilson's Theorem 推廣到一般 m 的情形, 不過此時對一個 modulo m 的 reduced residue system {r₁,..., r_$\phi$(m)} 滿足 r_i² $\equiv$ 1(mod m) 的 r_i 會有很多種情形, 討論起來較複雜, 在這裡我們就不多探討了.