有關 Field Extension 的觀念

在這一節中我們希望說明一些觀念, 這些觀念說實話不容易講清楚, 如果同學無法完全了解也沒有關係, 可以依你所知的概念繼續研讀以下其他的章節. 等到對這些理論有更深一層的體認後或許就能慢慢體會這些觀念了.

在談論 field extension 時有一個很重要的定理, 這個定理是說: 如果 K 是一個 field, p(x) $\in$ K[x] 是一個 irreducible polynomial, 則必存在一個 K 的 extension field L 使得 p(x) = 0 在 L 中有解 (參見大學基礎代數講義 Theorem 10.3.4). 這個定理的證明大致上就是取 L = K[x]/(p(x)) 這個 field, 而 a = $\overline{x}$ $\in$ L 就是 p(x) 的一個根. 第一次看到這個證明大部分的同學會對這個簡單的證明充滿了疑惑, 大致上會有兩個疑問:

1. 怎麼找一個多項式的根那麼簡單? 為什麼高中時還要學那麼多解多項式方程式的方法?
2. 這裡的 K 真的包含於 L = K[x]/(p(x)) 嗎? $\overline{x}$ 真的是 p(x) = 0 的一個解嗎?

第一個問題比較好回答. 這個定理主要是存在性問題: 只要求找到一個 field 使的 p(x) = 0 在那個 field 中有解. 而從前高中找解是要求在特定的 field 中找解 (如 實數 $\mathbb {R}$ 或 複數 $\mathbb {C}$) 當然有其困難度. 別忘了這個世界不只有 $\mathbb {Q}$, $\mathbb {R}$, $\mathbb {C}$ 這三個 fields.

至於第二個問題較難回答, 我們用一個例子說明一下. 我們都知道 x³ - 2 是 $\mathbb {Q}$[x] 中的一個 irreducible polynomial. 如何找到一個 field 使得 x³ - 2 = 0 在其中有解呢? 假設你不知道這世上有 $\mathbb {R}$ 和 $\mathbb {C}$ 這個 field, 你會怎麼辦?

代數的方法就是先憑空找一個符號 a 假設是 x³ - 2 的根 (即 a 滿足 a³ = 2). 因為要找到一個 field L 使得 a 和 $\mathbb {Q}$ 都在裡面, 所以我們要求 a 和 $\mathbb {Q}$ 的元素都相互運算後仍在 L 中. 當然 $\mathbb {Q}$ 本身的運算還要保持, 所以我們只要注意 a 本身的自己的運算以及 a 和 $\mathbb {Q}$ 的運算即可. 首先對任意的 r $\in$ $\mathbb {Q}$, r + a 和 r ^. a 到底是什麼呢? 當 r = 0 時 r + a 和 r ^. a 當然須分別等於 a 和 0 這樣才能滿足結合率和分配率. 同樣的在結合率和分配率的要求之下當 r$\ne$ 0 時 r + a 和 r ^. a 都不能屬於 $\mathbb {Q}$, 所以我們的 L 中還必須包含 r + a 和 r ^. a 這兩種符號 (注意這仍只是符號而不是任何的數). 這裡要注意的是我們為了保持 1 仍為乘法單位元素所以必須把 1 ^. a 和 a 視為相同. 接下來我們看 a 本身的運算: a + a 和 a ^. a 應該是多少呢? 在要求分配率仍成立的前提下由於 a + a = 1 ^. a + 1 ^. a = (1 + 1) ^. a = 2 ^. a, 我們不需要新的符號來代表 a + a, 它就是 2 ^. a (簡記為 2a). 同樣的任意 n 個 a 相加就是 n ^. a. 至於 a ^. a 我們就需要新的符號, 按慣例就沿用指數的符號將 a ^. a 記為 a², 同樣的任意 n 個 a 相乘就記為 aⁿ. L 中若僅有這些符號還不夠成為一個 field (甚至連 ring 都不行), 我們還需要這些符號間的相加相乘. 很快的在分配率, 結合率以及交換率皆須符合的要求下我們發現 L 中必須有

r₀ + r₁ ^. a + r₂ ^. a² + ^... + r_n ^. aⁿ

這些符號, 其中 n 是任意非負整數, 而 r₀,..., r_n $\in$ $\mathbb {Q}$. 同樣的因為前述規律的要求這些符號之間的相加相乘就和多項式之間的相加相乘一樣 (現在應該可以看出前面那個定理的證明為何會和 K[x] 這個 polynomial ring 有關了吧). 事實上, 我們不需要這麼多符號: 這是因為我們要求 a³ = 2, 所以 a⁴ = 2a, a⁵ = 2a²,... 這樣一直下去我們發現前面那些符號都可以用

r₀ + r₁ ^. a + r₂ ^. a²

表示即可. 只用這些次數小於 3 的符號不止所用的符號少, 最重要的是它們的表法唯一. 換言之, 任兩個次數小於 3 的符號只要不相同它們就代表不同的數. 這方面前面任意次數的符號就沒有這優點 (比方說 a⁴ = 2a). 令一方面它們又足夠代表所有的符號: 這是因為 $\mathbb {Q}$ 是一個 field 我們可以用長除法 (Euclid's Algorithm 參見大學基礎代數講義 Theorem 7.2.4) 對任意 f (x) $\in$ $\mathbb {Q}$[x] 都可找到 h(x), r(x) $\in$ $\mathbb {Q}$[x] 使得 f (x) = (x³ - 2)h(x) + r(x) 其中 r(x) = 0 或其次數小於 3. 所以對任意的 f (a) 我們都可以用 r(a) 來表示 (現在大家應該可以看出當初為何會考慮 L = K[x]/(p(x)) 了). 只用到次數小於 3 的符號, 當定義加法時仍延用多項式的加法不會出問題 (因為兩次數小於 3 的多項式相加仍次數小於 3); 但是定義乘法若相乘後次數大於等於 3 怎麼辦? 當然我們就用上述長除法將次數大於等於 3 的符號用次數小於 3 的符號來表示了 (大家可以看出這裡的運算完全和 $\mathbb {Q}$[x]/(x³ - 2) 的運算相同). 所以集合

R = {r₀ + r₁ ^. a + r₂ ^. a² | r₀, r₁, r₂ $$\in$$ $$\mathbb {Q}$$}

在前述的運算之下就是包含 a 和 $\mathbb {Q}$ 且滿足 a³ = 2 最小的 ring. 事實上 R 會是一個 field, 這是由於若 f (x)$\ne$ 0, f (x) $\in$ $\mathbb {Q}$[x] 且 deg(f (x)) < 3, 則因 x³ - 2 是 $\mathbb {Q}$[x] 的 irreducible polynomial, f (x) 和 x³ - 2 必互質. 故由輾轉相除法 (或由 $\mathbb {Q}$[x] 是一個 principle ideal domain 參見大學基礎代數講義 Theorem 7.2.6) 知存在 g(x), h(x) $\in$ $\mathbb {Q}$[x] 其中 deg(g(x)) < 3, 使得 f (x)g(x) + (x³ - 2)h(x) = 1; 亦即 f (a) ^. g(a) = 1. 也就是說對任意 f (a)$\ne$ 0 且 f (a) $\in$ R 皆存在 g(a) $\in$ R 使得 f (a) ^. g(a) = 1. 所以 L = R 就是我們要找的 field. 現在可以相信 $\mathbb {Q}$ $\subseteq$ L 且 a $\in$ L 是 x³ - 2 的一個根了吧! 大家應該也可以看出這個 L 和 $\mathbb {Q}$[x]/(x³ - 2) 是 isomorphic. 但是要描述這個 L 裡元素間的運算多複雜啊! 還不如直接用 $\mathbb {Q}$[x]/(x³ - 2) 表示更簡明扼要.

了解了找到 extension 使的 x³ - 2 有根的建構方法後, 大家或許會有新的疑問: 我們都知道 x³ - 2 有 3 個根分別是

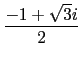$$\sqrt[3]{2}$$,    $$\sqrt[3]{2}$$ ($${\frac{-1+\sqrt{3} i}{2}}$$)    和    $$\sqrt[3]{2}$$ ($${\frac{-1-\sqrt{3} i}{2}}$$),

前面創造出的 a 到底是哪一個呢? 事實上都可以, 就看你怎樣把 a 送到 $\mathbb {C}$ 了. 你可以任取上述三個複數之ㄧ和 $\mathbb {Q}$ 中元素進行運算, 你會發現和 a 與 $\mathbb {Q}$ 中元素運算相同. 所以若有另一個人用 b 來表示 x³ - 2 的一個根, 然後用前述方法造出一個 field, 你不能說 a = b 但是可以肯定的是這兩個 field 是 isomorphic (都 isomorphic to $\mathbb {Q}$[x]/(x³ - 2)).

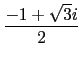或許你會有另一個疑問: 從上述觀點 x³ - 2 會有無窮多個根啊! 這不是和我們所認知的一個 n 次多項式至多有 n 個根 (大學基礎代數講義 Theorem 10.3.3) 相衝突嗎? 其實不然, 仔細看看大學基礎代數講義 Theorem 10.3.3 它其實是說在一個固定的 field 中至多有 n 個根. 這是一個很重要的概念: 在 Galois 理論中我們是要在一個固定的 field 中談問題. 雖然 field 是固定的但我們較不在意根長什麼樣子, 而重視的是在這 field 有幾個根. 例如 x³ - 2 在 $\mathbb {C}$ 中有三個相異根, 我們就得知有三種方法將 a 送到 $\mathbb {C}$ 中. 又例如 x³ - 2 在 $\mathbb {Q}$($\sqrt[3]{2}$) 中僅有一個根 (因為 $\mathbb {Q}$($\sqrt[3]{2}$) 中的元素都是實數, 但 x³ - 2 在 $\mathbb {C}$ 中其他兩個根是虛數) 所以我們知道將 a 送到 $\mathbb {C}$ 後所得的三個 fields 是相異的.

從上述的情況得知, 有些代數的性質和它的元素在於哪個 field 其實是無關的, 不過有時將之擺在一個固定的 field 中討論確有其方便性. 就例如對於 irreducible polynomial p(x) $\in$ K[x] 我們考慮 L = K[x]/(p(x)) 使得 p(x) 在 L 中有根. 在這裡 K 其實並不是真正包含於 L 中, 我們只是找到ㄧ個一對一的 ring homomorphism 將 K 送到 L 中. 因為這時候這個 ring homomorphism 的像 (image) 和 K 的代數結構是一樣的而且是 L 的 subfield 所以我們就視同 K 包含於 L. 事實上我們有以下一個比較正式的定義:

Definition 1.1.1   假設 K 和 L 都是 fields 且 K 和 L 間存在ㄧ對一的 ring homomorphism i : K$\to$L, 則稱 L 是 K 的 extension. 通常我們會記作 L/K (唸成 L over K).

簡單來說就是當 K 並不包含於 L 時, 我們當然不能直接對 K 的元素和 L 的元素做運算. 不過如果存在一對一的 ring homomorphism i : K$\to$L, 那麼對任意的 k $\in$ K 和 l $\in$ L, 我們可以定

k + l : = i(k) + l    and    k ^. l : = i(k) ^. l,

因為 i(k) $\in$ L 所以自然可以和 L 中的元素做運算了. 又因為 i 是一對一的, i 的像 i(K) = {i(k) | k $\in$ K} 中的元素和 K 中的元素有一個一對一的對應關係. 因此我們可以將 K 中的元素 (k $\in$ K) 看成是是 L 的元素 (i(k) $\in$ L). 也就是說我們將 K ``identify'' 成 L 的ㄧ個 subfield. 因此從今以後我們若提到 L 是 K 的 extension 為了方便我們還是省略提及存在一個 i : K$\to$L, 而直接假設 K $\subseteq$ L.

Galois 理論簡單的說就是探討 field extensions 間的關係. 給定一個 field K, 事實上存在無窮多個 K 的 extensions, 我們自然會問兩個 extensions L₁/K 和 L₂/K 在什麼條件之下可以看成是一樣的 extension 呢？這不是單純的兩個 fields L₁ 和 L₂ 間的關係, 還牽涉到 K 在 L₁ 和 L₂ 中的“角色” . 簡單來說, 我們不只希望 L₁ 和 L₂ 是 isomorphic 而且希望能保持 K 的運算. 因此我們有以下的定義:

Definition 1.1.2   令 i : K$\to$L₁, j : K$\to$L₂ 是 K 的兩個 extensions. 如果存在 $\phi$ : L₁$\to$L₂ 是一個 isomorphism 滿足對任意的 k $\in$ K 皆有 $\phi$(i(k)) = j(k), 則稱 L₁/K 和 L₂/K 是 isomorphic extensions over K.

這裡因為 k $\in$ K 所以 i(k) $\in$ L₁. 因此 $\phi$ 可將 i(k) 送到 L₂ 中. 而 $\phi$(i(k)) = j(k) 就是要求 $\phi$ 必須把在 L₁ 中代表 k 的元素送到 L₂ 中那個代表 k 的元素. 特別的是當我們將 K 分別看成是 L₁ 和 L₂ 的 subfield (即 K $\subseteq$ L₁ 且 K $\subseteq$ L₂), 此時 i(k) = k 且 j(k) = k 因此 $\phi$ 必須符合對於所有的 k $\in$ K, 皆滿足 $\phi$(k) = k. 在這情況之下有這樣性質的 $\phi$ 就稱為 L₁ 和 L₂ 之間的一個 ``K-isomorphism''. 特別是當 L<sub>1</sub> = L<sub>2</sub> 時我們稱 $\phi$ 為一個 ``K-automorphism''. 一般為了方便起見, 兩個 extensions L₁/K 和 L₂/K 我們都直接看成 K $\subseteq$ L₁ 和 K $\subseteq$ L₂. 所以若 L₁/K 和 L₂/K 是 isomorphic extensions over K 我們就直接假設 L₁ 和 L₂ 之間存在一個 K-isomorphism.