


下一頁: Field Extensions 的分類
上一頁: Field Extensions
前一頁: 有關 Field Extension 的觀念
目 錄
在大學基礎代數講義的 Chapter 9 Section 4 中我們曾經說明若 L/K
是一個 field extension 那麼我們可以將 L 看成是一個 vector space
over K. 這件事情在我們新的 field extension 的定義之下仍是對的.
也就是說若 i : K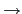 L 是一個 field extension, 那麼仿照前面對任意的
k
L 是一個 field extension, 那麼仿照前面對任意的
k  K 及 l
K 及 l  L 我們定義
k . l : = i(k) . l,
很容易就可以驗證在此定義之下 L 仍為一個 vector space over K.
既然 L 是一個 vector space over K, 很自然的會考慮到其維度
(dimension) 因此我們仍然有以下的定義:
L 我們定義
k . l : = i(k) . l,
很容易就可以驗證在此定義之下 L 仍為一個 vector space over K.
既然 L 是一個 vector space over K, 很自然的會考慮到其維度
(dimension) 因此我們仍然有以下的定義:
Definition 1.2.1
給定一個 field extension L/K, 我們用 [L : K] 來表示 dimK(L),
稱之為 the degree of L over K. 若 [L : K] 是有限的 (即 L
是一個 finite dimensional vector space over K), 則稱 L 是 K
的一個 finite extension.
若 L1/K 和 L2/K 是兩個 isomorphic extensions over K, 由
extension degree 的定義大家應可理解
[L1 : K] = [L2 : K].
這個證明很簡單不過我們仍將證明寫下讓大家了解當初要求 isomorphism
時要保持 K 的重要性.
Lemma 1.2.2
若
L1/
K 和
L2/
K 是兩個 isomorphic extensions over
K, 則
[
L1 :
K] = [
L2 :
K].
証 明.
大家可以直接假設
K  L1
L1 和
K  L2
L2 來處理,
這裡我們用比較正式的定義來證明.
假設
i : K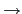 L1 和
j : K
L1 和
j : K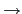 L2 分別為 L1/K 和 L2/K 的
extension 且
L2 分別為 L1/K 和 L2/K 的
extension 且
 : L1
: L1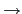 L2 為 L1 和 L2 的 isomorphism over
K. 依定義
L2 為 L1 和 L2 的 isomorphism over
K. 依定義  是一個 ring homomorphism, 如果我們能證明
是一個 ring homomorphism, 如果我們能證明  是 L1 和 L2 這兩個 vector space over K 的 K-linear map,
那麼再由假設
是 L1 和 L2 這兩個 vector space over K 的 K-linear map,
那麼再由假設  是 1-1 且 onto (因已知
是 1-1 且 onto (因已知  是 isomorphism)
可得
dimK(L1) = dimK(L2), 即
[L1 : K] = [L2 : K].
是 isomorphism)
可得
dimK(L1) = dimK(L2), 即
[L1 : K] = [L2 : K].
要證明  是 K-linear, 只要證明對任意的 c
是 K-linear, 只要證明對任意的 c  K 且
a, b
K 且
a, b  L1, 皆有
L1, 皆有
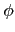
(
c . a +
b) =
c . 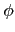
(
a) +
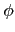
(
b).
這裡的
c . a +
b 需看成是
L1 中元素的運算, 依定義是
i(
c)
. a +
b.
故利用

是
L1 到
L2 的 ring homomorphism 知
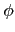
(
c . a +
b) =
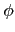
(
i(
c)
. a +
b) =
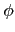
(
i(
c)
. a) +
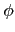
(
b) =
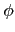
(
i(
c))
. 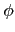
(
a) +
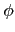
(
b).
另一方面,
c . 
(
a) +

(
b) 需看成是
L2 中元素的運算, 依定義是
j(
c)
. 
(
a) +

(
b). 然而

滿足

(
i(
c)) =
j(
c) 故知

(
c . a +
b) =
c . 
(
a) +

(
b), 也就是說

是一個
K-linear map.
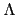
從這個證明我們了解到若  是 L1 到 L2 的 ring homomorphism
且保持 K 的運算那麼
是 L1 到 L2 的 ring homomorphism
且保持 K 的運算那麼  就是一個 L1 到 L2 的 K-linear
map. 不過反過來並不一定對. 也就是說如果
就是一個 L1 到 L2 的 K-linear
map. 不過反過來並不一定對. 也就是說如果
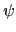 : L1
: L1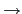 L2 是一個
K-linear map 並不一定保證
L2 是一個
K-linear map 並不一定保證 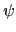 是一個 ring homomorphism.
這是由於 K-linear map 僅保持 K 中元素和 L1
中元素的乘法運算但是 ring homomorphism 卻需保持任兩個 L1
中元素的乘法運算. 因此要注意兩個 extensions L1/K 和 L2/K,
如果僅知
[L1 : K] = [L2 : K] 並不表示 L1 和 L2 是 isomorphic
extensions over K.
是一個 ring homomorphism.
這是由於 K-linear map 僅保持 K 中元素和 L1
中元素的乘法運算但是 ring homomorphism 卻需保持任兩個 L1
中元素的乘法運算. 因此要注意兩個 extensions L1/K 和 L2/K,
如果僅知
[L1 : K] = [L2 : K] 並不表示 L1 和 L2 是 isomorphic
extensions over K.
若 L, F 和 K 皆為 fields, 且 i : K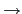 F 和 j : F
F 和 j : F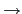 L 皆為 1-1
的 ring homomorphism, 則
joi : K
L 皆為 1-1
的 ring homomorphism, 則
joi : K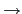 L 當然也是 1-1 的 ring
homomorphism. 所以如果 L/F 和 F/K 是 field extensions 則 L
當然也是一個 field extension of K. 我們有以下重要有關 extension
degree 的性質. 事實上這是大學基礎代數講義的 Theorem 9.4.6 和
Corollary 9.4.7 的合併, 我們就不再證明了.
L 當然也是 1-1 的 ring
homomorphism. 所以如果 L/F 和 F/K 是 field extensions 則 L
當然也是一個 field extension of K. 我們有以下重要有關 extension
degree 的性質. 事實上這是大學基礎代數講義的 Theorem 9.4.6 和
Corollary 9.4.7 的合併, 我們就不再證明了.
Lemma 1.2.3
假設
L/
F 和
F/
K 是 field extensions.
若
F 是
K 的一個 finite extension 且
L 是
F 的一個 finite
extension 則
L 也是
K 的一個 finite extension. 反之, 若
L 是
K 的一個 finite extension, 則
F 是
K 的一個 finite extension
且
L 是
F 的一個 finite extension.
另外, 在這兩個等價條件之下皆有:
[L : K] = [L : F][F : K].



下一頁: Field Extensions 的分類
上一頁: Field Extensions
前一頁: 有關 Field Extension 的觀念
目 錄
Li
2006-05-18
![]() L1 和
j : K
L1 和
j : K![]() L2 分別為 L1/K 和 L2/K 的
extension 且
L2 分別為 L1/K 和 L2/K 的
extension 且
![]() : L1
: L1![]() L2 為 L1 和 L2 的 isomorphism over
K. 依定義
L2 為 L1 和 L2 的 isomorphism over
K. 依定義 ![]() 是一個 ring homomorphism, 如果我們能證明
是一個 ring homomorphism, 如果我們能證明 ![]() 是 L1 和 L2 這兩個 vector space over K 的 K-linear map,
那麼再由假設
是 L1 和 L2 這兩個 vector space over K 的 K-linear map,
那麼再由假設 ![]() 是 1-1 且 onto (因已知
是 1-1 且 onto (因已知 ![]() 是 isomorphism)
可得
dimK(L1) = dimK(L2), 即
[L1 : K] = [L2 : K].
是 isomorphism)
可得
dimK(L1) = dimK(L2), 即
[L1 : K] = [L2 : K].
![]() 是 K-linear, 只要證明對任意的 c
是 K-linear, 只要證明對任意的 c ![]() K 且
a, b
K 且
a, b ![]() L1, 皆有
L1, 皆有