


下一頁: Galois Group 和 Fixed
上一頁: Field Extensions
前一頁: Field Extension 的 Degree
目 錄
要創造出一 field extension over K 通常就是在 K 中加入其他的元素.
當然不能隨便亂加東西, 因為我們要求 field extension 仍然要是一個
field 所以加入的東西至少和 K 之間要可以運算.
有一種情況我們是不必擔心加入的東西和 K 是否能運算,
就是當這些東西和 K 都可以在某個更大的 field L 之中,
在這情況之下我們當然可以把所有的元素看成是 L 的元素,
自然就可以運算了. 當然了加入的元素雖然可以運算最後還需成為一個
field, 要達到這個目的我們有以下這個定義:
Definition 1.3.1
若
L 是一個 field,
K  L
L 是
L 的 subfield 且
S  L
L 是
F 的ㄧ個子集合 (subset). 我們定義
K(
S) 為
L
中所有包含
K 和
S 的 subfields 的交集. 也就是說
K(
S) =
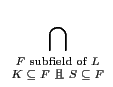 F
F.
稱為 the
extension of K generated by S.
這裡要注意:如同證明一個 ring 中的一些 subrings 的交集仍為 ring
(參見大學基礎代數講義 Lemma 6.2.2) 的方法, 我們可以證得一個 field
中的一些 subfields 的交集仍為 field. 所以 K(S) 也是一個 field.
由這個定義也可以看出 K(S) 事實上是 L 中包含 K 和 S 最小的
field. 換句話說:如果 K' 是 L 的 subfield 且
K  K'
以及
S
K'
以及
S  K', 則可得
K(S)
K', 則可得
K(S)  K'.
K'.
當
S = {a1,..., an} 是 F 的ㄧ個有限子集時,
我們通常會省略``{ }'' 這個符號而將 K(S) 記為
K(a1,..., an). 特別是當 S = {a} 只有一個元素時我們稱 K(a) 是 K
的一個 simple extension.
不難理解 simple extensions 是了解 field extensions 的要素. Simple
extension 不只是最簡單的 extension 而且我們這裡要學習的 extensions
(特別是 finite extensions) 大部分都可以利用 simple extensions
一步一步 extend 上去而得到. 所以如果能了解 simple extensions
大致上就能了解一般的 extensions. 我們自然得花點時間了解一下 simple
extensions.
利用 a 得到的 simple extension K(a) 可以分成兩種情況: 一種是
[K(a) : K] 是 finite 的情況; 另一種是 [K(a) : K] 是 infinite 的情況.
Definition 1.3.2
如果 K(a)/K 是一個 finite extension 則稱 a 是 algebraic
over K; 反之則稱 a 是 transcendental over K.
這個定義其實和以前學過 algebraic 的定義 (大學基礎代數講義 Definition
9.4.4) 是等價的. 這是由於我們有以下的性質.
Theorem 1.3.3
假設
K 是一個 field,
L 是
K 的一個 extension field 且
a  L
L, 則下面任一敘述和
a 是 algebraic over
K 是等價的.
- 存在 K[x] 中的一個非 0 的 polynomial f (x) 滿足
f (a) = 0.
- 存在一個 field M 滿足 a
 M,
K
M,
K  M
M  L 且 [M : K] 是有限的.
L 且 [M : K] 是有限的.
- 在 L 中包含 K 和 a 最小的 ring (即 K[a]) 就是包含 K 和 a 最小的 field (即
K[a] = K(a)).
証 明.
(1), (2) 和 (3) 是等價的我們已在大學基礎代數講義 Theorem 10.1.9
中證明過了 (注意那時是用 (1) 來定義 algebraic). 這裡我們只要檢查
a
是 algebraic over
K (即 [
K(
a) :
K] 是有限的) 和 (2) 是等價的即可.
如果 [K(a) : K] 是有限的, 則令 M = K(a), 故有 a  M,
K
M,
K  M
M  L 且 [M : K] 是有限的.
L 且 [M : K] 是有限的.
反之, 如果 M 是一個 field 滿足 a  M,
K
M,
K  M
M  L 且 [M : K] 是有限的, 則由 K(a) 是 L 中包含 K 和 a 最小的
field 的定義知
K
L 且 [M : K] 是有限的, 則由 K(a) 是 L 中包含 K 和 a 最小的
field 的定義知
K  K(a)
K(a)  M. 也就是說 K(a) 是 M
over K 的一個 subspace. 所以由線性代數知其 over K 的 dimension
一定比較小, 也就是說
[K(a) : K]
M. 也就是說 K(a) 是 M
over K 的一個 subspace. 所以由線性代數知其 over K 的 dimension
一定比較小, 也就是說
[K(a) : K] 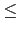 [M : K]. 故知 [K(a) : K] 是有限的.
[M : K]. 故知 [K(a) : K] 是有限的.
回顧一下, 當 a 是 algebraic over K 時滿足 Theorem 1.3.3
(1) 中所述次數最小的 monic polynomial (即最高次項係數為 1) 稱為 a
over K 的 minimal polynomial. (注意這裡一定要強調 over
哪一個 field 的 minimal polynomial, 因為 over 不同的 field 其
minimal polynomial 會不同.) 如果 a over K 的 minimal polynomial
為 p(x) 且
deg(p(x)) = n, 那麼我們有以下重要的結論:
- K(a) 和
K[x]/(p(x)) 是 isomorphic extensions over K.
-
[K(a) : K] = n.
- K(a) 中的元素的可以唯一表示成
c0 +
c1a +
... +
cn - 1an - 1, 其中
c0,
c1...,
cn - 1  K
K.
當 b  L 也滿足 p(b) = 0 時, 不見得會有 K(a) = K(b). 但由前面 (1)
得知 K(a) 和 K(b) 都和
K[x]/(p(x)) 是 isomorphic extensions
over K, 所以我們知 K(a) 和 K(b) 是 isomorphic extensions over
K. 事實上若我們定
L 也滿足 p(b) = 0 時, 不見得會有 K(a) = K(b). 但由前面 (1)
得知 K(a) 和 K(b) 都和
K[x]/(p(x)) 是 isomorphic extensions
over K, 所以我們知 K(a) 和 K(b) 是 isomorphic extensions over
K. 事實上若我們定
 : K(a)
: K(a)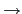 K(b) 滿足
K(b) 滿足
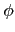
(
c0 +
c1a +
... +
cn - 1an - 1) =
c0 +
c1b +
... +
cn - 1bn - 1,
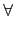 c0
c0,
c1,...,
cn - 1 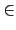 K
K,
則  就是一個 K(a) 到 K(b)
的 K-isomorphism. 要注意的是在更一般的情況, 如果
q(x)
就是一個 K(a) 到 K(b)
的 K-isomorphism. 要注意的是在更一般的情況, 如果
q(x)  K[x] 是
c
K[x] 是
c  L 的 minimal polynomial over K 且
p(x)
L 的 minimal polynomial over K 且
p(x)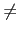 q(x),
那麼我們不能馬上斷言 K(a) 和 K(c) 是否 isomorphic over K.
當然了如果
deg(p(x))
q(x),
那麼我們不能馬上斷言 K(a) 和 K(c) 是否 isomorphic over K.
當然了如果
deg(p(x))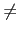 deg(q(x)), 由於
[K(a) : K]
deg(q(x)), 由於
[K(a) : K]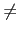 [K(c) : K]
利用 Lemma 1.2.2 我們立刻知 K(a) 和 K(c) 不可能是
isomorphic extensions over K. 但當
deg(p(x)) = deg(q(x)) 時,
雖然
[K(a) : K] = K[(c) : K], 我們曾解釋過此時並不保證 K(a) 和 K(c)
是 isomorphic over K. 有很多種情況它們是不 isomorphic, 不過當 K
是 finite field 時, K(a) 和 K(c) 確實會 isomorphic over K
(事實上是 K(a) = K(c) 參見大學基礎代數講義 Theorem 10.4.8).
[K(c) : K]
利用 Lemma 1.2.2 我們立刻知 K(a) 和 K(c) 不可能是
isomorphic extensions over K. 但當
deg(p(x)) = deg(q(x)) 時,
雖然
[K(a) : K] = K[(c) : K], 我們曾解釋過此時並不保證 K(a) 和 K(c)
是 isomorphic over K. 有很多種情況它們是不 isomorphic, 不過當 K
是 finite field 時, K(a) 和 K(c) 確實會 isomorphic over K
(事實上是 K(a) = K(c) 參見大學基礎代數講義 Theorem 10.4.8).
如果 L/K 是一個 extension 且 L 中所有的元素都是 algebraic over
K, 我們便稱 L 是一個 algebraic extension over K. 當
L/K 是 finite extension, 由 Theorem 1.3.3 (2) 知 L/K
必為 algebraic extension. 不過要注意 algebraic extension 不一定會是
finite extension. 比方說
 (S) 其中
S = {
(S) 其中
S = {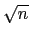 | n
| n 
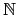 },
就是一個 algebraic extension over
},
就是一個 algebraic extension over
 但不是 finite extension over
但不是 finite extension over
 . 另一方面當 S 是一個有限集合時, K(S)/K 也未必是
finite extension, 除非 S 中的元素都是 algebraic over K.
我們有以下有關 finite extension 的充要條件.
. 另一方面當 S 是一個有限集合時, K(S)/K 也未必是
finite extension, 除非 S 中的元素都是 algebraic over K.
我們有以下有關 finite extension 的充要條件.
Proposition 1.3.4
若
S 是一個 finite set 且
S 中的元素皆 algebraic over
K, 則
L =
K(
S) 是一個 finite extension over
K.
反之, 若 L/K 是一個 finite extension, 則必存在一個 finite set S
其中 S 的元素皆 algebraic over K, 使得 L = K(S).
証 明.
首先我們觀察若
F/
K 是一個 extension 且
a 是 algebraic over
K
則
a 是 algebraic over
F. 這是由於 Theorem
1.3.3
告訴我們存在
f (
x)
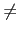
0 且
f (
x)
 K
K[
x] 滿足
f (
a) = 0. 但由於
K  F
F 所以知
f (
x)
 F
F[
x], 故再利用 Theorem
1.3.3 的等價關係知
a 仍為 algebraic over
F.
現在如果
S = {a1,..., an} 且
a1,..., an 皆 algebraic over
K, 對任意
i  {1,..., n} 我們令
Fi = K(a1,..., ai). 由於
L = K(a1,..., an) = Fn 以及
Fi
{1,..., n} 我們令
Fi = K(a1,..., ai). 由於
L = K(a1,..., an) = Fn 以及
Fi  Fi + 1, 利用 Lemma
1.2.3 我們有
Fi + 1, 利用 Lemma
1.2.3 我們有
[L : K] = [K(a1,..., an) : K] = [Fn : Fn - 1] ... [F2 : F1] . [F1 : K].
由於
F1 =
K(
a1) 且
a1 是 algebraic over
K 故知 [
F1 :
K]
是有限的. 同理, 當
i 
{1,...,
n - 1} 時, 由於
Fi + 1 =
Fi(
ai + 1) 且
ai + 1 是 algebraic over
Fi (因
ai + 1 是 algebraic over
K 且
K  Fi
Fi), 故知
[
Fi + 1 :
Fi] 是有限的. 因此得到 [
L :
K] 是有限的, 即
L/
K 是一個
finite extension.
反之, 如果 L/K 是 finite extension, 我們對 extension degree 作
induction. 也就是對任意的 extension L'/K' 假設當 [L' : K'] < m 時,
皆存在一個 finite set S', 使得 L' = K'(S'). 當 [L : K] = 1 時, 由於
L = K, 我們可以令 S = {1} 即可. 現若 [L : K] = m, 任取 a  L 但
a
L 但
a 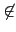 K. 由於
[L : K] = [L : K(a)][K(a) : K], 馬上得知
[L : K(a)] < m
(因
a
K. 由於
[L : K] = [L : K(a)][K(a) : K], 馬上得知
[L : K(a)] < m
(因
a 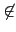 K, 故
[K(a) : K] > 1) 故由 induction 的假設知存在一個
finite set S' 使得
L = K(a)(S'). 故令
S = S'
K, 故
[K(a) : K] > 1) 故由 induction 的假設知存在一個
finite set S' 使得
L = K(a)(S'). 故令
S = S' 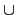 {a}, 則知 S
是一個 finite set 且 L = K(S). 這裡 S 中的元素必定會 algebraic
over K, 這是因為 L/K 是 finite extension 所以 L 中的元素必皆
algebraic over K.
{a}, 則知 S
是一個 finite set 且 L = K(S). 這裡 S 中的元素必定會 algebraic
over K, 這是因為 L/K 是 finite extension 所以 L 中的元素必皆
algebraic over K.
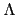
在 Theorem 1.3.3 中我們提過: 當 a 是 algebraic over K
且 L = K(a) 時, 包含 a 和 K 最小的 ring, K[a] 事實上就是 L.
當 L/K 是 finite extension 時, 由 Proposition 1.3.4 知存在
a1,..., an 皆 algebraic over K 使得
L = K(a1,..., an).
我們自然會問: 是否包含 K 和
a1,..., an 最小的 ring,
K[a1,..., an] 會是 L 呢? 由於
K  K[a1,..., an]
K[a1,..., an]  L, 我們知
K[a1,..., an] 是 L over
K 的 subspace, 故知
dimK(K[a1,..., an])
L, 我們知
K[a1,..., an] 是 L over
K 的 subspace, 故知
dimK(K[a1,..., an])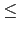 [L : K]
因此由大學基礎代數講義Theorem 9.3.7 馬上就知
K[a1,..., an] 是一個
field, 故知
K[a1,..., an] = L. 這裡我們想用 induction 來證明,
讓大家更清楚這個結果.
[L : K]
因此由大學基礎代數講義Theorem 9.3.7 馬上就知
K[a1,..., an] 是一個
field, 故知
K[a1,..., an] = L. 這裡我們想用 induction 來證明,
讓大家更清楚這個結果.
Lemma 1.3.5
假設
L/
K 是一個 finite extension. 若
L =
K(
a1,...,
an), 則包含
K 和
a1,...,
an 最小的 ring,
K[
a1,...,
an] 等於
L.
也就是說對任意

 L
L, 皆存在一個
n 個變數的 polynomial,
f (
x1...,
xn)
 K
K[
x1,...,
xn] 滿足
f (
a1,...,
an) =

.
証 明.
我們對
n 做 induction. 當
n = 1 時, 利用 Theorem
1.3.3
知對任意

 K
K(
a1) 都存在
c0,
c1,...,
cr  K
K 使得

=
c0 +
c1a1 +
... +
cra1r. 令
f (
x) =
c0 +
c1x +
... +
crxr, 可得

=
f (
a1). 利用 induction, 假設
F =
K(
a1,...,
an - 1) 且對任意
F 中的元素
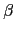
皆存在
f (
x1,...,
xn - 1)
 K
K[
x1,...,
xn - 1] 滿足
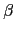
=
f (
a1,...,
an - 1). 考慮
L =
K(
a1,...,
an - 1,
an) =
F(
an). 由於
an 是 algebraic over
K  F
F, 再利用 Theorem
1.3.3 知對任意

 L
L 都存在
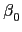
,
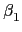
,...,
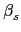
 F
F 使得

=
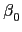
+
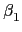 an
an +
... +
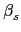 ans
ans. 然而
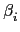
 F
F, 由 induction 的假設知對每一個
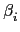
皆存在
fi(
x1 ... ,
xn - 1)
 K
K[
x1,...,
xn - 1] 使得
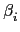
=
fi(
a1,...,
an - 1). 故若令
f (
x1,...,
xn - 1,
xn)
為
f0(
x1,...,
xn - 1) +
f1(
x1,...,
xn - 1)
xn +
... +
fs(
x1,...,
xn - 1)
xns 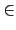 K
K[
x1,...,
xn - 1,
xn],
我們有

=
f (
a1,...,
an - 1,
an).
當 L/K 不是 algebraic extension 時, 依定義在 L 中必存在一元素
a 是 transcendental over L. 換言之, K(a)/K 不是 finite
extension. 最後我們簡單的介紹一下這一種 simple extension. a 是
transcendental over K 意即對任意的非零的多項式
f (x)  K[x] 皆有
f (a)
K[x] 皆有
f (a)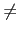 0. 由於 K(a) 是一個包含 K 和 a 的 field, 對任意
f (x)
0. 由於 K(a) 是一個包含 K 和 a 的 field, 對任意
f (x)  K[x], f (a) 當然也在 K(a) 中. 事實上
K[x], f (a) 當然也在 K(a) 中. 事實上
K[
a] = {
f (
a) |
f (
x)
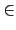 K
K[
x]}
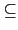 K
K(
a)
是包含 K 和 a
最小的 ring. 這個性質和 a 是 algebraic 或 transcendental over K
無關. 不過由於 a 是 transcendental over K, 若
f (x), g(x)  K[x] 且
f (x)
K[x] 且
f (x)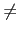 g(x), 則
f (a)
g(x), 則
f (a)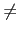 g(a). 這是因為 f (x) - g(x) 是
K[x] 中非 0 的多項式, 如果 f (a) = g(a) 這表示 a 為 f (x) - g(x)
的一個根, 此與 a 是 transcendental over K 相矛盾. 這和 algebraic
over K 的情況不同, 因為若 b 是 algebraic over K 且
p(x)
g(a). 這是因為 f (x) - g(x) 是
K[x] 中非 0 的多項式, 如果 f (a) = g(a) 這表示 a 為 f (x) - g(x)
的一個根, 此與 a 是 transcendental over K 相矛盾. 這和 algebraic
over K 的情況不同, 因為若 b 是 algebraic over K 且
p(x)  K[x] 是其 minimal polynomial over K, 則對任意的
f (x)
K[x] 是其 minimal polynomial over K, 則對任意的
f (x)  K[x]
我們都可以找到
g(x) = f (x) + p(x)
K[x]
我們都可以找到
g(x) = f (x) + p(x)  K[x] 使得
f (x)
K[x] 使得
f (x)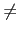 g(x) 但是
f (b) = g(b). 另一個 algebraic 和 transcendental 不同的是: 當 b 是
algebraic over K 時包含 K 和 b 最小的 ring 也會是一個 field
(即 K[b] = K(b)); 不過若 a 是 transcendental over K, 那麼包含
K 和 a 最小的 ring (即 K[a]) 就不再是一個 field 了. 這是因為當
f (x)
g(x) 但是
f (b) = g(b). 另一個 algebraic 和 transcendental 不同的是: 當 b 是
algebraic over K 時包含 K 和 b 最小的 ring 也會是一個 field
(即 K[b] = K(b)); 不過若 a 是 transcendental over K, 那麼包含
K 和 a 最小的 ring (即 K[a]) 就不再是一個 field 了. 這是因為當
f (x)  K[x] 且
deg(f (x))
K[x] 且
deg(f (x))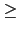 1 時, f (a)
1 時, f (a)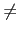 0 且如果存在
g(a)
0 且如果存在
g(a)  K[a] 使得
f (a) . g(a) = 1 表示 a 是
f (x) . g(x) - 1 的一個根, 再次和 a 是 transcendental over K 相矛盾.
因此我們知 K[a] 不可能是 field. 那麼 K(a) 到底是怎樣的 field 呢?
事實上若考慮
K[a] 使得
f (a) . g(a) = 1 表示 a 是
f (x) . g(x) - 1 的一個根, 再次和 a 是 transcendental over K 相矛盾.
因此我們知 K[a] 不可能是 field. 那麼 K(a) 到底是怎樣的 field 呢?
事實上若考慮
L = {
f (
a)/
g(
a) |
f (
x),
g(
x)
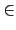 K
K[
x] 且
g(
x)
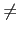
0}
很容易驗證這是包含 K 和 a 最小的 field, 故有 K(a) = L.
同樣的道理, 如果
L = K(a1,..., an), 其中某些 ai 是
transcendental over K, 那麼 L 中的元素並不能全部用
f (a1,..., an) 其中
f (x1,..., xn)  K[x1,..., xn],
這種形式來表示. 但是要描述 L 中的元素, 我們仍可用
f (a1,..., an)/g(a1,..., an), 其中
f (x1,..., xn), g(x1,..., xn)
K[x1,..., xn],
這種形式來表示. 但是要描述 L 中的元素, 我們仍可用
f (a1,..., an)/g(a1,..., an), 其中
f (x1,..., xn), g(x1,..., xn)  K[x1,..., xn] 且
g(a1,..., an)
K[x1,..., xn] 且
g(a1,..., an)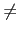 0
來表示. 在本講義中我們僅探討 finite extension, 所以對於
transcendental extension 我們僅探討到此.
0
來表示. 在本講義中我們僅探討 finite extension, 所以對於
transcendental extension 我們僅探討到此.



下一頁: Galois Group 和 Fixed
上一頁: Field Extensions
前一頁: Field Extension 的 Degree
目 錄
Li
2006-05-18
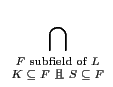 F.
F.
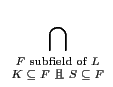 F.
F.
![]() M,
K
M,
K ![]() M
M ![]() L 且 [M : K] 是有限的.
L 且 [M : K] 是有限的.
![]() M,
K
M,
K ![]() M
M ![]() L 且 [M : K] 是有限的, 則由 K(a) 是 L 中包含 K 和 a 最小的
field 的定義知
K
L 且 [M : K] 是有限的, 則由 K(a) 是 L 中包含 K 和 a 最小的
field 的定義知
K ![]() K(a)
K(a) ![]() M. 也就是說 K(a) 是 M
over K 的一個 subspace. 所以由線性代數知其 over K 的 dimension
一定比較小, 也就是說
[K(a) : K]
M. 也就是說 K(a) 是 M
over K 的一個 subspace. 所以由線性代數知其 over K 的 dimension
一定比較小, 也就是說
[K(a) : K] ![]() [M : K]. 故知 [K(a) : K] 是有限的.
[M : K]. 故知 [K(a) : K] 是有限的.
![]()
![]() (S) 其中
S = {
(S) 其中
S = {![]() | n
| n ![]()
![]() },
就是一個 algebraic extension over
},
就是一個 algebraic extension over
![]() 但不是 finite extension over
但不是 finite extension over
![]() . 另一方面當 S 是一個有限集合時, K(S)/K 也未必是
finite extension, 除非 S 中的元素都是 algebraic over K.
我們有以下有關 finite extension 的充要條件.
. 另一方面當 S 是一個有限集合時, K(S)/K 也未必是
finite extension, 除非 S 中的元素都是 algebraic over K.
我們有以下有關 finite extension 的充要條件.
![]() {1,..., n} 我們令
Fi = K(a1,..., ai). 由於
L = K(a1,..., an) = Fn 以及
Fi
{1,..., n} 我們令
Fi = K(a1,..., ai). 由於
L = K(a1,..., an) = Fn 以及
Fi ![]() Fi + 1, 利用 Lemma
1.2.3 我們有
Fi + 1, 利用 Lemma
1.2.3 我們有
![]() L 但
a
L 但
a ![]() K. 由於
[L : K] = [L : K(a)][K(a) : K], 馬上得知
[L : K(a)] < m
(因
a
K. 由於
[L : K] = [L : K(a)][K(a) : K], 馬上得知
[L : K(a)] < m
(因
a ![]() K, 故
[K(a) : K] > 1) 故由 induction 的假設知存在一個
finite set S' 使得
L = K(a)(S'). 故令
S = S'
K, 故
[K(a) : K] > 1) 故由 induction 的假設知存在一個
finite set S' 使得
L = K(a)(S'). 故令
S = S' ![]() {a}, 則知 S
是一個 finite set 且 L = K(S). 這裡 S 中的元素必定會 algebraic
over K, 這是因為 L/K 是 finite extension 所以 L 中的元素必皆
algebraic over K.
{a}, 則知 S
是一個 finite set 且 L = K(S). 這裡 S 中的元素必定會 algebraic
over K, 這是因為 L/K 是 finite extension 所以 L 中的元素必皆
algebraic over K.
![]()
![]() K[a1,..., an]
K[a1,..., an] ![]() L, 我們知
K[a1,..., an] 是 L over
K 的 subspace, 故知
dimK(K[a1,..., an])
L, 我們知
K[a1,..., an] 是 L over
K 的 subspace, 故知
dimK(K[a1,..., an])![]() [L : K]
因此由大學基礎代數講義Theorem 9.3.7 馬上就知
K[a1,..., an] 是一個
field, 故知
K[a1,..., an] = L. 這裡我們想用 induction 來證明,
讓大家更清楚這個結果.
[L : K]
因此由大學基礎代數講義Theorem 9.3.7 馬上就知
K[a1,..., an] 是一個
field, 故知
K[a1,..., an] = L. 這裡我們想用 induction 來證明,
讓大家更清楚這個結果.
![]() K[x] 皆有
f (a)
K[x] 皆有
f (a)![]() 0. 由於 K(a) 是一個包含 K 和 a 的 field, 對任意
f (x)
0. 由於 K(a) 是一個包含 K 和 a 的 field, 對任意
f (x) ![]() K[x], f (a) 當然也在 K(a) 中. 事實上
K[x], f (a) 當然也在 K(a) 中. 事實上
![]() K[x1,..., xn],
這種形式來表示. 但是要描述 L 中的元素, 我們仍可用
f (a1,..., an)/g(a1,..., an), 其中
f (x1,..., xn), g(x1,..., xn)
K[x1,..., xn],
這種形式來表示. 但是要描述 L 中的元素, 我們仍可用
f (a1,..., an)/g(a1,..., an), 其中
f (x1,..., xn), g(x1,..., xn) ![]() K[x1,..., xn] 且
g(a1,..., an)
K[x1,..., xn] 且
g(a1,..., an)![]() 0
來表示. 在本講義中我們僅探討 finite extension, 所以對於
transcendental extension 我們僅探討到此.
0
來表示. 在本講義中我們僅探討 finite extension, 所以對於
transcendental extension 我們僅探討到此.