

下一頁: The alternating group
上一頁: The Symmetric Group
前一頁: 一些 cycles 的運算
因為 Sn 中的元素可以看成將
{1,..., n} 的元素做排列組合,
Sn 中的元素稱之為一個 permutation. 一個 permutation
應該是可以用每次只將
{1,..., n} 中某兩個元素互換的方式組合得到.
將
{1..., n} 中的某兩個元素互換的這個動作我們稱之為 transposition. 其實它只是 Sn 中的一個 2-cycle 罷了.
為了方便起見, 在這兒我們還是用 2-cycle 這個稱呼.
前面提到每個 permutation 可以用一些 transposition 組合而成,
這用數學的方法表達就是如下:
証 明.
因為

可以寫成一些 cycles 的乘積, 要證明

可以寫成
2-cycles 的乘積, 我們只要證明每一個 cycle 都可寫成 2-cycles
的乘積即可. 事實上由式子 (
3.7) 知
(
a1 a3)(
a1 a2) = (
a1 a2 a3),
如此一直下去可之任意的
k-cycle
(
a1 a2 ... ak - 1 ak) 可寫成
(a1 a2 ... ak - 1 ak) = (a1 ak)(a1 ak - 1) ... (a1 a2).

這裡要注意: Lemma 3.4.14 並沒有說每一個 Sn
的元素都可以寫成 `disjoint' 2-cycle 的乘積. 事實上這是不對的, 如
(1 2 3) 就沒法子寫成 disjoint 2-cycle 的乘積.
你知道為什麼嗎? 其實很簡單: 因為若
(1 2 3) 是一些 disjoint
2-cycle 的乘積, 則利用 Proposition 3.4.9 知其 order 應該為
2, 不過
(1 2 3) 的 order 是 3 故一定不可能寫成 disjoint
2-cycle 的乘積. 另外 Lemma 3.4.14 也沒有提及寫成 2-cycle
的乘積寫法會唯一, 因為這也是錯的. 例如
(1 2 3) = (1 3)(1 2) = (1 2)(2 3)
其實連可寫成多少個 2-cycle 的乘積都不一定. 例如 (1 2) 這一個
2-cycle 就可以寫成
(1 3)(2 3)(1 3) 這三個 2-cycle
的乘積.
從上面這個觀點來看, 將一個 Sn 的元素寫成 2-cycle
的乘積好像沒什麼好處. 事實上在大學的代數中我們學 2-cycle
decomposition 只是為了方便去定義什麼是 even permutation 和 odd
permutation 罷了. 我們稱 Sn 中的元素是 even 如果它可以寫成偶數個
2-cycle 的乘積, 反之則稱為 odd.
你應該會覺得這個定義有點奇怪吧! 前面提過一個 Sn
的元素可以寫成多少個 2-cycle 的乘積是不一定的.
有沒有可能它一下可寫成偶數個乘積, 而又可以寫成奇數個呢?
下一個定理告訴我們這是不可能的.
Theorem 3.4.15
若

 Sn
Sn 且

=
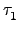 .
. 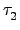 ...
... 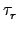
=
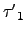 .
. 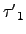 ...
... 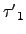
,
其中
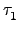
,...,
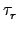
和
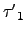
,...,
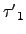
都是
2-cycles. 則
r 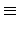 s
s(mod 2) (即
r 和
s 同奇同偶 : 2 |
r -
s).
証 明.
我們利用大家都學過的線性代數裡有關行列式的性質來證明此定理.
回顧一下: 給定一
n×
n 的矩陣
A, 如果將
A
中的某兩列互換所得的矩陣
A', 其行列式 det(
A') 會等於
-det(
A).
現在任取

 Sn 我們定義
Sn 我們定義  *A 這個矩陣是將 A 的第
i 列換到第
*A 這個矩陣是將 A 的第
i 列換到第  (i) 列. 例如若
(i) 列. 例如若
 = (i j) 則
= (i j) 則  *A
就是將 A 的第 i 列換到第 j 列, 且將第 j 列換到第 i 列,
換句話說若
*A
就是將 A 的第 i 列換到第 j 列, 且將第 j 列換到第 i 列,
換句話說若  是一個 2 cycle 則
是一個 2 cycle 則  *A 就是如上述將 A
的某兩列互換. 若
*A 就是如上述將 A
的某兩列互換. 若
 ,
,
 Sn, 則
(
Sn, 則
( .
.  )*A
是將 A 的第 i 列換到第
(
)*A
是將 A 的第 i 列換到第
( .
.  )(i) =
)(i) =  (
( (i))
列. 而
(i))
列. 而  *A 的第
*A 的第  (i) 列是 A 的第 i 列 且
(i) 列是 A 的第 i 列 且
 *(
*( *A) 是將
*A) 是將  *A 的第
*A 的第  (i) 列換到第
(i) 列換到第
 (
( (i)) 列. 換句話說
(i)) 列. 換句話說
 *(
*( *A) 是將 A 的第 i
列換到第
*A) 是將 A 的第 i
列換到第
 (
( (i)) 列. 這和
(
(i)) 列. 這和
( .
.  )*A 是一樣的,
所以我們有
)*A 是一樣的,
所以我們有
( . .  )*A = )*A =  *( *( *A) *A) 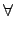  , ,  Sn. Sn. |
(3.10) |
現在若
 =
= 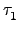 .
. 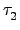 ...
... 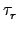 =
= 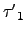 .
. 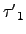 ...
... 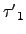 ,
考慮
,
考慮
 *In, 其中 In 是 n×n 的單位矩陣. 則由式子
(3.10) 知
*In, 其中 In 是 n×n 的單位矩陣. 則由式子
(3.10) 知

*
In =
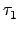
*(
... *(
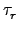
*
In)) =
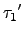
*(
... *(
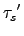
*
In)).
然而
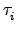
,
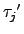
是 2-cycles, 它們每作用一次行列式值會變號,
所以得
det(

*
In) = (- 1)
r = (- 1)
s.
也就是說
r -
s
是一個偶數.

Theorem 3.4.15 告訴我們如果你找到偶數個 2-cycles 將  寫成這些 2-cycle 的乘積, 則
寫成這些 2-cycle 的乘積, 則  就不可能寫成奇數個 2-cycle
的乘積. 反之亦然. 因此我們有下面這個正式的定義:
就不可能寫成奇數個 2-cycle
的乘積. 反之亦然. 因此我們有下面這個正式的定義:
Definition 3.4.16
若

 Sn
Sn 可寫成偶數個 2-cycles 的乘積, 則稱

為一個
even permutation. 反之, 若

可寫成奇數個 2-cycles
的乘積, 則稱

為一個
odd permutation
在 Lemma 3.4.14 的證明中我們曾證得一個 k-cycle 可以寫成
k - 1 個 2-cycle 的乘積, 因此一個 k-cycle 是 even 若 k 是奇數.
反之, 若 k 是偶數則此 k-cycle 就是 odd 了. 另外若  可寫成 r 個 2-cycles 的乘積, 而
可寫成 r 個 2-cycles 的乘積, 而  可寫成 s 個 2-cycles
的乘積, 則
可寫成 s 個 2-cycles
的乘積, 則
 .
.  可寫成 r + s 個 2-cycles 的乘積.
因此我們有下一個結果:
可寫成 r + s 個 2-cycles 的乘積.
因此我們有下一個結果:
利用 Lemma 3.4.17 若將一個 Sn 的元素寫成 disjoint cycle
decomposition, 就可以很快的判斷其為 even 或 odd. 這也是寫成
disjoint cycle decomposition 的另一個好處.


下一頁: The alternating group
上一頁: The Symmetric Group
前一頁: 一些 cycles 的運算
Administrator
2005-06-18
![]()
![]() Sn 我們定義
Sn 我們定義 ![]() *A 這個矩陣是將 A 的第
i 列換到第
*A 這個矩陣是將 A 的第
i 列換到第 ![]() (i) 列. 例如若
(i) 列. 例如若
![]() = (i j) 則
= (i j) 則 ![]() *A
就是將 A 的第 i 列換到第 j 列, 且將第 j 列換到第 i 列,
換句話說若
*A
就是將 A 的第 i 列換到第 j 列, 且將第 j 列換到第 i 列,
換句話說若 ![]() 是一個 2 cycle 則
是一個 2 cycle 則 ![]() *A 就是如上述將 A
的某兩列互換. 若
*A 就是如上述將 A
的某兩列互換. 若
![]() ,
,![]()
![]() Sn, 則
(
Sn, 則
(![]() .
. ![]() )*A
是將 A 的第 i 列換到第
(
)*A
是將 A 的第 i 列換到第
(![]() .
. ![]() )(i) =
)(i) = ![]() (
(![]() (i))
列. 而
(i))
列. 而 ![]() *A 的第
*A 的第 ![]() (i) 列是 A 的第 i 列 且
(i) 列是 A 的第 i 列 且
![]() *(
*(![]() *A) 是將
*A) 是將 ![]() *A 的第
*A 的第 ![]() (i) 列換到第
(i) 列換到第
![]() (
(![]() (i)) 列. 換句話說
(i)) 列. 換句話說
![]() *(
*(![]() *A) 是將 A 的第 i
列換到第
*A) 是將 A 的第 i
列換到第
![]() (
(![]() (i)) 列. 這和
(
(i)) 列. 這和
(![]() .
. ![]() )*A 是一樣的,
所以我們有
)*A 是一樣的,
所以我們有 ![]() =
= ![]() .
. ![]() ...
... ![]() =
= ![]() .
. ![]() ...
... ![]() ,
考慮
,
考慮
![]() *In, 其中 In 是 n×n 的單位矩陣. 則由式子
(3.10) 知
*In, 其中 In 是 n×n 的單位矩陣. 則由式子
(3.10) 知
![]() 寫成這些 2-cycle 的乘積, 則
寫成這些 2-cycle 的乘積, 則 ![]() 就不可能寫成奇數個 2-cycle
的乘積. 反之亦然. 因此我們有下面這個正式的定義:
就不可能寫成奇數個 2-cycle
的乘積. 反之亦然. 因此我們有下面這個正式的定義: