


下一頁: Sn 的 normal subgroup
上一頁: The Symmetric Group
前一頁: Even and odd permutations
在 Sn 中的 even permutations 所成的集合形成一個 group 稱之為
alternating group.
Theorem 3.4.18
令
An 是
Sn 中所有的 even permutation 所成的集合.
- An 是 Sn 的一個 normal subgroup.
-
|
An| =
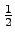 n .
n . (
n - 1)
... 2
. 1 =
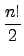
.
証 明.
考慮
sgn :
Sn
{1, - 1} 這個函數其中
若將 {1, - 1} 看成是一個乘法群, 則 1 是其 identity, 且
Lemma
3.4.17 告訴我們
sgn 是一個 group homomorphism. 由定義知
ker(sgn) =
An, 故由 Lemma
2.5.4 知
An 是
Sn 的一個
normal subgroup. 又任意的 2-cycle 是 odd, 故知
sgn 是 onto,
所以由 First Isomorphism 定理 (Corollary
2.6.2) 知
Sn/
An 
{1, - 1}. 也就是說
|
An| = |
Sn|/2.

Definition 3.4.19
我們將 Sn 中所有的 even permutation 所成的集合定為 An 稱之為
the alternating group of degree n.
Remark 3.4.20
由於 An 的個數是 Sn 的一半, 那麼令一半當然是 Sn 中的 odd
permutations 了, 所以在 Sn 中 odd permutation 和 even permutation
的個數一樣多.
每一個 Sn 的元素可以寫成一些 2-cycle 的乘積 (Lemma
3.4.14). 那麼 An 的元素都可以有甚麼特殊的表示法嗎?
証 明.
因

 An
An 故存在 2
r 個 2-cycles
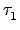
,...,
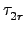
使得

=
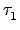 .
. 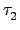 ...
... 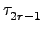 .
. 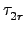
.
我們將這些
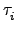
兩個兩個先擺一起, 也就是考慮

= (
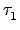 .
. 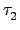
)
... (
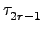 .
. 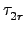
).
若能證明任兩個 2-cycle 相乘都能寫成一些 3-cycles 的乘積,
那麼證明就完成了.
考慮
 = (a b),
= (a b),
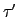 = (c d ) 是 Sn 中兩個 2-cycle.
有三種可能情況:
= (c d ) 是 Sn 中兩個 2-cycle.
有三種可能情況:
(1)
{a, b} = {c, d}, 此時
 .
. 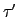 是 identity,
所以我們可以將
是 identity,
所以我們可以將
 .
. 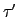 寫成
寫成
(1 2 3)(3 2 1)
(2) {a, b} 和 {c, d} 中恰有一數相同, 不失一般性我們假設 a = c
但 b d. 此時由式子 (3.7) 知
d. 此時由式子 (3.7) 知
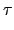 .
. 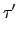
= (
a b)(
a d )= (
a d b)
(3) {a, b} 和 {c, d} 皆相異, 此時我們有
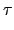 .
. 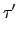
= (
a b)(
c d )= (
a d b)(
a d c)

因為 3-cycle 是 even permutation, 所以所有的 3-cycles 都在 An
中. 下一個定理告訴我們反過來也是對的.
Proposition 3.4.22
若
H 是
Sn 的一個 nontrivial proper subgroup, 假如
H
中含有所有的 3-cycles, 則
H =
An.
証 明.
若

 An
An, 則由 Lemma
3.4.21 知存在 3-cycles,
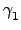
,...,
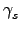
使得

=
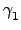 ...
... 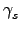
.
由假設, 這些
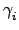
都在
H 中. 又因
H 是 group, 由封閉性知
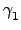 ...
... 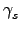
 H
H. 也就是說

 H
H. 故得
An  H
H. 然而
H Sn
Sn 故
|
H| <
n! = 2|
An| 再由 Lagrange
定理 (Theorem
2.2.2) 知 |
H| 是 |
An| 的倍數. 唯一的可能就是
|
H| = |
An|. 故得
H =
An 



下一頁: Sn 的 normal subgroup
上一頁: The Symmetric Group
前一頁: Even and odd permutations
Administrator
2005-06-18
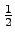 n . (n - 1) ... 2 . 1 =
n . (n - 1) ... 2 . 1 = 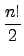 .
.

![]() = (a b),
= (a b),
![]() = (c d ) 是 Sn 中兩個 2-cycle.
有三種可能情況:
= (c d ) 是 Sn 中兩個 2-cycle.
有三種可能情況:
![]() .
. ![]() 是 identity,
所以我們可以將
是 identity,
所以我們可以將
![]() .
. ![]() 寫成
寫成
![]() d. 此時由式子 (3.7) 知
d. 此時由式子 (3.7) 知