


下一頁: An 的 normal subgroup
上一頁: The Symmetric Group
前一頁: The alternating group
我們將介紹當 n 5 時 An 是 Sn 中唯一的 nontrivial normal
subgroup.
5 時 An 是 Sn 中唯一的 nontrivial normal
subgroup.
因 S3 只有 6 個元素, 我們將它們一一列出, 記有: (1 2),
(1 3), (2 3),
(1 2 3),
(1 3 2) 和
identity. 其中 A3 就是由
(1 2 3) 所產生的 cyclic group.
其他的 2-cycle 都只生成 order 2 的 subgroup. 考慮 (1 2)
所生成的 cyclic group
 (1 2)
(1 2) , 由於
, 由於
(1 3)(1 2)(1 3) = (3 2)
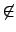
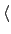
(1 2)
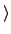
 (1 2)
(1 2) 不是 S3 的 normal subgroup.
同理知其他 order 為 2 的 subgroup 皆不是 normal. 因此在 S3
中只有一個 nontrivial normal subgroup, 就是 A3.
不是 S3 的 normal subgroup.
同理知其他 order 為 2 的 subgroup 皆不是 normal. 因此在 S3
中只有一個 nontrivial normal subgroup, 就是 A3.
在 S4 中情況就不一樣了. 除了 A4 外 還有一個 normal subgroup
N = {I,(1 2)(3 4),(1 3)(2 4),(1 4)(2 3)}.
很容易看出 N 中除了 identity 以外, 每個元素都是 order 2,
也就是自己是自己的 inverse. 我們來檢查 N 是乘法封閉的. 由
(1 2)(3 4) . (1 3)(2 4) = (1 4)(2 3)
就可以知
N 是乘法封閉的, 由此知 N 是 S4 的 subgroup. (由於 N
中的元素都是 even permutation 可知 N 也是 A4 的 subgroup.)
仔細觀察 N 中除了 identity 外其他的元素都是兩個 disjoint 2-cycle
相乘. 而且在 S4 中所有可能的兩個 disjoint 2-cycle 相乘的
permutation 都在 N 中. 若
 = (a b)(c d ) 是兩個
disjoint 2-cycle 相乘, 則由 Lemma 3.4.10 知對任意的
= (a b)(c d ) 是兩個
disjoint 2-cycle 相乘, 則由 Lemma 3.4.10 知對任意的

 S4,
S4,
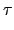 .
. 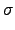 .
. 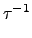
= (
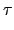
(
a)
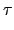
(
b))(
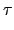
(
c)
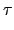
(
d ))
也是由兩個 disjoint 2-cycle 相乘的 permutation. 換言知, 若

 N, 則對任意的
N, 則對任意的

 S4 皆得
S4 皆得
 .
.  .
. 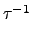
 N, 故 N 是 S4 的 normal
subgroup.
N, 故 N 是 S4 的 normal
subgroup.
當 n 5 時, 由於 Sn 的 order 已很大,
我們不可能如前面的方式討論下去. 我們有一個很重要的 Lemma
可以幫我們處理一般的狀況.
5 時, 由於 Sn 的 order 已很大,
我們不可能如前面的方式討論下去. 我們有一個很重要的 Lemma
可以幫我們處理一般的狀況.
Lemma 3.4.23
若
N 是
Sn 的一個 nontrivial proper normal subgroup, 且
N
中存在一個 3-cycle, 則
N =
An.
証 明.
Proposition
3.4.22, 告訴我們要證明
N =
An, 只要證明所有的
3-cycle 皆在
N 中就可. 因此若
(
a b c) 是
N 中的一個
3-cycle, 我們想利用
N 是 normal 的性質證明任意的 3-cycle
(
a' b' c') 也在
N 中.
由於 N 在 Sn 中 normal, 對任意的

 Sn, 因為
(a b c)
Sn, 因為
(a b c)  N, 故有
N, 故有
 . (a b c) .
. (a b c) . 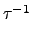
 N. 然而由 Lemma 3.4.10 知
N. 然而由 Lemma 3.4.10 知
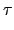 .
. (
a b c)
. 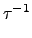
= (
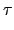
(
a)
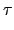
(
b)
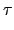
(
c)).
因此對任意的 3-cycle
(
a' b' c'), 我們只要在
Sn 找到一個

滿足

(
a) =
a',

(
b) =
b' 和

(
c) =
c' 即可.
這當然做得到, 因為
a,
b,
c 皆相異, 而
a',
b',
c' 也都相異,
我們當然可找到一個 1-1 的函數將
a 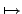 a'
a',
b 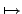 b'
b',
c 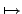 c'
c'. 也就是說對任意的 3-cycle
(
a' b' c'),
我們都可以在
Sn 找到一個

滿足
 .
. (
a b c)
. 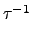
= (
a' b' c'). 所以由
 .
. (
a b c)
. 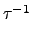
 N
N 得
(
a' b' c')
 N
N.

綜合一下我們所知的結果: Lemma 3.4.22 告訴我們若已知 H 是
Sn 的一個 nontrivial proper subgroup, 則要證明 H = An
須證明所有 Sn 的 3-cycle 都在 H 中才行; 然而若已知 H 是 normal 那麼 Lemma 3.4.23 告訴我們只要在 H 中找到一個 3-cycle 就可得
H = An.
現在我們可以證明當 n 5 時 An 是 Sn 唯一的 nontrivial
normal subgroup.
5 時 An 是 Sn 唯一的 nontrivial
normal subgroup.
Theorem 3.4.24
當
n
5 時, 若
N 是
Sn 的 nontrivial proper normal
subgroup, 則
N =
An.
証 明.
由 Lemma
3.4.23 知我們只要想辦法在
N 中找到一個 3-cycle,
就可得
N =
An.
現因 N 是 nontrivial, 所以 N 不是 identity. 換句話說在 N
中存在一個  不是 identity. 既然
不是 identity. 既然  不是 identity, 那麼
不是 identity, 那麼
 必將
{1 ..., n} 中某一整數 a 送到另一數 b, 即
必將
{1 ..., n} 中某一整數 a 送到另一數 b, 即
 (a) = b
(a) = b a.
a.  是我們在 N 中隨便挑的非 identity
的元素, 它長怎樣我們一點都不清楚. 它有可能將 b 送回到 a
也有可能送到另一個數 a', 所以我們可分成以下兩個 cases:
是我們在 N 中隨便挑的非 identity
的元素, 它長怎樣我們一點都不清楚. 它有可能將 b 送回到 a
也有可能送到另一個數 a', 所以我們可分成以下兩個 cases:
-
 (a) = b, 且
(a) = b, 且
 (b) = a;
(b) = a;
-
 (a) = b 但
(a) = b 但
 (b) = a'
(b) = a' a.
a.
我們接下來想利用
N normal 和利用

這個微弱的訊息來幫我們在
N 中找到更具體一點的元素. 我們的方法是這樣的: 試著在
Sn
中找到一個 2-cycle

, 使得
 .
.  .
. 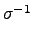


. 如此一來
(
 .
.  .
. 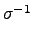
)
. 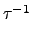
就不會是 identity.
然而
由

 N
N, 得
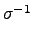
 N
N 再利用
N 是 normal 知
 .
. 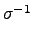 .
. 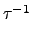
 N
N. 因此
 .
. (
 .
. 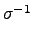 .
. 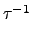
)
 N
N.
也就是我們又在
N 中找到一個新的不是 identity 的元素.
當  是 case 1 時, 我們在
{1,..., n} 中找另一個數 c,
使得 c
是 case 1 時, 我們在
{1,..., n} 中找另一個數 c,
使得 c a 且 c
a 且 c b. 令
b. 令
 = (a c). 則由 Lemma
3.4.10 知
= (a c). 則由 Lemma
3.4.10 知
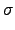 .
. 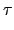 .
. 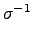
= (
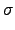
(
a)
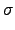
(
c)) = (
b 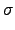
(
c)).
注意此時因

(
b) =
a 但
c b
b 故知

(
c)
 a
a. 也就是說
當  是 case 2 時, 我們只要考慮
是 case 2 時, 我們只要考慮
 = (a b) 就可.
因為此時
= (a b) 就可.
因為此時
 (b) = a'
(b) = a' a, 故
a, 故
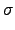 .
. 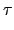 .
. 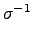
= (
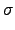
(
a)
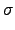
(
b)) = (
b a')
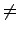
(
a b) =
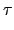
.
綜合以上 cases 1 和 2, 我們知: 不管  為何我們都可以在 Sn
中找到一個 2-cycle
為何我們都可以在 Sn
中找到一個 2-cycle  使得
使得
且不是 identity.
更重要的是

=
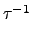
和
 .
.  .
. 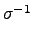
都是 2-cycles. 也就是在
N 中存在一個元素
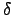
是兩個
2-cycle 相乘且不是 identity.
這個 N 中的元素 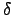 有可能是以下兩種情況:
有可能是以下兩種情況:
- 甲
-
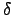 = (i j)(j k), 其中 i, j, k 皆相異.
= (i j)(j k), 其中 i, j, k 皆相異.
- 乙
-
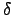 = (i j)(k l ), 其中 i, j, k, l 皆相異.
= (i j)(k l ), 其中 i, j, k, l 皆相異.
若是 case 甲, 則
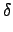
= (
i j)(
j k) = (
i j k)
 N
N,
故知
N 中有一個 3-cycle.
若是 case 乙, 我們選一個在
{1,..., n} 中但在
{i, j, k, l}
以外的元素 m (這就是為何此定理需假設 n 5 的原因). 令
5 的原因). 令
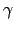 = (i m), 則因
= (i m), 則因
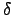
 N 且 N 是 normal, 知
N 且 N 是 normal, 知
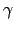 .
. 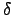 .
. 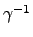 = (m j)(k l )
= (m j)(k l )  N. 再由
N. 再由
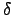
 N 知
N 知
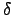 . (
. (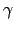 .
. 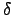 .
. 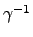 )
)  N. 然而
N. 然而
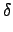 . ( . (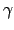 . . 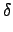 . . 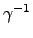 ) ) |
= |
(i j)(k l )(m j)(k l ) |
|
| |
= |
(i j)(m j) |
|
| |
= |
(i j m) |
|
故知
N 中有一個 3-cycle.
我們證明了在任何狀況下 N 中皆有一個 3-cycle, 故得 N = An.

記得我們在 S4 中找到一個不是 A4 的 normal subgroup, 它是由一些
兩個 disjoint 2-cycle 相乘的 permutation 所形成.
當初我們證這些元素相乘有封閉性, 不過在 Theorem 3.4.24 的證明
(case 乙) 我們證得在 n 5 時這類元素相乘不再封閉.
5 時這類元素相乘不再封閉.



下一頁: An 的 normal subgroup
上一頁: The Symmetric Group
前一頁: The alternating group
Administrator
2005-06-18
![]() (1 2)
(1 2)![]() , 由於
, 由於
![]() 5 時, 由於 Sn 的 order 已很大,
我們不可能如前面的方式討論下去. 我們有一個很重要的 Lemma
可以幫我們處理一般的狀況.
5 時, 由於 Sn 的 order 已很大,
我們不可能如前面的方式討論下去. 我們有一個很重要的 Lemma
可以幫我們處理一般的狀況.
![]()
![]() Sn, 因為
(a b c)
Sn, 因為
(a b c) ![]() N, 故有
N, 故有
![]() . (a b c) .
. (a b c) . ![]()
![]() N. 然而由 Lemma 3.4.10 知
N. 然而由 Lemma 3.4.10 知
![]() 5 時 An 是 Sn 唯一的 nontrivial
normal subgroup.
5 時 An 是 Sn 唯一的 nontrivial
normal subgroup.
![]() 不是 identity. 既然
不是 identity. 既然 ![]() 不是 identity, 那麼
不是 identity, 那麼
![]() 必將
{1 ..., n} 中某一整數 a 送到另一數 b, 即
必將
{1 ..., n} 中某一整數 a 送到另一數 b, 即
![]() (a) = b
(a) = b![]() a.
a. ![]() 是我們在 N 中隨便挑的非 identity
的元素, 它長怎樣我們一點都不清楚. 它有可能將 b 送回到 a
也有可能送到另一個數 a', 所以我們可分成以下兩個 cases:
是我們在 N 中隨便挑的非 identity
的元素, 它長怎樣我們一點都不清楚. 它有可能將 b 送回到 a
也有可能送到另一個數 a', 所以我們可分成以下兩個 cases:
![]() 是 case 1 時, 我們在
{1,..., n} 中找另一個數 c,
使得 c
是 case 1 時, 我們在
{1,..., n} 中找另一個數 c,
使得 c![]() a 且 c
a 且 c![]() b. 令
b. 令
![]() = (a c). 則由 Lemma
3.4.10 知
= (a c). 則由 Lemma
3.4.10 知
![]() 是 case 2 時, 我們只要考慮
是 case 2 時, 我們只要考慮
![]() = (a b) 就可.
因為此時
= (a b) 就可.
因為此時
![]() (b) = a'
(b) = a'![]() a, 故
a, 故
![]() 為何我們都可以在 Sn
中找到一個 2-cycle
為何我們都可以在 Sn
中找到一個 2-cycle ![]() 使得
使得
![]() 有可能是以下兩種情況:
有可能是以下兩種情況:
![]() 5 的原因). 令
5 的原因). 令
![]() = (i m), 則因
= (i m), 則因
![]()
![]() N 且 N 是 normal, 知
N 且 N 是 normal, 知
![]() .
. ![]() .
. ![]() = (m j)(k l )
= (m j)(k l ) ![]() N. 再由
N. 再由
![]()
![]() N 知
N 知
![]() . (
. (![]() .
. ![]() .
. ![]() )
) ![]() N. 然而
N. 然而 ![]()
![]() 5 時這類元素相乘不再封閉.
5 時這類元素相乘不再封閉.