


下一頁: Disjoint cycle decomposition
上一頁: The Symmetric Group
前一頁: The group A(S) and
前面提過 A(S) 這一個 group 只和 S 的元素個數有關. 今若 S 有
n 個元素, 那麼我們不妨考慮
S = {1, 2,..., n} 這一個集合.
此時我們將 A(S) 也就是從
{1, 2,..., n} 到
{1, 2,..., n}
所有 1-1 且 onto 的函數所成的集合特別記做 Sn, 稱之為 the symmetric group of degree n. Cayley's Theorem 告訴我們所有 order
為 n 的 group 都會 isomorphic 到 Sn 的某一個 subgroup, 所以研究
Sn 顯得特別重要.
從
{1, 2,..., n} 到
{1, 2,..., n} 所有 1-1 且 onto
的函數到底有多少個呢? 相信大家在高中都已學過了. 先考慮 1
可以送到什麼? 結果有 n 種選擇, 不過因 1 已選擇去哪個數了,
因要求一對一, 2 只剩下 n - 1 個選擇. 由此繼續下去我們得知 Sn 的
order.
一般談 Sn 我們是不談 n = 1 和 n = 2 的狀況: 因 S1
只有一個元素, 所以只有 identity. 而 S2 只有 2 個元素, 一定是
cyclic. 所以我們以後只談 n 3 的狀況.
3 的狀況.
要討論 Sn 我們當然要想個法子將其元素表示出來. 例如在 S5 中若
 是將
1
是將
1 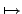 2,
2
2,
2 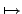 3,
3
3,
3 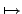 1,
4
1,
4 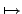 5
及
5
5
及
5 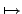 4, 則我們可以用
4, 則我們可以用
來表示. 而
表示  將
1
將
1 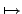 3,
2
3,
2 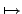 4,
3
4,
3 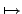 5,
4
5,
4 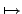 1 且
5
1 且
5 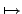 2. 那麼
2. 那麼
 o
o 是甚麼呢?
因為
是甚麼呢?
因為  將
1
將
1 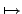 3, 而
3, 而  將
3
將
3 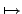 1
所以合成起來得
1
所以合成起來得
 o
o 將
1
將
1 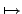 1. 而
1. 而  將
2
將
2 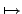 4,
4,  將
4
將
4 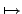 5 故
5 故
 o
o 將
2
將
2 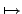 5. 同理一個一個計算下去我們可得
5. 同理一個一個計算下去我們可得
同理考慮
 o
o 可得
可得
由式子 (3.3) 和 (3.4) 知
 o
o

 o
o 所以 S5 不是 abelian.
事實上對於所有的 n
所以 S5 不是 abelian.
事實上對於所有的 n 3, Sn 都不是 abelian.
3, Sn 都不是 abelian.
當
 ,
,
 Sn, 由於
Sn, 由於  ,
,  都是函數,
其乘法就是函數的合成. 為了方便起見以後我們不再用
都是函數,
其乘法就是函數的合成. 為了方便起見以後我們不再用
 o
o 表示其合成而用
表示其合成而用
 .
.  取代.
取代.



下一頁: Disjoint cycle decomposition
上一頁: The Symmetric Group
前一頁: The group A(S) and
Administrator
2005-06-18
![]() 3 的狀況.
3 的狀況.
![]() 是將
1
是將
1 ![]() 2,
2
2,
2 ![]() 3,
3
3,
3 ![]() 1,
4
1,
4 ![]() 5
及
5
5
及
5 ![]() 4, 則我們可以用
4, 則我們可以用 ![]() ,
,![]()
![]() Sn, 由於
Sn, 由於 ![]() ,
, ![]() 都是函數,
其乘法就是函數的合成. 為了方便起見以後我們不再用
都是函數,
其乘法就是函數的合成. 為了方便起見以後我們不再用
![]() o
o![]() 表示其合成而用
表示其合成而用
![]() .
. ![]() 取代.
取代.