

下一頁: Disjoint cycle 的性質
上一頁: The Symmetric Group
前一頁: The symmetric group of
用如式子 (3.1) 的方法表示 Sn 的元素有時稍嫌麻煩.
我們介紹一個簡便的表示法. 這個方法稱為 cycle 表示法. 它不只使用簡便,
而且許多 Sn 的性質都可利用這方法簡單求得. 可以說是相當的重要.
Definition 3.4.3
令
i1,
i2...,
ik 是在
{1, 2,...,
n} 中
k 個相異整數.
我們用
(i1 i2 ... ik)
表示
Sn 中的一個元素

將
s 
{1, 2,...,
n} 送到
換句話說

將
i1  i2
i2,
i2  i3
i3,
...,
ik - 1  ik
ik, 而將
ik 送回
i1, 而將
i1,...,
ik 以外的元素原封不動.
我們稱
(i1 i2 ... ik) 是一個 k-cycle.
例如在 S5 中我們有以下的等式:
一個 cycle 是 Sn 中的元素, 反之任一 Sn 中的元素未必是一個
cycle. 不過它們都可寫成一些 cycle 的乘積 (別忘了這裡指的是合成).
我們就用式子 (3.1) 當例子來將  用 cycle 表示出來. 因
用 cycle 表示出來. 因
 將
1
將
1  2 所以我們先寫下
2 所以我們先寫下
(1 2
接著  將
2
將
2  3 所以繼續寫下
3 所以繼續寫下
(1 2 3
然後  將
3
將
3  1 所以我們寫下
1 所以我們寫下
(1 2 3)
用 ``)'' 將 3 框住表示  將 3 送回 1.
這樣我們寫下了一個 3-cycle. 不過這
(1 2 3) 並不是
將 3 送回 1.
這樣我們寫下了一個 3-cycle. 不過這
(1 2 3) 並不是  ,
別忘了
,
別忘了  還將
4
還將
4  5 及
5
5 及
5  4. 所以需補上
(4 5) 這一個 cycle. 因此我們將式子 (3.1) 表成
4. 所以需補上
(4 5) 這一個 cycle. 因此我們將式子 (3.1) 表成

= (4 5)(1 2 3).
這裡其實我們是將
(1 2 3) 看成是 S5 中的
這一個元素, 而
所以將之相乘得  . 同法式子 (3.2) 中的
. 同法式子 (3.2) 中的  將
1
將
1  3, 故先寫下
3, 故先寫下
(1 3
接著  將
3
將
3  5
所以繼續寫下
5
所以繼續寫下
(1 3 5
而後  將
5
將
5  2, 故寫
2, 故寫
(1 3 5 2
接著  將
2
將
2  4, 所以寫下
4, 所以寫下
(1 3 5 2 4
最後  將 4 送回 1 故補上
``)'' 得
將 4 送回 1 故補上
``)'' 得

= (1 3 5 2 4).
注意此時每一個元素的動作都用這一個 cycle 表示出來了, 所以  是一個 5-cycle.
是一個 5-cycle.
接下來我們看
 .
. 
= (4 5)(1 2 3)(1 3 5 2 4)
會是甚麼? 當然了你可以將這些 cycles 還原成原來複雜的形式再計算,
不過這裡我們想直接用 cycle 的看法來處理. 首先觀察
(1 3 5 2 4) 將
1  3, 不過後面的
(1 2 3) 將
3
3, 不過後面的
(1 2 3) 將
3  1, 最後 (4 5) 固定 1 所以知
1, 最後 (4 5) 固定 1 所以知
 .
.  將
1
將
1  1. 也就是說在
1. 也就是說在
 .
.  的
cycle 寫法中 1 不會出現. 現在看 2:
(1 3 5 2 4) 將
2
的
cycle 寫法中 1 不會出現. 現在看 2:
(1 3 5 2 4) 將
2  4, 而後面的
(1 2 3) 將 4 固定住, 最後
(4 5) 將
4
4, 而後面的
(1 2 3) 將 4 固定住, 最後
(4 5) 將
4  5 故知
5 故知
 .
.  將
2
將
2  5,
所以我們寫下
5,
所以我們寫下
(2 5
然而
(1 3 5 2 4) 將
5  2, 而後面的
(1 2 3) 將
2
2, 而後面的
(1 2 3) 將
2  3, 最後 (4 5) 固定
3, 所以得
3, 最後 (4 5) 固定
3, 所以得
 .
.  將
5
將
5  3, 我們記下
3, 我們記下
(2 5 3
然而
(1 3 5 2 4) 將
3  5, 且
(1 2 3) 將 5 固定住, 最後 (4 5) 將
5
5, 且
(1 2 3) 將 5 固定住, 最後 (4 5) 將
5  4 故知
4 故知
 .
.  將
3
將
3  4, 所以繼續寫下
4, 所以繼續寫下
(2 5 3 4
最後
(1 3 5 2 4) 將
4  1, 而後面的
(1 2 3) 將
1
1, 而後面的
(1 2 3) 將
1  2, 然後 (4 5) 固定
2, 所以得
2, 然後 (4 5) 固定
2, 所以得
 .
.  將 4 送回了 2, 我們得知
將 4 送回了 2, 我們得知
 .
. 
= (2 5 3 4).
兩個 cycles
(i1 ... ik) 和
(j1 ... jl)
如果其中
{i1,..., ik}  {j1,..., jl} =
{j1,..., jl} = 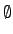 則稱此兩
cycle 為 disjoint cycles. 如果將 Sn 中的元素寫成一些兩兩
disjoint 的 cycles 的乘積 (當然包括只有一個 cycle 的情況),
我們就稱之為 disjoint cycle decomposition. 如前面
(4 5)(1 2 3) 和
(1 3 5 2 4) 就分別是
則稱此兩
cycle 為 disjoint cycles. 如果將 Sn 中的元素寫成一些兩兩
disjoint 的 cycles 的乘積 (當然包括只有一個 cycle 的情況),
我們就稱之為 disjoint cycle decomposition. 如前面
(4 5)(1 2 3) 和
(1 3 5 2 4) 就分別是
 和
和  的 disjoint cycle decomposition.
的 disjoint cycle decomposition.
我們簡單的說明一下對任意的

 Sn, 其 disjoint cycle
decomposition 是存在的. 作法就如同前面的例子, 任取一數
a1
Sn, 其 disjoint cycle
decomposition 是存在的. 作法就如同前面的例子, 任取一數
a1  {1,..., n} 我們先考慮
{1,..., n} 我們先考慮  將 a1 送到何處? 若
將 a1 送到何處? 若
 (a1) = a1, 則知 a1 不會出現在 cycle decomposition 之中,
所以我們繼續考慮其他的數. 如果
(a1) = a1, 則知 a1 不會出現在 cycle decomposition 之中,
所以我們繼續考慮其他的數. 如果
 (a1) = a2
(a1) = a2 a1 則寫下
a1 則寫下
(a1 a2
接下來看
 (a2) 為何? ...
如此繼續下去直到第一個 ak 使得
(a2) 為何? ...
如此繼續下去直到第一個 ak 使得
 (ak) 會和前面的某數相同.
也就是說
a1,..., ak 都相異但
(ak) 會和前面的某數相同.
也就是說
a1,..., ak 都相異但
 (ak)
(ak)  {a1,..., ak - 1}. 不過此時
{a1,..., ak - 1}. 不過此時
 (ak)
非得等於 a1 不可, 因為若
(ak)
非得等於 a1 不可, 因為若
 (ak) = ai, 其中 i > 1, 則已知
(ak) = ai, 其中 i > 1, 則已知
 (ai - 1) = ai, 由
(ai - 1) = ai, 由  是 1-1 知
ak = ai - 1 這和
a1,..., ak 兩兩相異矛盾, 所以得
是 1-1 知
ak = ai - 1 這和
a1,..., ak 兩兩相異矛盾, 所以得
 (ak) = a1.
也就是說我們得到一個 cycle:
(ak) = a1.
也就是說我們得到一個 cycle:
(a1 ... ak).
接下來我們考慮
{a1,..., ak} 以外的數 b1,
再利用同樣的方式得到一個 cycle. 如此繼續下去直到將所有
{1,..., n} 考慮完畢, 然後得  就是這些 cycles 的乘積.
當然了利用
就是這些 cycles 的乘積.
當然了利用  是 1-1 我們很容易看出這樣做出的 cycles 都是
disjoint.
是 1-1 我們很容易看出這樣做出的 cycles 都是
disjoint.
接下來我們要說 disjoint cycle decomposition 是唯一的.
不過這裡的唯一性要說明一下. 首先觀察
(1 2 3) 這一個 cycle
其實它和
(2 3 1) 及
(3 1 2) 都表示同一個函數: 即
1  2,
2
2,
2  3,
3
3,
3  1. 因此我們將之視為同一
cycle (不過要注意
(1 3 2) 是不同的 cycle). 另外
(1 2 3)(4 5) 和
(4 5)(1 2 3)
也是同一個函數所以我們也將之視為同樣的 decomposition.
1. 因此我們將之視為同一
cycle (不過要注意
(1 3 2) 是不同的 cycle). 另外
(1 2 3)(4 5) 和
(4 5)(1 2 3)
也是同一個函數所以我們也將之視為同樣的 decomposition.
Lemma 3.4.4
令

= (
a1 a2 ... ak) 和

= (
b1 b2 ... bl) 是
Sn 的兩個 cycles.
- 如果 k = l 且 a1 = b2, a2 = b3, ...,
ak - 1 = bk,
ak = b1, 則
 =
=  .
.
- 如果
 和
和  是 disjoint, 即
{a1,..., ak}
是 disjoint, 即
{a1,..., ak}  {b1,..., bl} =
{b1,..., bl} = 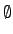 , 則
, 則
 .
.  =
=  .
.  .
.
証 明.
我們曾經強調過, 要說明兩個
Sn 中的元素是相同的只要將之視為函數,
將
{1,...,
n} 中任意數代入都相等就可.
(1) 若
x  {1,..., n} 但
x
{1,..., n} 但
x 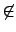 {a1,..., ak}, 則知
{a1,..., ak}, 則知
 (x) = x, 但由假設知
(x) = x, 但由假設知
{a1,..., ak} = {b1,..., bl},
所以
x 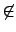
{
b1,...,
bl}, 也就是說

(
x) =
x.
若
x  {a1,..., ak}, 假設 x = ai,
1
{a1,..., ak}, 假設 x = ai,
1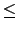 i
i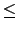 k - 2, 則
k - 2, 則

(
x) =

(
ai) =
ai + 1 =
bi + 2.
此時因
ai =
bi + 1, 所以

(
x) =

(
bi + 1) =
bi + 2.
而當
x =
ak - 1 時,

(
x) =

(
ak - 1) =
ak =
b1.
此時因
ak - 1 =
bk, 故

(
x) =

(
bk) =
b1.
最後當
x =
ak 時,

(
x) =

(
ak) =
a1 =
b2.
此時因
ak =
b1 所以

(
x) =

(
b1) =
b2.
得證對所有的
x 
{1,...,
n} 皆有

(
x) =

(
x), 因此知

=

.
(2) 此時由假設  和
和  是 disjoint, 所以
x
是 disjoint, 所以
x  {1,..., n} 可分成三種情況: (a)
x
{1,..., n} 可分成三種情況: (a)
x 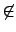 {a1,..., ak}
{a1,..., ak} 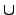 {b1,..., bl}; (b)
x
{b1,..., bl}; (b)
x  {a1,..., ak}; (c)
x
{a1,..., ak}; (c)
x  {b1,..., bl}.
{b1,..., bl}.
當 x 是屬狀況 (a) 時, 得
 (x) =
(x) =  (x) = x 故
(x) = x 故
(
 .
. 
)(
x) =

(

(
x)) =

(
x) =
x,
同理知
(
 .
. 
)(
x) =
x.
當 x 是屬狀況 (b) 時, 得
 (x)
(x)  {a1,..., ak} 但由
disjoint 知 x 和
{a1,..., ak} 但由
disjoint 知 x 和  (x) 皆不屬於
{b1,..., bl} 故
(x) 皆不屬於
{b1,..., bl} 故
 (x) = x 且
(x) = x 且
 (
( (x)) =
(x)) =  (x). 所以知
(x). 所以知
且
最後若
x
是屬狀況 (c) 時, 同狀況 (b) 可知
(
 .
. 
)(
x) =

(
x) = (
 .
. 
)(
x).
故得
 .
. 
=
 .
. 
.

Remark 3.4.5
在 Lemma
![[*]](crossref.gif)
中我們證得
(a1 a2 ... ak - 1 ak)
和
(ak a1 ... ak - 2 ak - 1)
為同一 cycle. 對
(
ak a1 ... ak - 2 ak - 1) 再套用一次 Lemma
![[*]](crossref.gif)
可得
(ak - 1 ak ... ak - 3 ak - 2)
也是同一 cycle.
如此一直循環下去我們可得到同一個
k-cycle 有
k 種寫法.
另外我們要強調的是若  和
和  不是 disjoint 時, 則
不是 disjoint 時, 則
 .
.  並不一定等於
並不一定等於
 .
.  (前面已給過例子了).
(前面已給過例子了).
現在我們可以說如果將 Lemma 3.4.4 的這兩種狀況忽略
(即不管一個 cycle 的循環或兩個 disjoint cycle 的順序), 那麼任一個
Sn 的元素寫成 disjoint cycle decomposition 的寫法唯一. 假設

 Sn 有兩種 disjoint cycle decompositions:
Sn 有兩種 disjoint cycle decompositions:
 =
= 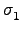 ...
... 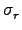 和
和
 =
= 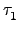 ...
... 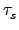 , 其中
, 其中
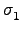 ,...,
,...,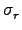 和
和
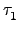 ,...,
,...,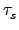 分別是兩組
disjoint cycles. 假設
a1
分別是兩組
disjoint cycles. 假設
a1  {1,..., n} 在
{1,..., n} 在 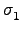 這個 cycle
出現, 而
這個 cycle
出現, 而
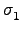 (a1) = a2, 則我們有
(a1) = a2, 則我們有
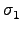
= (
a1 a2 ...
然而
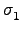 ,...,
,...,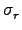 是
disjoint 所以 a1, a2 不會在
是
disjoint 所以 a1, a2 不會在
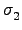 ,...,
,...,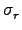 中出現;
也就是說當 i 符合
2
中出現;
也就是說當 i 符合
2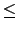 i
i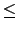 r 時
r 時
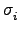 (a1) = a1 因此由
(a1) = a1 因此由
 =
= 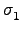 ...
... 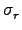 知
知
 (a1) = ( (a1) = (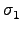 ... ... 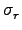 )(a1) = )(a1) = 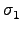 (a1) = a2. (a1) = a2. |
(3.5) |
不過由於
 =
= 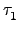 ...
... 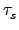 , a1 一定會在某一個
, a1 一定會在某一個 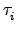 中出現, 否則如果 a1 在所有的
中出現, 否則如果 a1 在所有的 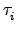 都沒出現則知
都沒出現則知
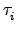 (a1) = a1, 然而若真如此, 則得
此和上式 (3.5)
相矛盾. 其實由於
(a1) = a1, 然而若真如此, 則得
此和上式 (3.5)
相矛盾. 其實由於
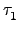 ,...,
,...,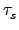 是 disjoint, a1
只會出現在唯一的
是 disjoint, a1
只會出現在唯一的 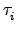 中. 我們不妨假設 a1 出現在
中. 我們不妨假設 a1 出現在
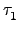 中 (別忘了
中 (別忘了
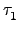 ,...,
,...,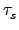 是 disjoint
所以它們可以兩兩交換). 因為 a1 不會在其他的
是 disjoint
所以它們可以兩兩交換). 因為 a1 不會在其他的 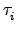 出現, 當 i
符合
2
出現, 當 i
符合
2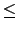 i
i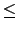 s 時, 我們有
s 時, 我們有
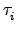 (a1) = a1. 因此知
(a1) = a1. 因此知
 (a1) = ( (a1) = (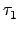 ... ... 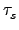 )(a1) = )(a1) = 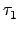 (a1). (a1). |
(3.6) |
結合 (3.5) 和 (3.6) 兩式, 我們得
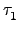 (a1) = a2.
也就是說
(a1) = a2.
也就是說
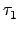
= (
a1 a2 ...
對 a2 用同樣的論述可得
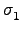 (a2) =
(a2) = 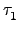 (a2), 如此一直下去我們可得
(a2), 如此一直下去我們可得
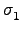 =
= 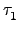 .
因此用歸納法可知 r = s 且 對所有的 i 皆有
.
因此用歸納法可知 r = s 且 對所有的 i 皆有
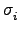 =
= 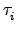 .
我們證得了 Sn 中所有的元素皆存在唯一的 disjoint cycle
decomposition.
.
我們證得了 Sn 中所有的元素皆存在唯一的 disjoint cycle
decomposition.


下一頁: Disjoint cycle 的性質
上一頁: The Symmetric Group
前一頁: The symmetric group of
Administrator
2005-06-18
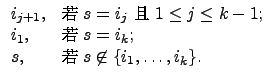
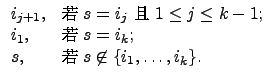
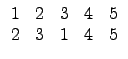
![]() 用 cycle 表示出來. 因
用 cycle 表示出來. 因
![]() 將
1
將
1 ![]() 2 所以我們先寫下
2 所以我們先寫下
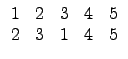
![]() {j1,..., jl} =
{j1,..., jl} = ![]() 則稱此兩
cycle 為 disjoint cycles. 如果將 Sn 中的元素寫成一些兩兩
disjoint 的 cycles 的乘積 (當然包括只有一個 cycle 的情況),
我們就稱之為 disjoint cycle decomposition. 如前面
(4 5)(1 2 3) 和
(1 3 5 2 4) 就分別是
則稱此兩
cycle 為 disjoint cycles. 如果將 Sn 中的元素寫成一些兩兩
disjoint 的 cycles 的乘積 (當然包括只有一個 cycle 的情況),
我們就稱之為 disjoint cycle decomposition. 如前面
(4 5)(1 2 3) 和
(1 3 5 2 4) 就分別是
![]() 和
和 ![]() 的 disjoint cycle decomposition.
的 disjoint cycle decomposition.
![]()
![]() Sn, 其 disjoint cycle
decomposition 是存在的. 作法就如同前面的例子, 任取一數
a1
Sn, 其 disjoint cycle
decomposition 是存在的. 作法就如同前面的例子, 任取一數
a1 ![]() {1,..., n} 我們先考慮
{1,..., n} 我們先考慮 ![]() 將 a1 送到何處? 若
將 a1 送到何處? 若
![]() (a1) = a1, 則知 a1 不會出現在 cycle decomposition 之中,
所以我們繼續考慮其他的數. 如果
(a1) = a1, 則知 a1 不會出現在 cycle decomposition 之中,
所以我們繼續考慮其他的數. 如果
![]() (a1) = a2
(a1) = a2![]() a1 則寫下
a1 則寫下
![]() 2,
2
2,
2 ![]() 3,
3
3,
3 ![]() 1. 因此我們將之視為同一
cycle (不過要注意
(1 3 2) 是不同的 cycle). 另外
(1 2 3)(4 5) 和
(4 5)(1 2 3)
也是同一個函數所以我們也將之視為同樣的 decomposition.
1. 因此我們將之視為同一
cycle (不過要注意
(1 3 2) 是不同的 cycle). 另外
(1 2 3)(4 5) 和
(4 5)(1 2 3)
也是同一個函數所以我們也將之視為同樣的 decomposition.
![]() {1,..., n} 但
x
{1,..., n} 但
x ![]() {a1,..., ak}, 則知
{a1,..., ak}, 則知
![]() (x) = x, 但由假設知
(x) = x, 但由假設知
![]() {a1,..., ak}, 假設 x = ai,
1
{a1,..., ak}, 假設 x = ai,
1![]() i
i![]() k - 2, 則
k - 2, 則
![]() 和
和 ![]() 是 disjoint, 所以
x
是 disjoint, 所以
x ![]() {1,..., n} 可分成三種情況: (a)
x
{1,..., n} 可分成三種情況: (a)
x ![]() {a1,..., ak}
{a1,..., ak} ![]() {b1,..., bl}; (b)
x
{b1,..., bl}; (b)
x ![]() {a1,..., ak}; (c)
x
{a1,..., ak}; (c)
x ![]() {b1,..., bl}.
{b1,..., bl}.
![]() (x) =
(x) = ![]() (x) = x 故
(x) = x 故
![]() (x)
(x) ![]() {a1,..., ak} 但由
disjoint 知 x 和
{a1,..., ak} 但由
disjoint 知 x 和 ![]() (x) 皆不屬於
{b1,..., bl} 故
(x) 皆不屬於
{b1,..., bl} 故
![]() (x) = x 且
(x) = x 且
![]() (
(![]() (x)) =
(x)) = ![]() (x). 所以知
(x). 所以知
![[*]](crossref.gif) 中我們證得
中我們證得
![[*]](crossref.gif) 可得
可得
![]() 和
和 ![]() 不是 disjoint 時, 則
不是 disjoint 時, 則
![]() .
. ![]() 並不一定等於
並不一定等於
![]() .
. ![]() (前面已給過例子了).
(前面已給過例子了).![]()
![]() Sn 有兩種 disjoint cycle decompositions:
Sn 有兩種 disjoint cycle decompositions:
![]() =
= ![]() ...
... ![]() 和
和
![]() =
= ![]() ...
... ![]() , 其中
, 其中
![]() ,...,
,...,![]() 和
和
![]() ,...,
,...,![]() 分別是兩組
disjoint cycles. 假設
a1
分別是兩組
disjoint cycles. 假設
a1 ![]() {1,..., n} 在
{1,..., n} 在 ![]() 這個 cycle
出現, 而
這個 cycle
出現, 而
![]() (a1) = a2, 則我們有
(a1) = a2, 則我們有