- (Act1)
-
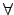 a
a  G, s
G, s  S, 皆有 a*s
S, 皆有 a*s  S.
S.
- (Act2)
-
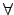 s
s  S, 皆有 e*s = s, 其中 e 是 G 的
identity.
S, 皆有 e*s = s, 其中 e 是 G 的
identity.
- (Act3)
-
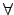 a, b
a, b  G, s
G, s  S, 皆有
(a . b)*s = a*(b*c).
S, 皆有
(a . b)*s = a*(b*c).
條件 (Act1) 是說 action 必須是封閉的, 也就是說 G 中的元素對 S
中的元素作用後還是要在 S 中. 這樣 G 中的元素就可以一直作用下去.
也就是說若 b ![]() G, s
G, s ![]() S, 則 b*s 會在 S 中所以 G 中的元素
a 才可以再對 b*s 作用得 a*(b*s). 就因如此 (Act3) 中 a*(b*s)
才有意義. (Act3) 告訴我們: b 對 s 作用後 a 再作用上去和
a . b 直接作用在 s 上是一樣的. 這有點像結合率對吧!
事實上若考慮 S = G, 而 G 對 G 的作用是 G 上的乘法,
則沒錯 G 上的乘法事實上就是一個 group action. 其實在證明 Theorem
3.4.15 時我們就引進了 Sn 對 n×n 矩陣的 group action.
我們不在這裡介紹其他的 group action 的例子,
我們留待要用到時再個別介紹.
S, 則 b*s 會在 S 中所以 G 中的元素
a 才可以再對 b*s 作用得 a*(b*s). 就因如此 (Act3) 中 a*(b*s)
才有意義. (Act3) 告訴我們: b 對 s 作用後 a 再作用上去和
a . b 直接作用在 s 上是一樣的. 這有點像結合率對吧!
事實上若考慮 S = G, 而 G 對 G 的作用是 G 上的乘法,
則沒錯 G 上的乘法事實上就是一個 group action. 其實在證明 Theorem
3.4.15 時我們就引進了 Sn 對 n×n 矩陣的 group action.
我們不在這裡介紹其他的 group action 的例子,
我們留待要用到時再個別介紹.
談 group action 最主要的原因就是想用 G 的 action 將 S
中的元素分類. 若 (G, S,*) 是一個 group action. 我們說
x, y ![]() S 是同類的 (記作 x
S 是同類的 (記作 x ![]() y) 若且為若存在 a
y) 若且為若存在 a ![]() G 使得
a*x = y. 我們曾說過一個好的分類必須是一個 equivalence relation.
下一個 Lemma 告訴我們當 (G, S,*) 是一個 group action 時,
這樣的分類是一個好的分類.
G 使得
a*x = y. 我們曾說過一個好的分類必須是一個 equivalence relation.
下一個 Lemma 告訴我們當 (G, S,*) 是一個 group action 時,
這樣的分類是一個好的分類.
(equiv1) 任取 x ![]() S, 由 (Act2) 知 e*x = x 故 x
S, 由 (Act2) 知 e*x = x 故 x ![]() x.
x.
(equiv2) 若 x ![]() y, 則由定義知: 存在 a
y, 則由定義知: 存在 a ![]() G 使得 a*x = y.
等式兩邊用 a-1 作用, 由 (Act2) 和 (Act3) 得
G 使得 a*x = y.
等式兩邊用 a-1 作用, 由 (Act2) 和 (Act3) 得
(equiv3) 若 x ![]() y 且 y
y 且 y ![]() z, 知存在 a, b
z, 知存在 a, b ![]() G 使得 a*x = y
且 b*y = z. 故由 (Act3) 知
(b . a)*x = b*(a*x) = b*y = z. 因為
b . a
G 使得 a*x = y
且 b*y = z. 故由 (Act3) 知
(b . a)*x = b*(a*x) = b*y = z. 因為
b . a ![]() G, 故知 x
G, 故知 x ![]() z.
z.
![]()
在第二章我們提過用 equivalence relation 分類的好處是 S 內的每一個元素都會被分到某一類, 且不同類的集合不會有交集. 現在若 S 是一個有限集合, 且 S 可分成 [x1],...,[xr] 這 r 個同類集, 其中 [xi] 表示 S 中與 xi 同類的元素所成的集合. 則由 Lemma 2.1.2 知
(2) 首先我們觀察若 y ![]() [x], 表示存在 a
[x], 表示存在 a ![]() G 使得 y = a*x. 反之,
若給定 a
G 使得 y = a*x. 反之,
若給定 a ![]() G, 令 y = a*x, 則 y 和 x 是同類. 所以我們知
[x] = {g*x | g
G, 令 y = a*x, 則 y 和 x 是同類. 所以我們知
[x] = {g*x | g ![]() G}, 也就是每個 [x] 中的元素都是 g*x
這種形式. 不過要注意有可能存在 a, b
G}, 也就是每個 [x] 中的元素都是 g*x
這種形式. 不過要注意有可能存在 a, b ![]() G 且 a
G 且 a![]() b 但 a*x = b*x.
所以要真正算出 [x] 有多少元素, 等於要算出到底有多少 G
中的元素會讓 g*x 相異. 然而若 a, b
b 但 a*x = b*x.
所以要真正算出 [x] 有多少元素, 等於要算出到底有多少 G
中的元素會讓 g*x 相異. 然而若 a, b ![]() G 且 a*x = b*x,
則在等式兩邊用 a-1 作用, 得
G 且 a*x = b*x,
則在等式兩邊用 a-1 作用, 得
Lemma 4.1.3 告訴我們, 給定 x ![]() S, 可由 Gx 得到 [x]
的訊息. 例如若 Gx = G (即所有 G 中的元素對 x 作用仍是 x),
則知 |[x]| = 1. 也就是說在 S 中和 x 同類的只有 x 本身,
其他的元素都和 x 不同類. 這樣的 x 對我們很有用, 我們將這種特別的
x 所成的集合記為 S0.
S, 可由 Gx 得到 [x]
的訊息. 例如若 Gx = G (即所有 G 中的元素對 x 作用仍是 x),
則知 |[x]| = 1. 也就是說在 S 中和 x 同類的只有 x 本身,
其他的元素都和 x 不同類. 這樣的 x 對我們很有用, 我們將這種特別的
x 所成的集合記為 S0.
回顧一下 G 是一個 p-group, 表示 | G| = pn 這種形式. 由 Lagrange
定理 (Theorem 2.2.2) 知 G 的所有的 subgroup 也是 p-group.
現若
x ![]() S0, 由定義知 Gx
S0, 由定義知 Gx![]() G, 因此 | Gx| = pm 其中
0
G, 因此 | Gx| = pm 其中
0![]() m < n. 也就是說 p 整除 | G|/| Gx|. 因此當
i
m < n. 也就是說 p 整除 | G|/| Gx|. 因此當
i ![]() {t + 1,..., r} 時, 由於
xi
{t + 1,..., r} 時, 由於
xi ![]() S0, 故由 Lemma
4.1.3 知 p 整除
|[xi]| = | G|/| Gxi|.
S0, 故由 Lemma
4.1.3 知 p 整除
|[xi]| = | G|/| Gxi|.
由於
最後我們要強調, 之後我們就是要利用 Proposition 4.1.4 來證明幾個重要的定理, 因此給了一個 group action, 要知道 S0 是哪些元素就顯得特別重要.