


下一頁: Sylow p-subgroup 的存在性
上一頁: First Sylow's Theorem
前一頁: First Sylow's Theorem
若 H 是 G 的一個 subgroup, 用
a-1 . b  H 表示 a, b
同類的分類方法, 我們在 Lemma 2.2.1 中知道和 a
同類的元素所成的集合可用
H 表示 a, b
同類的分類方法, 我們在 Lemma 2.2.1 中知道和 a
同類的元素所成的集合可用
a . H = {
a . h |
h  H
H}
來表示. 因此我們將用 a . H 來表示和 a 同類的元素所成的集合,
一般來說稱 a . H 這樣的集合為 H 在 G 中 的一個 left
coset. 我們再次強調一次若
a . H = b . H 表示
a-1 . b  H. 反之, 若
a . H
H. 反之, 若
a . H b . H, 則
a-1 . b
b . H, 則
a-1 . b 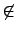 H.
H.
若 G 是一個 finite group, 且 H 是 G 的一個 subgroup. 令 S
為所有 H 在 G 中的 left coset 所成的集合. 換言之,
S = {
a . H |
a  G
G}.
也就是說我們將 a . H
看成是一個元素. 現在我們要定一個 H 對 S 的作用: 對任意的 h  H,
a . H
H,
a . H  S, 我們定義
S, 我們定義
h*(a . H) = (h . a) . H.
我們要證明這樣定的 (H, S,*) 是一個 group action. 首先證明 (Act1).
對任意的 h  H,
a . H
H,
a . H  S, 由於
h*(a . H) = (h . a) . H, 而 h . a 是 G 的一個元素, 由定義知它當然是 H 在
G 中的一個 left coset. 再來因
S, 由於
h*(a . H) = (h . a) . H, 而 h . a 是 G 的一個元素, 由定義知它當然是 H 在
G 中的一個 left coset. 再來因
e*(a . H) = (e . a) . H = a . H,
故知 (Act2) 也成立. 最後若 h, h'  H, 則對於任意的
a . H
H, 則對於任意的
a . H  S, 我們皆有
S, 我們皆有
h*(h'*(a . H)) = h*((h' . a) . H) = (h . (h' . a)) . H,
和
(h . h')*(a . H) = ((h . h') . a) . H.
所以利用結合率知 (Act3) 也成立.
S 是所有 H 在 G 中的 left coset 所成的集合, 也就是說 S
的個數就是 H 在 G 中分類後可分的類別個數. 我們在證明 Lagrange
定理 (Theorem 2.2.2) 時已算出此數為 | G|/| H|, 故得
| S| = 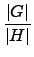 . . |
(4.9) |
什麼會是 S0 呢? 若
a . H  S0, 則對於所有 h
S0, 則對於所有 h  H 皆有
h*(a . H) = a . H. 然而
h*(a . H) = (h . a) . H,
這告訴我們
H 皆有
h*(a . H) = a . H. 然而
h*(a . H) = (h . a) . H,
這告訴我們
a . H = (h . a) . H.
也就是
a-1 . h . a  H. 所以若
a . H
H. 所以若
a . H  S0 則對於所有的 h
S0 則對於所有的 h  H, 皆有
a-1 . h . a
H, 皆有
a-1 . h . a  H. 反之, 若 a 符合對於所有的 h
H. 反之, 若 a 符合對於所有的 h  H,
皆有
a-1 . h . a
H,
皆有
a-1 . h . a  H, 則
a . H
H, 則
a . H  S0. 所以我們得到
S0. 所以我們得到
S0 = {a . H | a-1 . h . a  H, H, 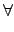 h h  H}. H}. |
(4.10) |
由於我們想了解 S0, 我們必須更深入的討論像 a 這種對於所有的
h  H, 皆有
a-1 . h . a
H, 皆有
a-1 . h . a  H 這樣性質的元素. 若 a
有這種性質, 由定義知
a-1 . H . a
H 這樣性質的元素. 若 a
有這種性質, 由定義知
a-1 . H . a  H. 由於 G
是一個 finite group, 由 Lemma 1.5.2 我們知
| a-1 . H . a| = | H|, 因此得
a-1 . H . a = H. 所以我們可以將式子
(4.10) 改寫成
H. 由於 G
是一個 finite group, 由 Lemma 1.5.2 我們知
| a-1 . H . a| = | H|, 因此得
a-1 . H . a = H. 所以我們可以將式子
(4.10) 改寫成
| S0 = {a . H | a-1 . H . a = H}. |
(4.11) |
其實我們常把符合
a-1 . H . a = H 的 a 所成的集合寫成
N(H), 也就是
N(
H) = {
a  G
G |
a-1 . H . a =
H}.
其實
N(H) 是 G 的一個 subgroup. 這是因為若
a, b  N(H), 則
a-1 . H . a = H 且
b-1 . H . b = H, 所以
N(H), 則
a-1 . H . a = H 且
b-1 . H . b = H, 所以
(b . a)-1 . H . (b . a) = a-1 . (b-1 . H . b) . a = a-1 . H . a = H.
也就是
b . a  N(H), 這證得了封閉性. 至於 inverse, 由於
a-1 . H . a = H, 所以
N(H), 這證得了封閉性. 至於 inverse, 由於
a-1 . H . a = H, 所以
a . (a-1 . H . a) . a-1 = a . H . a-1.
不過以上等式左邊等於 H,
而右邊可寫成
(a-1)-1 . H . a-1, 故知
a-1  N(H).
N(H).
若 h  H, 因 H 是一個 group, 我們知
h-1
H, 因 H 是一個 group, 我們知
h-1  H,
所以對於所有的 h'
H,
所以對於所有的 h'  H 皆有
h-1 . h' . h
H 皆有
h-1 . h' . h  H. 由此知
h-1 . H . h = H, 也就是 h
H. 由此知
h-1 . H . h = H, 也就是 h  N(H). 所以
H
N(H). 所以
H  N(H), 換句話說 H 是 N(H) 的一個 subgroup. 既然 H 是 N(H)
的一個 subgroup, 由 Lagrange 定理知 | H| 整除 | N(H)|.
別忘了由式子 (4.11) 我們有
S0 = {a . H | a
N(H), 換句話說 H 是 N(H) 的一個 subgroup. 既然 H 是 N(H)
的一個 subgroup, 由 Lagrange 定理知 | H| 整除 | N(H)|.
別忘了由式子 (4.11) 我們有
S0 = {a . H | a  N(H)}, 也就是說 S0 的個數應該是 N(H) 裡的元素用 H
分類後所得的類別個數, 因此我們有
N(H)}, 也就是說 S0 的個數應該是 N(H) 裡的元素用 H
分類後所得的類別個數, 因此我們有
| S0| = 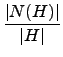 . . |
(4.12) |
我們要強調因 H 是 N(H) 的 subgroup,
所以在分類時至少有
e . H = H 這一類. 所以知
| S0|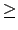 1. 1. |
(4.13) |
通常我們稱 N(H) 是 H 的 normalizer, 這是因為 H 不只是
N(H) 的 subgroup, 其實是 N(H) 的 normal subgroup. 要證 normal,
我們需要證: 給定 h  H, 對任意的 a
H, 對任意的 a  N(H) 皆有
a-1 . h . a
N(H) 皆有
a-1 . h . a  H. 然而
a-1 . H . a = H, 當然得
a-1 . h . a
H. 然而
a-1 . H . a = H, 當然得
a-1 . h . a  H. 我們將此寫成以下的 Lemma.
H. 我們將此寫成以下的 Lemma.
Lemma 4.4.1
若
H 是
G 的 subgroup. 令
N(
H) = {
a  G
G |
a-1 . H . a =
H}, 則
H 是
N(
H) 的一個 normal subgroup.



下一頁: Sylow p-subgroup 的存在性
上一頁: First Sylow's Theorem
前一頁: First Sylow's Theorem
Administrator
2005-06-18
![]() H,
a . H
H,
a . H ![]() S, 由於
h*(a . H) = (h . a) . H, 而 h . a 是 G 的一個元素, 由定義知它當然是 H 在
G 中的一個 left coset. 再來因
S, 由於
h*(a . H) = (h . a) . H, 而 h . a 是 G 的一個元素, 由定義知它當然是 H 在
G 中的一個 left coset. 再來因
![]() S0, 則對於所有 h
S0, 則對於所有 h ![]() H 皆有
h*(a . H) = a . H. 然而
h*(a . H) = (h . a) . H,
這告訴我們
H 皆有
h*(a . H) = a . H. 然而
h*(a . H) = (h . a) . H,
這告訴我們
![]() H, 皆有
a-1 . h . a
H, 皆有
a-1 . h . a ![]() H 這樣性質的元素. 若 a
有這種性質, 由定義知
a-1 . H . a
H 這樣性質的元素. 若 a
有這種性質, 由定義知
a-1 . H . a ![]() H. 由於 G
是一個 finite group, 由 Lemma 1.5.2 我們知
| a-1 . H . a| = | H|, 因此得
a-1 . H . a = H. 所以我們可以將式子
(4.10) 改寫成
H. 由於 G
是一個 finite group, 由 Lemma 1.5.2 我們知
| a-1 . H . a| = | H|, 因此得
a-1 . H . a = H. 所以我們可以將式子
(4.10) 改寫成
![]() H, 因 H 是一個 group, 我們知
h-1
H, 因 H 是一個 group, 我們知
h-1 ![]() H,
所以對於所有的 h'
H,
所以對於所有的 h' ![]() H 皆有
h-1 . h' . h
H 皆有
h-1 . h' . h ![]() H. 由此知
h-1 . H . h = H, 也就是 h
H. 由此知
h-1 . H . h = H, 也就是 h ![]() N(H). 所以
H
N(H). 所以
H ![]() N(H), 換句話說 H 是 N(H) 的一個 subgroup. 既然 H 是 N(H)
的一個 subgroup, 由 Lagrange 定理知 | H| 整除 | N(H)|.
別忘了由式子 (4.11) 我們有
S0 = {a . H | a
N(H), 換句話說 H 是 N(H) 的一個 subgroup. 既然 H 是 N(H)
的一個 subgroup, 由 Lagrange 定理知 | H| 整除 | N(H)|.
別忘了由式子 (4.11) 我們有
S0 = {a . H | a ![]() N(H)}, 也就是說 S0 的個數應該是 N(H) 裡的元素用 H
分類後所得的類別個數, 因此我們有
N(H)}, 也就是說 S0 的個數應該是 N(H) 裡的元素用 H
分類後所得的類別個數, 因此我們有 ![]() H, 對任意的 a
H, 對任意的 a ![]() N(H) 皆有
a-1 . h . a
N(H) 皆有
a-1 . h . a ![]() H. 然而
a-1 . H . a = H, 當然得
a-1 . h . a
H. 然而
a-1 . H . a = H, 當然得
a-1 . h . a ![]() H. 我們將此寫成以下的 Lemma.
H. 我們將此寫成以下的 Lemma.