Unique factorization domain 的基本性質

對於一般的 unique factorization domain R 由於 R 不一定是 Euclidean domain, 所以無法用類似輾轉相除法的方法求 greatest common divisor. 然而若 a, b $\in$ R, 我們可以利用 unique factorization domain 的性質將 a, b 分解成

証明. 利用 Lemma 8.1.6 我們只要證明 R 中任意兩個非 0 元素 a 和 b 的 greatest common divisor 存在即可.

首先我們將 a, b 的分解寫成式子 (8.1) 的形式, 且令

d = p₁^{t₁ ...}p_r^t_r,

其中 t_i = min{n_i, m_i}. 我們要證明 d 是 a, b 的 greatest common divisor.

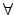首先由 t_i $\le$ m_i 以及 t_i $\le$ n_i, $\forall$ i = 1,..., r, 很容易得知 d | a 且 d | b. 因此知 d 是 a, b 的 common divisor. 痍Y c 是 a, b 的一個 common divisor, 假設 p 是一個 irreducible element 且 p | c, 則由 p | a 且 p | b 知 p 一定和 p₁,..., p_r 中某一個 p_i associates. 這告訴我們在 c 的分解中不可能出痔M p₁,..., p_r 不 associates 的 irreducible divisor, 也就是說我們也可將 c 分解成

c = w^.p₁^{s₁ ...}p_r^s_r,

其中 w 是 unit 且 s_i 是非負整數. 畢p果有個 i 符合 s_i > n_i, 為了方便就假設 s₁ > n₁ 吧! 利用 p₁^s₁ | c 以及 c | a 知 p₁^s₁ | a. 換言之

p₁^{s₁ - n₁} | p₂^{n₂ ...}p_r^n_r.

由 s₁ - n₁ $\ge$ 1 得

p₁ | p₂^{n₂ ...}p_r^n_r.

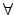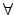然而 p₁ 是 prime, 這表示 p₁ 和 p₂,..., p_r 中某個 p_i associates. 這和當初假設 p₁,..., p_r 兩兩不 associates 相矛盾, 故得 s_i $\le$ n_i, $\forall$ i = 1,..., r. 同理 s_i $\le$ m_i, $\forall$ i = 1,..., r. 故得知對所有的 i = 1,..., r 皆有 s_i $\le$ min{n_i, m_i} = t_i. 也就是說 c | d. 故知 d 是 a, b 的 greatest common divisor. $\qedsymbol$

在前面幾節中要證明一個 integral domain 是一個 unique factorization domain, 我們都去證明這個 integral domain 中的 irreducible elements 和 prime elements 是一樣的. 事實上, 在 unique factorization domain 中 irreducible element 和 prime element 總是相同的.

証明. 我們已知在一個 integral domain 中 prime element 會是 irreducible element (Lemma 8.1.8). 所以我們只要證明 irreducible element 也會是 prime element.

假設 p $\in$ R 是一個 irreducible element 且 p | a^.b, 其中 a, b $\in$ R. 由假設知存在 h $\in$ R 滿足 a^.b = h^.p. 首先我們將 a, b 用式子 (8.1) 的形式分解, 因此有

a^.b = (u^.v)^.p₁^{n₁ + m₁ ...}p_r^{n_r + m_r}.

利用 R 是 unique factorization domain, 由 a^.b 的分解知 p 一定和 p₁,..., p_r 中某一個 p_i associates. 然而 n_i 和 m_i 不同時為 0, 也就是說 n_i $\ne$ 0 或 m_i $\ne$ 0. 若 n_i $\ne$ 0, 則知 p | a, 而若 m_i $\ne$ 0 則有 p | b. 故得證 p 是 prime element. $\qedsymbol$