next up previous
下一頁: FIELD 上一頁: Unique Factorization Domain 前一頁: Unique factorization domain 的基本性質

Polynomials over unique factorization domain

我們將利用類似推導 $ \mathbb {Z}$[x] 是 unique factorization domain 的方法推導當 R 是 unique factorization domain 時

R[x] = {anxn + ... + a1x + a0 | ai $\displaystyle \in$ R}

這種以 R 為係數的 polynomials 所形成的 polynomial ring 是一個 unique factorization domain.

若 f (x) $ \in$ R[x] 且 f (x)$ \ne$ 0, 則我們可將 f (x) 寫成 f (x) = anxn + ... + a1x + a0, 其中 an$ \ne$ 0. 如同前面討論 F[x] 的情況我們可以定義 deg(f (x)) = n. 利用和 Lemma 7.2.2 同樣的證明我們可以得到: 若 f (x), g(x) $ \in$ R[x] 且皆不為 0, 則

deg(f (x) . g(x)) = deg(f (x)) + deg(g(x)).

主要的原因是 Lemma 7.2.2 的証明僅用到兩個非 0 元素相乘不為 0 (即 integral domain) 的性質, 並沒有用到 field 的性質. 利用 degree 的這個特性我們馬上有以下的性質.

Lemma 8.4.3   令 R 是一個 integral domain.
  1. R[x] 也是一個 integral domain.
  2. R[x] 中的 unit 就是 R 中的 unit.
  3. 若 a $ \in$ R 是 R 中的 irreducible element 則 a 看成是 R[x] 中的元素 (即常數多項式) 時也是 irreducible.

証 明. (1) 若 f (x)$ \ne$ 0 且 g(x)$ \ne$ 0, 假設 f (x) 的最高次項係數是 an 且 g(x) 的最高次項係數是 bm, 則 f (x) . g(x) 的最高次項係數是 an . bm. 由於 an, bm $ \in$ R, 且 an$ \ne$, bm$ \ne$ 0 利用 R 是 integral domain 知 an . bm$ \ne$ 0. 也就是說 f (x) . g(x) 不可能為 0 多項式.

(2) 若 f (x) $ \in$ R[x] 是 R[x] 中的 unit, 則利用存在 g(x) $ \in$ R[x] 滿足 f (x) . g(x) = 1 知 deg(f (x)) + deg(g(x)) = 0 (注意 1 是常數多項式故 degree 為 0). 故得 deg(f (x)) = deg(g(x)) = 0. 換句話說 f (x), g(x) 都是常數多項式, 也就是說 f (x), g(x) $ \in$ R. 然而由假設 f (x) . g(x) = 1 知 f (x) 是 R 中的 unit.

(3) 假設 a $ \in$ R 是 R 中的 irreducible element. 注意由 degree 的性質知若 g(x) 是 f (x) 的 divisor (由於存在 h(x) $ \in$ R[x] 滿足 g(x) . h(x) = f (x)), 則 deg(g(x))$ \le$deg(f (x)). 痍Y將 a 看成是常數多項式, 由於 deg(a) = 0, 故知在 R[x] 中 a 的 divisor 其 degree 也是 0. 換句話說在 R[x] 中 a 的 divisor 都是 R 的元素. 故利用 a 在 R 中是 irreducible 知這些 divisor 要不是 R 中的 unit 就是和 a associates. 然而由 (2) 知 R 中的 unit 當然也是 R[x] 中的 unit, 故知 a 在 R[x] 依然是 irreducible. $ \qedsymbol$

當 R 是一個 unique factorization domain 時, 令 F 為 R 的 quotient field. 接下來我們想利用 R 和 F[x] 都是 unique factorization domain (Theorem 7.2.14) 證明 R[x] 是一個 unique factorization domain.

為了將 R[x] 和 F[x] 的關係相連結, 我們還是得介紹和 $ \mathbb {Z}$[x] 中類似的 content 的概念. 首先由 Proposition 8.4.1 知若 f (x) = anxn + ... a1x + a0 $ \in$ R[x], 則 an,..., a1, a0 的 greatest common divisor 是存在的.

Definition 8.4.4   若 f (x) = anxn + ... + a1x + a0 $ \in$ R[x] 且 an,..., a1, a0 的 greatest common divisor 是 R 中的 unit, 則稱 f (x) 是 R[x] 中的 primitive polynomial.

Lemma 8.4.5   假設 R 是一個 unique factorization domain, 則對任意 f (x) $ \in$ R[x] 且 f (x)$ \ne$ 0, 都可找到 c $ \in$ R 且 f*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial 滿足

f (x) = c . f*(x).

又假設

f (x) = c . f*(x)  
  = c' . g(x)  

其中 c, c' $ \in$ R, 且 f*(x), g(x) $ \in$ R[x] 是 R[x] 的 primitive polynomials, 則 c $ \sim$ c' 且 f*(x) $ \sim$ g(x).

証 明. 首先證明存在性: 若 f (x) = anxn + ... + a1x + a0, 令 c 為 an,..., a1, a0 的 greatest common divisor. 所以對所有的 i = 0, 1,..., n 皆有 ai = c . bi, 其中 bi $ \in$ R, 而且 b0,..., bn 的 greatest common divisor 是 R 的 unit. 故令 f*(x) = bnxn + ... + b1x + b0, 則 f*(x) 是 R[x] 的 primitive polynomial 且 f (x) = c . f*(x). 故得證存在性.

接著證明唯一性: 若 f (x) = c' . g(x), 其中 g(x) 是 R[x] 的 primitive polynomial. 假設 g(x) = an'xn + ... + a1'x + a0', 則對所有 i = 0, 1,..., n, 皆有 ai = c' . ai'. 換句話說 c' 是 an,..., a0 的一個 common divisor. 因此由 c 是 an,..., a0 的 greatest common divisor 知 c' | c. 即存在 d $ \in$ R 使得 c = c' . d. 利用 ai = c . bi = c' . ai', 我們知對所有的 i = 0, 1,..., n, 皆有

c' . (d . bi) = (c' . d ) . bi = c . bi = c' . ai'.

例用 c'$ \ne$ 0 且 R 是 integral domain, 可得對所有的 i = 0, 1,..., n, 皆有 ai' = d . bi. 換句話說 d 是 an',..., a0' 的一個 common divisor. 然而由假設 an',..., a0' 的 greatest common divisor 是 unit, 故得 d 是 R 的一個 unit. 換句話說 c $ \sim$ c'. 再利用 f (x) = c . f*(x) = c' . g(x), 以及 R[x] 是 integral domain, 得 d . f*(x) = g(x). 由於 d 是 R 的 unit 也是 R[x] 的 unit, 故得 f*(x) $ \sim$ g(x). $ \qedsymbol$

利用 Lemma 8.4.5 的唯一性, 我們自然有以下的定義.

Definition 8.4.6   假設 R 是一個 unique factorization domain. 若 f (x) $ \in$ R[x] 可寫成 f (x) = c . f*(x) 其中 c $ \in$ R 且 f*(x) 是 R[x] 的 primitive polynomial, 則稱 c 為 f (x) 的 content, 定為 c(f ).

要注意由 Lemma 8.4.5 的證明我們知道 f (x) 的 content 其實就是 f (x) 所有係數的 greatest common divisor. 另� 要注意的是 f (x) 的 content 其實並不是一個固定的值, content 之間會差個 associates.

我們可以將 content 的定義推廣到 F[x]. 別忘了 F 是 R 的 quotient field, 所以 F 中每個元素都可以寫成 a/b 的形式, 其中 a, b $ \in$ R 且 b$ \ne$ 0. 硃鴷艩N的 f (x) = rnxn + ... + r1x + r0 $ \in$ F[x], 由於對任意的 i = 0, 1,..., n, 皆有 ri = ai/bi, 其中 ai, bi $ \in$ R, 我們可找到 d $ \in$ R 且 d$ \ne$ 0 使得 d . f (x) $ \in$ R[x] (比方說令 d = bn ... b0). 因此利用 Lemma 8.4.5 知存在 c $ \in$ R 以及 f*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial 使得 d . f (x) = c . f*(x). 由於 d$ \ne$ 0, 我們可將 f (x) 寫成

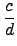f (x) = $\displaystyle {\frac{c}{d}}$ . f*(x).

換句話說任意 F[x] 中非 0 的 polynomial f (x) 皆可寫成 f (x) = r . f*(x), 其中 r $ \in$ F 且 f*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial. 我們依然稱此 r 是 f (x) 的 content 且仍記作 c(f ).

Corollary 8.4.7   假設 R 是一個 unique factorization domain, 且 F 是 R 的 quotient field. 則對任意 f (x) $ \in$ F[x] 且 f (x)$ \ne$ 0, 都可找到 c $ \in$ F 且 f*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial 滿足

f (x) = c . f*(x).

又假設

f (x) = c . f*(x)  
  = c' . g(x)  

其中 c, c' $ \in$ F, 且 f*(x), g(x) $ \in$ R[x] 是 R[x] 的 primitive polynomials, 則存在 u $ \in$ R 是 R 的 unit 使得 c = u . c' 且 u . f*(x) = g(x).

証 明. 前面已證存在性, 我們僅證唯一性. 我們將 c 和 c' 分別寫成 c = a/b 且 c' = a'/b', 其中 a, a', b, b' $ \in$ R 且 b$ \ne$ 0, b'$ \ne$ 0. 將 f (x) 乘上 b . b', 我們有 (b . b') . f (x) $ \in$ R[x] 且
(b . b') . f (x) = (a . b') . f*(x)  
  = (a' . b) . g(x).  

既然 (b . b') . f (x) $ \in$ R[x] 我們可以將 Lemma 8.4.5 套用在 (b . b') . f (x) 上, 故知存在 u $ \in$ R 是 R 中的 unit 滿足 a . b' = u . (a' . b). 也就是說 c = u . c'. 再利用 c'$ \ne$ 0 及 F[x] 是 integral domain 得 u . f*(x) = g(x). $ \qedsymbol$

和 $ \mathbb {Z}$[x] 一樣的狀況, 我們有以下的 Gauss Lemma 來幫助我們計算兩個 polynomials 相乘後之 content.

Lemma 8.4.8 (Gauss)   假設 R 是一個 unique factorization domain. 若 f (x), g(x) $ \in$ R[x] 是 R[x] 中的 primitive polynomials, 則 f (x) . g(x) 依然是 R[x] 中的 primitive polynomial.

証 明. 我們利用和 Lemma 7.3.5 相同的証明, 所以只給大略的証明. 假設 f (x) . g(x) 不是 primitive polynomial, 表示 f (x) . g(x) 所有係數的 greatest common divisor 不是 R 中的 unit. 因此利用 R 是 unique factorization domain 知存在 p $ \in$ R 是 R 中的一個 irreducible (也是 prime) element 是 f (x) . g(x) 所有係數的 common divisor. 然而 f (x) 和 g(x) 皆是 primitive polynomials, p 不可能整除所有 f (x) 的係數也不可能整除所有 g(x) 的係數. 所以若 i 是最小的數使得 f (x) 的 xi 項係數不能被 p 整除, 而 j 是最小的數使得 g(x) 的 xj 項係數不能被 p 整除, 則很容易看出 f (x) . g(x) 的 xi + j 項係數不可能被 p 整除. 這和 p 是 f (x) . g(x) 各項係數的 common divisor 矛盾, 故得證 f (x) . g(x) 是 R[x] 的 primitive polynomial. $ \qedsymbol$

Primitive polynomial 在 R[x] 中是和 F[x] 溝通的橋樑, 事實上在 R[x] 中不是常數的 irreducible element 都是 primitive polynomial.

Lemma 8.4.9   假設 R 是一個 unique factorization domain. 若 f (x) $ \in$ R[x] 是 R[x] 的 irreducible element 且 deg(f (x))$ \ge$1, 則 f (x) 是 R[x] 中的 primitive polynomial.

証 明. 若 f (x) 是 R[x] 中的 irreducible element, 由於 f (x) 可寫成 f (x) = c(f ) . f*(x) 其中 c(f ) $ \in$ R $ \subseteq$ R[x] 且 f*(x) $ \in$ R[x], 故知 c(f ) 是 f (x) 的一個 divisor. 由 f (x) 是 irreducible element 的假設知 c(f ) 是 R 中的 unit (f (x) 不可能和 c(f ) associates 因 deg(f (x))$ \ge$1 但 deg(c(f )) = 0), 故知 f (x) 是 primitive polynomial. $ \qedsymbol$

若 f (x), g(x) $ \in$ R[x], 由於 R $ \subseteq$ F, f (x) 和 g(x) 可同時看成是 R[x] 的 polynomials 也可以看成是 F[x] 的 polynomials. 因此這兩個 polynomials 間關係看成是 R[x] 或 F[x] 中的情況就會不同. 例如若 g(x) = f (x) . h(x), 其中 h(x) $ \in$ R[x] 我們就說 f (x) | g(x) in R[x]. 然而若 h(x) $ \in$ F[x], 我們就說 f (x) | g(x) in F[x]. 由於 R[x] $ \subseteq$ F[x], 很自然的我們知道若 f (x) | g(x) in R[x] 則 f (x) | g(x) in F[x]. 然而一般來說 f (x) | g(x) in F[x] 不見得會有 f (x) | g(x) in R[x]. 不過當 f (x) 是 R[x] 的 primitive polynomial 時, 就對了.

Lemma 8.4.10   假設 R 是一個 unique factorization domain 且 F 是 R 的 quotient field. 假設 f (x), g(x) $ \in$ R[x] 且 f (x) 是 R[x] 的一個 primitive polynomial, 則 f (x) | g(x) in F[x] 若且唯若 f (x) | g(x) in R[x].

証 明. 我們只要證明: 若 f (x) | g(x) in F[x] 則 f (x) | g(x) in R[x]. 由假設知存在 h(x) $ \in$ F[x] 使得 g(x) = f (x) . h(x). 利用 content, 我們得

c(g) . g*(x) = (c(f ) . c(h)) . (f*(x) . h*(x)).

其中 c(g), c(f ) $ \in$ R 是 g(x), f (x) 的 content, 而 c(h) $ \in$ F 是 h(x) 的 content, 且 g*(x), f*(x) 以及 h*(x) 都是 R[x] 的 primitive polynomials. 利用 Lemma 8.4.8 知 f*(x) . h*(x) 是 R[x] 的 primitive polynomial. 再利用 Corollary 8.4.7 知存在 u $ \in$ R 是 R 的 unit 滿足 u . c(g) = c(f ) . c(h). 然而由 f (x) 是 R[x] 的 primitive polynomial, 知 c(f ) 是 R 的 unit. 又由假設 g(x) $ \in$ R[x] 知 c(g) $ \in$ R. 故得

c(h) = c(f )-1 . u . c(g) $\displaystyle \in$ R.

然而 h(x) = c(h) . h*(x), 故由 c(h) $ \in$ R 以及 h*(x) $ \in$ R[x] 可得 h(x) $ \in$ R[x]. 換句話說 f (x) | g(x) in R[x]. $ \qedsymbol$

利用 Lemma 8.4.10 我們可以得到 R[x] 和 F[x] 中 prime element 的關係.

Corollary 8.4.11   假設 R 是一個 unique factorization domain 且 F 是 R 的 quotient field 且假設 p(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial. 若 p(x) 是 F[x] 中的 prime element 則 p(x) 是 R[x] 中的 prime element.

証 明. 假設 p(x) 是 F[x] 中的 prime element. 要證明 p(x) 是 R[x] 中的 prime element, 我們必須證明若 p(x) | f (x) . g(x) in R[x], 其中 f (x), g(x) $ \in$ R[x], 則 p(x) | f (x) in R[x] 或 p(x) | g(x) in R[x]. 因 p(x) 是 R[x] 中的 primitive polynomial, 由 Lemma 8.4.10 我們有 p(x) | f (x) . g(x) in F[x]. 故利用 p(x) 是 F[x] 的 prime element, 我們知 p(x) | f (x) in F[x] 或 p(x) | g(x) in F[x]. 再一次利用 Lemma 8.4.10, 我們知 p(x) | f (x) in R[x] 或 p(x) | g(x) in R[x], 故得證 p(x) 是 R[x] 的 prime element. $ \qedsymbol$

另� 在 R[x] 和 F[x] 中要區分清楚的是一個 R[x] 中的 polynomial 在 R[x] 和 F[x] 中可否分解 (即是否 irreducible) 的關聯性.

Lemma 8.4.12   假設 R 是一個 unique factorization domain 且 F 是 R 的 quotient field 且假設 f (x) $ \in$ R[x] 及 deg(f (x))$ \ge$1. 若存在 g(x), h(x) $ \in$ F[x] 滿足 deg(g(x))$ \ge$1 且 deg(h(x))$ \ge$1, 使得 f (x) = g(x) . h(x), 則存在 m(x), n(x) $ \in$ R[x] 滿足 deg(g(x)) = deg(m(x)) 且 deg(h(x)) = deg(n(x)) 使得 f (x) = m(x) . n(x).

証 明. 利用 content 我們將 f (x) = g(x) . h(x) 寫成:

c(f ) . f*(x) = (c(g) . c(h)) . (g*(x) . h*(x)),

其中 c(f ) $ \in$ R, c(g), c(h) $ \in$ F, 而 f*(x), g*(x) 和 h*(x) 都是 R[x] 的 primitive polynomial. 利用 Lemma 8.4.8 知 g*(x) . h*(x) 是 R[x] 的 primitive polynomial, 故由 Lemma 8.4.5 知存在 u $ \in$ R 是 R 的 unit 使得 c(g) . c(h) = c(f ) . u. 換言之, c(g) . c(h) $ \in$ R. 故若令 m(x) = (c(g) . c(h)) . g*(x) $ \in$ R[x], n(x) = h*(x), 則 m(x), n(x) 符合定理所要求. $ \qedsymbol$

由 Lemma 8.4.12 我們可得 R[x] 和 F[x] 間 irreducible element 的關係.

Corollary 8.4.13   假設 R 是一個 unique factorization domain 且 F 是 R 的 quotient field. 若 p(x) $ \in$ R[x] 滿足 deg(p(x))$ \ge$1 是 R[x] 的 primitive polynomial, 則 p(x) 是 R[x] 的 irreducible element 若且唯若 p(x) 是 F[x] 的 irreducible element.

証 明. 首先假設 p(x) 是 R[x] 的 irreducible element, 要證明 p(x) 也是 F[x] 的 irreducible element. 假如 p(x) 在 F[x] 不是 irreducible element, 則存在 g(x), h(x) $ \in$ F[x] 滿足 deg(g(x))$ \ge$1 且 deg(h(x))$ \ge$1 使得 p(x) = g(x) . h(x). 故由 Lemma 8.4.12 知存在 m(x), n(x) $ \in$ R[x] 滿足 deg(m(x))$ \ge$1 且 deg(n(x))$ \ge$1 使得 p(x) = m(x) . n(x). 換句話說由 1$ \le$deg(m(x)) < deg(p(x)) 知, m(x) 是 p(x) 在 R[x] 的一個 divisor 且既不是 unit 也不和 p(x) associates. 故知 p(x) 不是 R[x] 的 irreducible element. 此和假設矛盾, 故知 p(x) 是 F[x] 的 irreducible element.

反之, 假設 p(x) 是 F(x) 的 irreducible element. 如果 p(x) 在 R[x] 中不是 irreducible, 即存在 l (x), m(x) $ \in$ R[x] 滿足 p(x) = l (x) . m(x), 其中 l (x) 和 m(x) 都不是 R[x] 中的 unit. 但 l (x), m(x) $ \in$ R[x] $ \subseteq$ F[x], 故利用 p(x) 是 F[x] 中的 irreducible element 知 l (x) 和 m(x) 中必有一個是 F[x] 中的 unit (即常數多項式). 就假設是 l (x) = a $ \in$ R 吧! 由假設 a 不能是 R 的 unit, 否則 l (x) = a 是 R[x] 的 unit (Lemma 8.4.3). 然而由 f (x) = l (x) . m(x) = a . m(x) 且 m(x) $ \in$ R[x] 知 a 是 f (x) 各項係數之 common divisor, 即 a | c(f ) in R. 但由假設 f (x) 是 primitive polynomial 知 c(f ) 是 R 中的 unit, 故由 a | c(f ) in R 知 a 是 R 的 unit; 此和 a 不是 R 的 unit 相矛盾. 故知 f (x) 在 R[x] 中是 irreducible. $ \qedsymbol$

接著我們來看證明 R[x] 是 unique factorization domain 最關鍵的性質.

Proposition 8.4.14   假設 R 是一個 unique factorization domain, 則 R[x] 中的 irreducible element 和 prime element 是相同的.

証 明. 由於 R[x] 是 integral domain, 我們知 R[x] 的 prime element 就是 irreducible element (Lemma 8.1.8). 因此只要證明若 f (x) $ \in$ R[x] 是一個 irreducible element, 則 f (x) 是一個 prime element. 我們想藉由 F[x] (這裡 F 是 R 的 quotient field) 中的 irreducible element 是 prime element (Proposition 7.2.11) 來證明.

首先考� deg(f (x)) = 0 (即 f (x) = a $ \in$ R 是常數) 的情形. 因 a $ \in$ R 是 irreducible 且 R 是 unique factorization domain, 由 Proposition 8.4.2 知 a 是 R 的 prime element. 我們要證明 a 也是 R[x] 中的 prime element. 假設 g(x), h(x) $ \in$ R[x] 滿足 a | g(x) . h(x) in R[x], 即存在 l (x) $ \in$ R[x] 使得 a . l (x) = g(x) . h(x). 利用 content 得

(a . c(l )) . l*(x) = (c(g) . c(h)) . (g*(x) . h*(x)),

其中 c(l ), c(g), c(h) $ \in$ R 且 l*(x), g*(x), h*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomials. 由 Lemma 8.4.8 知 g*(x) . h*(x) 依然是 primitive polynomial, 故由 Lemma 8.4.5 知存在 u $ \in$ R 是 R 的 unit 滿足

u . a . c(l )= c(g) . c(h),

換句話說 a | c(g) . c(h) in R. 利用 a 是 R 的 prime element 之假設得 a | c(g) 或 a | c(h). 然而 g(x) = c(g) . g*(x), 故若 a | c(g) 則 a | g(x). 同理若 a | c(h), 則 a | h(x). 故知 a = f (x) 是 R[x] 中的 prime element.

畢瓞 deg(f (x))$ \ge$1 的情形. 令 F 是 R 的 quotient field. 因為 f (x) 是 R[x] 的 irreducible element 由 Corollary 8.4.13 知 f (x) 是 F[x] 的 irreducible element. 然而 Proposition 7.2.11 告訴我們此時 f (x) 也是 F[x] 中的 prime element. 由於 Lemma 8.4.9 告訴我們 f (x) 是 R[x] 的 primitive polynomial, 故可套用 Corollary 8.4.11 得證 f (x) 也是 R[x] 中的 prime element. $ \qedsymbol$

畢b我們有足夠的性質來幫助我們證明 R[x] 也是一個 unique factorization domain. 大家可以沿用證明 $ \mathbb {Z}$[x] 是 unique factorization domain (Theorem 7.3.13) 的方法來處理. 這裡我們想藉由 F[x] 是 unique factorization domain (Theorem 7.2.14) 這個事實來推導. 這個證明不見的比較簡明, 不過可以幫助我們多了解 R[x] 和 F[x] 間的關聯.

Theorem 8.4.15   假設 R 是一個 unique factorization domain, 則 R[x] 也是一個 unique factorization domain.

証 明. 令 F 是 R 的 quotient field.

首先證明存在性: 即任一 R[x] 中非 0 且不是 unit 的元素 f (x) 可寫成有限多個 R[x] 的 irreducible elements 的乘積. 首先將 f (x) 寫成 f (x) = c(f ) . f*(x), 其中 c(f ) $ \in$ R 且 f*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial. 若 c(f ) 不是 unit, 則利用 R 是 unique factorization domain 我們可以將 c(f ) 寫成有限多個 R 中的 irreducible elements 的乘積. 利用 Lemma 8.4.3 (3) 知道 c(f ) 可以寫成有限多個 R[x] 中的 irreducible elements 的乘積. 所以我們只要證明 f*(x) 可以寫成有限多個 irreducible elements 的乘積. 盛N f*(x) 看成是 F[x] 中的元素, 則利用 F[x] 是 unique factorization domain, 知道 f*(x) = p1(x) ... pm(x), 其中 p1(x),..., pm(x) $ \in$ F[x] 是 F[x] 中的 irreducible elements. 再利用 content, 知每個 pi(x) 都可寫成 pi(x) = c(pi) . pi*(x), 其中 pi*(x) $ \in$ R[x] 是 R[x] 的 primitive polynomial. 換句話說

f*(x) = (c(p1) ... c(pm)) . p1*(x) ... pm*(x).

利用 Lemma 8.4.8 知 p1*(x) ... pm*(x) 是 R[x] 的 primitive polynomial, 故由 f*(x) 是 R[x] 的 primitive polynomial 以及 Lemma 8.4.5 知 c(p1) ... c(pm) = u 是 R 中的 unit, 由 Lemma 8.4.3 知 u 也是 R[x] 的 unit. 因此我們只要證明 p1*(x),...pm*(x) 是 R[x] 中的 irreducible elements 就可. 如此一來

f*(x) = (u . p1*(x)) . p2*(x) ... pm*(x),

所以 f*(x) 可以寫成有限多個 irreducible elements 的乘積 (注意 u . p1*(x) 和 p1*(x) associates, 所以也是 R[x] 中的 irreducible element). 然而因 pi(x) = c(pi) . pi*(x), 由 pi(x) 在 F[x] 中 irreducible 知 pi*(x) 也是 F[x] 的 irreducible element. 由於 pi*(x) 是 R[x] 的 primitive polynomial, 套用 Corollary 8.4.13 知 pi*(x) 也是 R[x] 的 irreducible element.

接著證明分解的唯一性: 其實我們可以利用 Proposition 8.4.14 直接證明唯一性, 不過這裡我們依然利用 F[x] 和 R 是 unique factorization domain 來證明. 首先假設

f (x) = (a1n1 ... arnr) . p1nr + 1(x) ... pvnr + v(x)  
  = (b1m1 ... bsms) . q1ms + 1(x) ... qwms + w(x),  

其中 a1,...ar $ \in$ R (即 deg(ai) = 0) 是 R[x] 中兩兩不 associates 的 irreducible elements 而 p1(x),..., pv(x) $ \in$ R[x] 是 R[x] 中兩兩不 associates 且 degree 大於 0 的 irreducible elements, 對於 b1,..., bs $ \in$ R 以及 q1(x),..., qw(x) $ \in$ R[x] 也是同樣的假設. 首先注意由於這些 pi(x) 和 qj(x) 都是 R[x] 中的 irreducible elements 且 deg(pi(x))$ \ge$1 以及 deg(qj(x))$ \ge$1, 由 Lemma 8.4.9 知這些 pi(x) 和 qj(x) 都是 primitive polynomial, 故由 Lemma 8.4.8 以及 Lemma 8.4.5 知存在 R 中的 unit u 滿足

a1n1 ... arnr = u . b1m1 ... bsms,

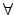故利用 R 是 unique factorization domain 的性質知經過適當順序掉換我們有 r = s, ai $ \sim$ bi 且 ni = mi, $ \forall$ i = 1,..., r. 所以最後我們只要考�
f0(x) = u . p1nr + 1(x) ... pvnr + v(x)  
  = q1ms + 1(x) ... qwms + w(x)  

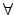這一部分的唯一性. 由於 f0(x) $ \in$ R[x] $ \subseteq$ F[x], 且 pi(x), qi(x) 是 R[x] 中的 irreducible elements 所以也是 F[x] 中的 irreducible elements (Corollary 8.4.13), 故利用 F[x] 是 unique factorization domain 知經過重排後 v = w, pi(x) = ki . qi(x) 且 ni = mi, $ \forall$ i = r + 1,...r + v, 其中 ki $ \in$ F. 然而 pi(x) 和 qi(x) 都是 R[x] 的 primitive polynomial, 故知 ki 是 R 的 unit. 換言之, 對所有的 i = r + 1,..., r + v, 皆有 pi(x) $ \sim$ qi(x). 故得證唯一性. $ \qedsymbol$

最後我們來看 Theorem 8.4.15 一個重要的應用. 若 R 是一個 unique factorization domain, 由 Theorem 8.4.15 知 R' = R[x] 也是一個 unique factorization domain. 畢瓞 R'[y] 這一個以 y 為變數 R' 的元素為係數的 polynomial ring, 也就是 R'[y] 的元素都是

fn(x)yn + fn - 1(x)yn - 1 + ... + f1(x)y + f0(x),

其中對所有的 i = 0, 1,..., n, fi(x) $ \in$ R' = R[x] 是係數在 R 的 x 的多項式. 很容易看出 R'[y] = R[x][y] = R[x, y] 就是以 R 的元素為係數 x, y 為變數的兩個變數的多項式所成的集合, 故再次由 Theorem 8.4.15 知 R[x, y] 是 unique factorization domain. 我們可以將以上的論述推廣到 R[x1,..., xn] 這個以 R 的元素為係數 x1,..., xn 為變數的 n 個變數的 polynomial ring:

Theorem 8.4.16   假設 R 是一個 unique factorization domain, 則 R[x1,..., xn] 這個 n 個變數的 polynomial ring 也是一個 unique factorization domain.

証 明. 利用數學歸納法, 當 n = 1 時 Theorem 8.4.15 告訴我們 R[x1] 是一個 integral domain. 假設 n - 1 時, R' = R[x1,..., xn - 1] 是 unique factorization domain. 再由 Theorem 8.4.15 知 R'[xn] = R[x1,..., xn] 也是 unique factorization domain. $ \qedsymbol$

Theorem 8.4.16 是一個代數上很重要的定理, 最常見的狀況是當 F 是一個 field 時因 F[x1] 是一個 unique factorization domain, 故知 F[x1,..., xn] 也是一個 unique factorization domain.

next up previous
下一頁: FIELD 上一頁: Unique Factorization Domain 前一頁: Unique factorization domain 的基本性質
Administrator 2005-06-18