

下一頁: Congruences
上一頁: Arithmetic Function
前一頁: Convolution
前面在介紹 Euler's  -function 時, 我們曾提及不容易找到
arithmetic function f 將
-function 時, 我們曾提及不容易找到
arithmetic function f 將  -function 表成
-function 表成
 (n) =
(n) = 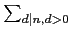 f (d ) 這樣的形式. 事實上 Möbius inversion
formula 可以幫助我們找到這樣的 f.
f (d ) 這樣的形式. 事實上 Möbius inversion
formula 可以幫助我們找到這樣的 f.
Theorem 2.5.1 (Möbius Inversion Formula)
假設
F,
f 皆為 arithmetic function,

為 möbius

-function. 則對任意
n 

,
F,
f 滿足
F(
n) =
 f
f (
d ),
若且唯若對任意
n 

,
F,
f 滿足
証 明.
令
l :

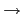

是一個 arithmetic function 滿足對任意
n 

,
l(
n) = 1. 依 convolution 的定義我們要證明
F =
f*
l 若且唯若
f =
F*

.
若
F = f*l, 則
F* = (f*l)*
= (f*l)* . 利用 Proposition
2.4.2(3) 知
F*
. 利用 Proposition
2.4.2(3) 知
F* = f*(l*
= f*(l* ). 然而對任意
n
). 然而對任意
n 
 ,
l*
,
l* (n) =
(n) =  *l(n) =
*l(n) = 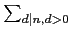
 (d ), 由 Example
2.1.6 知
l*
(d ), 由 Example
2.1.6 知
l* =
=  *l =
*l = 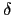 , 其中
, 其中
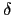 :
: 
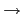
 定義為
定義為
換言之, 我們有
F*

=
f*(
l*

) =
f*
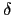
. 因而利用
Proposition
2.4.2(1) 得證
F*

=
f.
反之, 若 f = F* , 則
f*l = (F*
, 則
f*l = (F* )*l = F*(
)*l = F*( *l). 故再利用
*l). 故再利用
 *l =
*l = 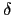 得知
f*l = F*
得知
f*l = F*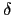 = F.
= F.
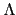
注意 Möbius inversion formula 需要對任意
n 
 對才能使用.
也就是說你不能看到
對才能使用.
也就是說你不能看到
F(6) = f (1) + f (2) + f (3) + f (6)
就下結論說
f (6) =
F(1)
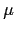
(6) +
F(2)
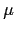
(3) +
F(3)
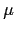
(2) +
F(6)
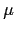
(1) =
F(1) -
F(2) -
F(3) +
F(6).
需要檢驗所有
n 
 都對才可下此結論 (至少在此例中還要多檢查
F(1) = f (1) ,
F(2) = f (1) + f (2) 以及
F(3) = f (1) + f (3)).
都對才可下此結論 (至少在此例中還要多檢查
F(1) = f (1) ,
F(2) = f (1) + f (2) 以及
F(3) = f (1) + f (3)).
Example 2.5.2
現在我們來看看如何利用 Möbius inversion formula, 找到
f 使得

(
n) =
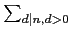 f
f (
d ). 由 Möbius inversion formula 知此時
f =

*

. 由於

和

皆為 multiplicative, 由 Theorem
2.4.3 知
f 亦為 multiplicative. 因此我們先觀察對任意質數
p 以及
t 

,
f (
pt) 之值. 然而
f (
pt) =
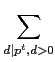
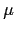
(
d )
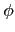
(
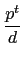
) =
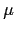
(1)
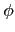
(
pt) +
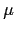
(
p)
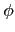
(
pt - 1) =
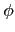
(
pt) -
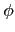
(
pt - 1).
因此知
f (
p) =
p - 1 - 1 =
p - 2 且當
t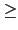
2 時
f (
pt) =
pt -
pt - 1 - (
pt - 1 -
pt - 2) =
pt - 2(
p - 1)
2. 因此若
n =
p1n1 ... prnr, 其中
pi 為相異質數, 可以得
f (
n) =
f (
p1n1)
... f (
prnr). 但是接下來很難將
f
寫成很好的形式 (注意要區分有某個
ni = 1 的情形). 事實上若沒有
Möbius inversion formula, 我們也很難證出這個
f 確實滿足

(
n) =
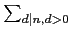 f
f (
d ). 所以當初在證明

是 multiplicative
時, 我們並沒有利用 Theorem
2.1.5 證得.
事實上利用 Example 2.5.2 的方法我們可以證出任何的 arithmetic
function F 皆可找到唯一的 arithmetic function f 使得對任意
n 
 , 皆有
F(n) =
, 皆有
F(n) = 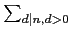 f (d ). 當我們找到的 f 是
multiplicative 時, Theorem 2.1.5 告訴我們 F 也是
multiplicative. 反之, 以下 Corollary 告訴我們若已知 F 是
multiplicative, 則找出的 f 一定也是 multiplicative.
f (d ). 當我們找到的 f 是
multiplicative 時, Theorem 2.1.5 告訴我們 F 也是
multiplicative. 反之, 以下 Corollary 告訴我們若已知 F 是
multiplicative, 則找出的 f 一定也是 multiplicative.
Corollary 2.5.3
假設
F,
f 皆為 arithmetic function.
若對任意
n 

, 皆有
F(
n) =
 f
f (
d )
且已知
F 是一個 multiplicative arithmetic
function, 則
f 亦為一個 multiplicative arithmetic function.
証 明.
由 Theorem
2.5.1 知
f =

*
F, 故由

是 multiplicative
以及
F 是 multiplicative 的假設, 利用 Theorem
2.4.3 知
f =

*
F 亦為 multiplicative.
Example 2.5.4
前面幾節中我們曾利用 multiplicative arithmetic function
得到一些有趣的等式, 接下來的例子我們將利用 Möbius inversion
formula 得到更多等式.
- 令 v(n) 表示 n 的正因數個數. 已知對任意
n

 ,
皆有
,
皆有
v(
n) =

1 =
 l
l(
d ),
其中對所有
n 
 ,
l(n) = 1, 故利用 Möbius inversion formula 知對任意
n
,
l(n) = 1, 故利用 Möbius inversion formula 知對任意
n 
 ,
,
1 =
l(
n) =

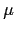
(
d )
v(
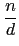
) =
 v
v(
d )
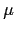
(
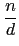
).
- 令
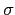 (n) 表示 n 的所有正因數之和. 已知對任意
n
(n) 表示 n 的所有正因數之和. 已知對任意
n 
 皆有
其中對所有
n
皆有
其中對所有
n 
 ,
,
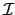 (n) = n, 故利用 Möbius inversion formula 知對任意
n
(n) = n, 故利用 Möbius inversion formula 知對任意
n 
 ,
,
n =
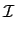
(
n) =

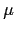
(
d )
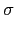
(
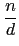
) =

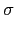
(
d )
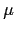
(
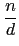
).
- 由 Corollary 2.3.6 知對任意
n

 皆有
故利用 Möbius inversion formula
知對任意
n
皆有
故利用 Möbius inversion formula
知對任意
n 
 , 皆有
, 皆有
Example 2.5.4(3) 的等式在前一節 Example 2.4.4
中我們曾用 multiplicative 的性質得到. 事實上 Example 2.5.4
中的等式都可以用 multiplicative 的性質得到. 不過要注意的是
Möbius inversion formula 並不侷限於 multiplicative 的情形, 它對
一般的 arithmetic function 皆適用.


下一頁: Congruences
上一頁: Arithmetic Function
前一頁: Convolution
Li
2007-06-28
 f (d ),
f (d ),
 F(d )
F(d ) f (d ),
f (d ),
 F(d )
F(d )![]() = (f*l)*
= (f*l)*![]() . 利用 Proposition
2.4.2(3) 知
F*
. 利用 Proposition
2.4.2(3) 知
F*![]() = f*(l*
= f*(l*![]() ). 然而對任意
n
). 然而對任意
n ![]()
![]() ,
l*
,
l*![]() (n) =
(n) = ![]() *l(n) =
*l(n) = ![]()
![]() (d ), 由 Example
2.1.6 知
l*
(d ), 由 Example
2.1.6 知
l*![]() =
= ![]() *l =
*l = ![]() , 其中
, 其中
![]() :
: ![]()
![]()
![]() 定義為
定義為
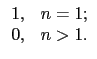
![]() , 則
f*l = (F*
, 則
f*l = (F*![]() )*l = F*(
)*l = F*(![]() *l). 故再利用
*l). 故再利用
![]() *l =
*l = ![]() 得知
f*l = F*
得知
f*l = F*![]() = F.
= F.
![]()
![]()
![]() 對才能使用.
也就是說你不能看到
對才能使用.
也就是說你不能看到
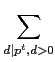
![]()
![]() , 皆有
F(n) =
, 皆有
F(n) = ![]() f (d ). 當我們找到的 f 是
multiplicative 時, Theorem 2.1.5 告訴我們 F 也是
multiplicative. 反之, 以下 Corollary 告訴我們若已知 F 是
multiplicative, 則找出的 f 一定也是 multiplicative.
f (d ). 當我們找到的 f 是
multiplicative 時, Theorem 2.1.5 告訴我們 F 也是
multiplicative. 反之, 以下 Corollary 告訴我們若已知 F 是
multiplicative, 則找出的 f 一定也是 multiplicative.
 f (d )
f (d )
 1 =
1 =  l(d ),
l(d ),

 v(d )
v(d ) d =
d = 




