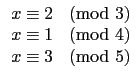

下一頁: 二次的 Congruence Equations
上一頁: Congruence Equations
前一頁: 一次的 Congruence Equations
假設
m = p1n1 ... prnr 其中 pi 為相異質數且 f (x)
是一個整係數多項式. Proposition 4.2.3 告訴我們若對所有
i  {1,..., r},
f (x)
{1,..., r},
f (x)  0(mod pini)
皆有解且有共同解, 則
f (x)
0(mod pini)
皆有解且有共同解, 則
f (x)  0(mod m) 便有解.
如何找到共同解呢? 中國剩餘定理 (Chinese Remainder Theorem)
告訴我們只要個別地將
f (x)
0(mod m) 便有解.
如何找到共同解呢? 中國剩餘定理 (Chinese Remainder Theorem)
告訴我們只要個別地將
f (x)  0(mod pini) 的解找到,
就可得到共同解.
0(mod pini) 的解找到,
就可得到共同解.
Theorem 4.4.1 (Chinese Remainder Theorem)
給定一組
m1,...,
mr 

其中這些
mi 皆兩兩互質 (即當
i j
j 時,
gcd(
mi,
mj) = 1). 則對任意的一組
c1,...,
cr 

皆可找到一整數
c 使得
c  ci
ci(mod
mi),
 i
i 
{1,...,
r}.
証 明.
為了方便, 我們令
M =
m1 ... mr 且對任意
i 
{1,...,
r}, 令
Mi =
M/
mi.
要注意這裡 Mj 和 mi 有以下的關係: (1) 若 i j, 則
mi| Mj. (2)
gcd(Mi, mi) = 1. 這裡 (1) 由 Mj
的定義相信大家很容易得知, 至於 (2) 不失一般性 (變換一下 mi
的順序), 我們僅需證明
gcd(M1, m1) = 1. 假設 M1, m1 不互質,
即存在一質數 p 使得 p| M1 且 p| m1. 然而依定義
M1 = m2 ... mr, 故由 Corollary 1.4.3 知存在
i
j, 則
mi| Mj. (2)
gcd(Mi, mi) = 1. 這裡 (1) 由 Mj
的定義相信大家很容易得知, 至於 (2) 不失一般性 (變換一下 mi
的順序), 我們僅需證明
gcd(M1, m1) = 1. 假設 M1, m1 不互質,
即存在一質數 p 使得 p| M1 且 p| m1. 然而依定義
M1 = m2 ... mr, 故由 Corollary 1.4.3 知存在
i  {2,..., r} 使得
p| mi. 但是 i
{2,..., r} 使得
p| mi. 但是 i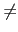 1, 依假設
gcd(m1, mi) = 1, 故 p| m1 且
p| mi 和 m1, mi 互質相矛盾, 故得證
gcd(M1, m1) = 1.
1, 依假設
gcd(m1, mi) = 1, 故 p| m1 且
p| mi 和 m1, mi 互質相矛盾, 故得證
gcd(M1, m1) = 1.
接下來我們想要找到一組
t1,..., tr 
 使得對所有的
i
使得對所有的
i  {1,..., r},
{1,..., r},
t = c1M1t1 + ... + crMrtr
皆滿足
t  ci
ci(mod
mi). 然而對任何的一組
t1,...,
tr 

以及一給定的
i 
{1,...,
r}, 由 (1) (即
mi|
Mj for
i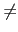 j
j)
我們皆有
t  ciMiti
ciMiti(mod
mi). 故我們僅需找到
ti 

使得
ciMiti  ci
ci(mod
mi) 即可. 然而由 (2) (即
gcd(
Mi,
mi) = 1) 以及 Proposition
3.2.5 知存在
ei 

使得
Miei 
1(mod
mi), 故若令
ti =
ei, 則得
t  ciMiei
ciMiei  ci
ci(mod
mi). 因此對所有
i 
{1,...,
r},
我們先找到
ei 使得
Miei 
1(mod
mi), 再令
c =
c1M1e1 +
... +
crMrer, 則可得
c  ci
ci(mod
mi),
 i
i 
{1,...,
r}.

要注意! 當這些 mi 不是兩兩互質時, 給定任意的
c1,..., cr
不見得可找到一個整數 c 使得
c  ci(mod mi) 對所有的
i
ci(mod mi) 對所有的
i  {1,..., r} 都成立. 例如當 m1 = 4, m2 = 6 時若考慮
c1 = 1, c2 = 2, 則不可能找到一整數 c 同時滿足
c
{1,..., r} 都成立. 例如當 m1 = 4, m2 = 6 時若考慮
c1 = 1, c2 = 2, 則不可能找到一整數 c 同時滿足
c  1(mod 4) 且
c
1(mod 4) 且
c  2(mod 6). 這是因為若
c
2(mod 6). 這是因為若
c  1(mod 4)
表示 c 為 4k + 1 的形式, 故必為奇數. 然而若
c
1(mod 4)
表示 c 為 4k + 1 的形式, 故必為奇數. 然而若
c  2(mod 6),
則 c 為 6k + 2 之形式, 必為偶數.
因此當然不可能找到一整數是奇數又是偶數.
2(mod 6),
則 c 為 6k + 2 之形式, 必為偶數.
因此當然不可能找到一整數是奇數又是偶數.
一般來說我們可以將中國剩餘定理看成是解如
這樣的聯立方程式.
一般來說聯立方程式是要找到一個共同解同時符合這 r
個式子感覺起來較難. 而在 Theorem 4.4.1 的證明中,
大家可以看出參數
t1,...tr 的設定, 就是要把這 r
個聯立的式子化成 r 個獨立的式子個別解出 ti 來, 自然就變簡單了.
我們來看看以下的例子.
Example 4.4.2
給定
m1 = 3,
m2 = 4,
m3 = 5 以及
c1 = 2,
c2 = 1,
c3 = 3
我們希望找到一整數
c 使得
c  ci
ci(mod
mi),
 i
i 
{1, 2, 3}. 也就是說找到
c 同時滿足
依照 Theorem
4.4.1 的符號訂法我們有
M1 = 20,
M2 = 15
以及
M3 = 12. 首先我們找到
e1 

使得
M1e1 
1(mod
m1), 即
20
e1 
1(mod 3), 也就是說滿足
2
e1 
1(mod 3). 由此找到
e1 = 2. 同理我們要找到
e2,
e3 分別滿足
15
e2 
1(mod 4) (即
3
e2 
1(mod 4)) 以及
12
e3 
1(mod 5) (即
2
e3 
1(mod 5)). 可得
e2 = 3 和
e3 = 3 分別滿足上式. 故令
c = 2×20×2 + 1×15×3 + 3×12×3 = 233 滿足
233

2(mod 3),
233

1(mod 4) 以及
233

3(mod 5).
前面提過, 給定
m 
 , 假設
m = p1n1 ... prnr, 其中
pi 為相異質數. 如果 f (x) 是一個整係數多項式, 要解
f (x)
, 假設
m = p1n1 ... prnr, 其中
pi 為相異質數. 如果 f (x) 是一個整係數多項式, 要解
f (x)  0(mod m), 我們可以先對每個 pi 考慮解
f (x)
0(mod m), 我們可以先對每個 pi 考慮解
f (x)  0(mod pini). 如果有一個 pi 發生
f (x)
0(mod pini). 如果有一個 pi 發生
f (x)  0(mod pini) 無解的情況, 那麼依 Proposition 4.2.3 知
f (x)
0(mod pini) 無解的情況, 那麼依 Proposition 4.2.3 知
f (x)  0(mod m) 無解. 如果每一個 pi 皆會使得
f (x)
0(mod m) 無解. 如果每一個 pi 皆會使得
f (x)  0(mod pini), 則依 Proposition 4.2.3 知, 需解聯立方程式
0(mod pini), 則依 Proposition 4.2.3 知, 需解聯立方程式
有一共同解才可得
f (x)  0(mod m) 的解.
解聯立方程是困難的, 而中國剩餘定理告訴我們可以不必考慮解聯立式子,
先個別將解求出便可得到共同的解.
0(mod m) 的解.
解聯立方程是困難的, 而中國剩餘定理告訴我們可以不必考慮解聯立式子,
先個別將解求出便可得到共同的解.
Corollary 4.4.3
假設
m =
p1n1 ... prnr, 其中這些
pi 為相異質數且
f (
x) 為一整係數多項式. 則對任意
i 
{1,...,
r},
f (
x)

0(mod
pini) 皆有解若且唯若
f (
x)

0(mod
m) 有解.
証 明.
依 Proposition
4.2.3 知, 如果
f (
x)

0(mod
m) 有解,
則對任意
i 
{1,...,
r},
f (
x)

0(mod
pini) 皆有解.
現假設對任意
i  {1,..., r},
f (x)
{1,..., r},
f (x)  0(mod pini)
皆有解且
x
0(mod pini)
皆有解且
x  ci(mod pini) 為其一解. 由於這些
pini 是兩兩互質的故依 Theorem 4.4.1 知, 存在
c
ci(mod pini) 為其一解. 由於這些
pini 是兩兩互質的故依 Theorem 4.4.1 知, 存在
c 
 滿足對任意
i
滿足對任意
i  {1,..., r} 皆有
c
{1,..., r} 皆有
c  ci(mod pini).
也就是說任意
i
ci(mod pini).
也就是說任意
i  {1,..., r},
x
{1,..., r},
x  c(mod pini) 為
f (x)
c(mod pini) 為
f (x)  0(mod pini) 之一解. 故再利用 Proposition
4.2.3 得知
x
0(mod pini) 之一解. 故再利用 Proposition
4.2.3 得知
x  c(mod m) 為
f (x)
c(mod m) 為
f (x)  0(mod m)
之一解.
0(mod m)
之一解.

我們就來看一個這方面的簡單例子.
雖然底下的例子可以直接代數字得到解答,
但是我們只是希望利用此例來講解這裡所用的概念,
所以希望大家了解應著重於如何應用所學的方法而不在於解答為何.
Example 4.4.4
我們來解
x2 
1(mod 15). 依前面結果知我們可以分別考慮
x2 
1(mod 3) 及
x2 
1(mod 5) 的解. 因為 3 和 5
皆為質數, 依 Lemma
3.4.2 知
x 
±1(mod 3) 和
x 
±1(mod 5) 分別為
x2 
1(mod 3) 和
x2 
1(mod 5)
之解. 因此我們要找到以下的四個聯立的 congruence equation:
(1) 和 (2) 我們很容易看出分別取整數 1 和 -1
就可分別滿足 (1) 和 (2). 而 11 可以滿足 (3), 4 可以滿足 (4).
所以由 Proposition
4.2.3 我們知
x 
1, - 1, 11, 4(mod 15)
都為
x2 
1(mod 15) 的解. 我們找到
x2 
1(mod 15) 在
modulo 15 之下的 4 個解, 並不表示就只有這 4 個解.
不過大家可以自行驗證一下在 modulo 15 之下確實僅有這 4 個解.
在上個例子中我們解出
x2  1(mod 15) 在 modulo 15 之下的
4 個解但不敢確定是否僅有這 4
解是因為我們不知在利用中國剩餘定理時, 是否還有其他的解. 也就是說
Theorem 4.4.1 只告訴我們解的存在性, 並未告訴我們是否有其他解.
當然我們都知道會有無窮多解, 但是其他的解如何得知呢?
我們再套用一次常用的老方法, 看看兩個解之間的關係為何,
自然就可將所有的解寫下了.
1(mod 15) 在 modulo 15 之下的
4 個解但不敢確定是否僅有這 4
解是因為我們不知在利用中國剩餘定理時, 是否還有其他的解. 也就是說
Theorem 4.4.1 只告訴我們解的存在性, 並未告訴我們是否有其他解.
當然我們都知道會有無窮多解, 但是其他的解如何得知呢?
我們再套用一次常用的老方法, 看看兩個解之間的關係為何,
自然就可將所有的解寫下了.
Theorem 4.4.5
給定一組
m1,...,
mr 

其中這些
mi 皆兩兩互質. 令
M =
m1 ... mr, 則對任意的一組
c1,...,
cr 

以下聯立的
congruence equation
在 modulo
M 之下存在唯一的一個解. 事實上若
c 

滿足此聯立 congruence equation, 則對任意
c' 

滿足
c'  c
c(mod
M) 皆會滿足此聯立 congruence equation.
証 明.
Theorem
4.4.1 已證得存在性, 我們要證明在 modulo
m1 ... mr
之下其解唯一.
假設
c, c' 
 皆滿足以上聯立的 congruence equation.
也就是說對任意
i
皆滿足以上聯立的 congruence equation.
也就是說對任意
i  {1,..., r} 我們皆有
c
{1,..., r} 我們皆有
c  ci(mod mi)
且
c'
ci(mod mi)
且
c'  ci(mod mi). 因此之對任意
i
ci(mod mi). 因此之對任意
i  {1,..., r} 皆有
mi| c - c'. 然而這些 mi 兩兩互質, 故利用 Proposition
1.2.11(2), 我們得
m1 ... mr| c - c', 即
c
{1,..., r} 皆有
mi| c - c'. 然而這些 mi 兩兩互質, 故利用 Proposition
1.2.11(2), 我們得
m1 ... mr| c - c', 即
c  c'(mod M).
也就是說在 modulo M 之下其解唯一.
c'(mod M).
也就是說在 modulo M 之下其解唯一.
另一方面, 若 c 滿足聯立 congruence equation 且
c' 
 滿足
c'
滿足
c'  c(mod M), 則由於對任意
i
c(mod M), 則由於對任意
i  {1,..., r}, mi| M,
故知
c'
{1,..., r}, mi| M,
故知
c'  c
c  ci(mod mi). 亦即 c' 滿足此聯立
congruence equation.
ci(mod mi). 亦即 c' 滿足此聯立
congruence equation.

例如在 Example 4.4.2 中, 我們知道 x = 233 滿足
這一組聯立的 congruence equation, 所以由 Theorem
4.4.5 知任意的整數 c 滿足
c  233
233  53(mod 60)
都可以滿足這一組聯立 congruence equation. 當然了也僅有滿足
c
53(mod 60)
都可以滿足這一組聯立 congruence equation. 當然了也僅有滿足
c  53(mod 60) 的整數會滿足此聯立 congruence equation.
53(mod 60) 的整數會滿足此聯立 congruence equation.
Theorem 4.4.5 比 Theorem 4.4.1 完整. 因為在 Theorem
4.4.1 中我們僅提及解的存在性, 而 Theorem 4.4.5 提及解在
modulo
m1 ... mr 之下是存在且唯一的,
而且因而可由一解找到所有的解. 有的書不會將兩定理分開來談,
而直接談論較完整的 Theorem 4.4.5 並稱之為 Chinese remainder
theorem.
我們將兩定理分開主要是因為想先強調中國剩餘定理解的存在性及如何找到一解.


下一頁: 二次的 Congruence Equations
上一頁: Congruence Equations
前一頁: 一次的 Congruence Equations
Li
2007-06-28
![]() j, 則
mi| Mj. (2)
gcd(Mi, mi) = 1. 這裡 (1) 由 Mj
的定義相信大家很容易得知, 至於 (2) 不失一般性 (變換一下 mi
的順序), 我們僅需證明
gcd(M1, m1) = 1. 假設 M1, m1 不互質,
即存在一質數 p 使得 p| M1 且 p| m1. 然而依定義
M1 = m2 ... mr, 故由 Corollary 1.4.3 知存在
i
j, 則
mi| Mj. (2)
gcd(Mi, mi) = 1. 這裡 (1) 由 Mj
的定義相信大家很容易得知, 至於 (2) 不失一般性 (變換一下 mi
的順序), 我們僅需證明
gcd(M1, m1) = 1. 假設 M1, m1 不互質,
即存在一質數 p 使得 p| M1 且 p| m1. 然而依定義
M1 = m2 ... mr, 故由 Corollary 1.4.3 知存在
i ![]() {2,..., r} 使得
p| mi. 但是 i
{2,..., r} 使得
p| mi. 但是 i![]() 1, 依假設
gcd(m1, mi) = 1, 故 p| m1 且
p| mi 和 m1, mi 互質相矛盾, 故得證
gcd(M1, m1) = 1.
1, 依假設
gcd(m1, mi) = 1, 故 p| m1 且
p| mi 和 m1, mi 互質相矛盾, 故得證
gcd(M1, m1) = 1.
![]()
![]() 使得對所有的
i
使得對所有的
i ![]() {1,..., r},
{1,..., r},
![]() ci(mod mi) 對所有的
i
ci(mod mi) 對所有的
i ![]() {1,..., r} 都成立. 例如當 m1 = 4, m2 = 6 時若考慮
c1 = 1, c2 = 2, 則不可能找到一整數 c 同時滿足
c
{1,..., r} 都成立. 例如當 m1 = 4, m2 = 6 時若考慮
c1 = 1, c2 = 2, 則不可能找到一整數 c 同時滿足
c ![]() 1(mod 4) 且
c
1(mod 4) 且
c ![]() 2(mod 6). 這是因為若
c
2(mod 6). 這是因為若
c ![]() 1(mod 4)
表示 c 為 4k + 1 的形式, 故必為奇數. 然而若
c
1(mod 4)
表示 c 為 4k + 1 的形式, 故必為奇數. 然而若
c ![]() 2(mod 6),
則 c 為 6k + 2 之形式, 必為偶數.
因此當然不可能找到一整數是奇數又是偶數.
2(mod 6),
則 c 為 6k + 2 之形式, 必為偶數.
因此當然不可能找到一整數是奇數又是偶數.
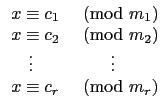

![]()
![]() , 假設
m = p1n1 ... prnr, 其中
pi 為相異質數. 如果 f (x) 是一個整係數多項式, 要解
f (x)
, 假設
m = p1n1 ... prnr, 其中
pi 為相異質數. 如果 f (x) 是一個整係數多項式, 要解
f (x) ![]() 0(mod m), 我們可以先對每個 pi 考慮解
f (x)
0(mod m), 我們可以先對每個 pi 考慮解
f (x) ![]() 0(mod pini). 如果有一個 pi 發生
f (x)
0(mod pini). 如果有一個 pi 發生
f (x) ![]() 0(mod pini) 無解的情況, 那麼依 Proposition 4.2.3 知
f (x)
0(mod pini) 無解的情況, 那麼依 Proposition 4.2.3 知
f (x) ![]() 0(mod m) 無解. 如果每一個 pi 皆會使得
f (x)
0(mod m) 無解. 如果每一個 pi 皆會使得
f (x) ![]() 0(mod pini), 則依 Proposition 4.2.3 知, 需解聯立方程式
0(mod pini), 則依 Proposition 4.2.3 知, 需解聯立方程式

![]() {1,..., r},
f (x)
{1,..., r},
f (x) ![]() 0(mod pini)
皆有解且
x
0(mod pini)
皆有解且
x ![]() ci(mod pini) 為其一解. 由於這些
pini 是兩兩互質的故依 Theorem 4.4.1 知, 存在
c
ci(mod pini) 為其一解. 由於這些
pini 是兩兩互質的故依 Theorem 4.4.1 知, 存在
c ![]()
![]() 滿足對任意
i
滿足對任意
i ![]() {1,..., r} 皆有
c
{1,..., r} 皆有
c ![]() ci(mod pini).
也就是說任意
i
ci(mod pini).
也就是說任意
i ![]() {1,..., r},
x
{1,..., r},
x ![]() c(mod pini) 為
f (x)
c(mod pini) 為
f (x) ![]() 0(mod pini) 之一解. 故再利用 Proposition
4.2.3 得知
x
0(mod pini) 之一解. 故再利用 Proposition
4.2.3 得知
x ![]() c(mod m) 為
f (x)
c(mod m) 為
f (x) ![]() 0(mod m)
之一解.
0(mod m)
之一解.
![]()
 , (2)
, (2)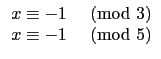 ,
,
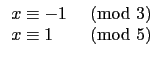 , (4)
, (4) .
.
![]() 1(mod 15) 在 modulo 15 之下的
4 個解但不敢確定是否僅有這 4
解是因為我們不知在利用中國剩餘定理時, 是否還有其他的解. 也就是說
Theorem 4.4.1 只告訴我們解的存在性, 並未告訴我們是否有其他解.
當然我們都知道會有無窮多解, 但是其他的解如何得知呢?
我們再套用一次常用的老方法, 看看兩個解之間的關係為何,
自然就可將所有的解寫下了.
1(mod 15) 在 modulo 15 之下的
4 個解但不敢確定是否僅有這 4
解是因為我們不知在利用中國剩餘定理時, 是否還有其他的解. 也就是說
Theorem 4.4.1 只告訴我們解的存在性, 並未告訴我們是否有其他解.
當然我們都知道會有無窮多解, 但是其他的解如何得知呢?
我們再套用一次常用的老方法, 看看兩個解之間的關係為何,
自然就可將所有的解寫下了.
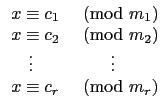
![]()
![]() 皆滿足以上聯立的 congruence equation.
也就是說對任意
i
皆滿足以上聯立的 congruence equation.
也就是說對任意
i ![]() {1,..., r} 我們皆有
c
{1,..., r} 我們皆有
c ![]() ci(mod mi)
且
c'
ci(mod mi)
且
c' ![]() ci(mod mi). 因此之對任意
i
ci(mod mi). 因此之對任意
i ![]() {1,..., r} 皆有
mi| c - c'. 然而這些 mi 兩兩互質, 故利用 Proposition
1.2.11(2), 我們得
m1 ... mr| c - c', 即
c
{1,..., r} 皆有
mi| c - c'. 然而這些 mi 兩兩互質, 故利用 Proposition
1.2.11(2), 我們得
m1 ... mr| c - c', 即
c ![]() c'(mod M).
也就是說在 modulo M 之下其解唯一.
c'(mod M).
也就是說在 modulo M 之下其解唯一.
![]()
![]() 滿足
c'
滿足
c' ![]() c(mod M), 則由於對任意
i
c(mod M), 則由於對任意
i ![]() {1,..., r}, mi| M,
故知
c'
{1,..., r}, mi| M,
故知
c' ![]() c
c ![]() ci(mod mi). 亦即 c' 滿足此聯立
congruence equation.
ci(mod mi). 亦即 c' 滿足此聯立
congruence equation.
![]()