我們還是要用 Euler's criterion 的精神來求
![]()
![]()
![]() 而不是直接探討
x2
而不是直接探討
x2 ![]() 2(mod p) 何時有解. 然而 Euler's
criterion 並不能直接套用來求
2(mod p) 何時有解. 然而 Euler's
criterion 並不能直接套用來求
![]()
![]()
![]() , 主要原因是我們這裡的 p
是一般的奇質數而不是特定的奇質數, 所以根本無法估計
2(p - 1)/2 在
modulo p 之下為 1 或 -1.
我們必須推導出另外的方法可以幫助我們求
2(p - 1)/2 在 modulo p
之情形.
, 主要原因是我們這裡的 p
是一般的奇質數而不是特定的奇質數, 所以根本無法估計
2(p - 1)/2 在
modulo p 之下為 1 或 -1.
我們必須推導出另外的方法可以幫助我們求
2(p - 1)/2 在 modulo p
之情形.
要證明
T = {1, 2,...,(p - 1)/2}. 我們先證明
T ![]() {1, 2,...,(p - 1)/2}. 然而對任意的
i
{1, 2,...,(p - 1)/2}. 然而對任意的
i ![]() {1,..., n}
我們有
p - ri
{1,..., n}
我們有
p - ri![]() p - (p + 1)/2 = (p - 1)/2 且
p - ri
p - (p + 1)/2 = (p - 1)/2 且
p - ri![]() p - (p - 1) = 1, 故知
p - ri
p - (p - 1) = 1, 故知
p - ri ![]() {1, 2,...,(p - 1)/2}. 另一方面對任意
j
{1, 2,...,(p - 1)/2}. 另一方面對任意
j ![]() {1,..., m}
已知
1
{1,..., m}
已知
1![]() sj
sj![]() (p - 1)/2 故得證
T
(p - 1)/2 故得證
T ![]() {1, 2,...,(p - 1)/2}.
{1, 2,...,(p - 1)/2}.
接下來我們證明 p - ri,
i ![]() {1,..., n} 和 sj,
j
{1,..., n} 和 sj,
j ![]() {1,..., m} 這 n + m (即 (p - 1)/2) 個元素皆相異, 便可得證
T = {1, 2,...,(p - 1)/2}. 所以我們要證明 (1):
1
{1,..., m} 這 n + m (即 (p - 1)/2) 個元素皆相異, 便可得證
T = {1, 2,...,(p - 1)/2}. 所以我們要證明 (1):
1![]() i
i![]() i'
i'![]() n
時,
p - ri
n
時,
p - ri![]() p - ri'; (2):
1
p - ri'; (2):
1![]() j
j![]() j'
j'![]() m 時,
sj
m 時,
sj![]() sj' 以及 (3): 對任意
i
sj' 以及 (3): 對任意
i ![]() {1,..., n},
j
{1,..., n},
j ![]() {1,..., m},
p - ri
{1,..., m},
p - ri![]() sj.
sj.
當
1![]() i
i![]() i'
i'![]() n 時, 若
p - ri = p - ri' 表示
ri = ri',
依定義即 nia 和 ni'a 除以 p 的餘數相同, 也就是說
nia
n 時, 若
p - ri = p - ri' 表示
ri = ri',
依定義即 nia 和 ni'a 除以 p 的餘數相同, 也就是說
nia ![]() ni'a(mod p). 然而已假設 a 和 p 互質故由
Corollary 3.2.4 知
ni
ni'a(mod p). 然而已假設 a 和 p 互質故由
Corollary 3.2.4 知
ni ![]() ni'(mod p). 但此與
1
ni'(mod p). 但此與
1![]() ni
ni![]() ni'
ni'![]() (p - 1)/2 的假設矛盾, 故得證
p - ri
(p - 1)/2 的假設矛盾, 故得證
p - ri![]() p - ri', 即
(1) 是對的. 同理可證得 (2) 是對的. 至於 (3), 若 p - ri = sj, 表示
ri + sj = p, 可得
nia + mja
p - ri', 即
(1) 是對的. 同理可證得 (2) 是對的. 至於 (3), 若 p - ri = sj, 表示
ri + sj = p, 可得
nia + mja ![]() 0(mod p). 故再由 Corollary
3.2.4 得
ni + mj
0(mod p). 故再由 Corollary
3.2.4 得
ni + mj ![]() 0(mod p). 然而
1
0(mod p). 然而
1![]() ni, mj
ni, mj![]() (p - 1)/2, 得
2
(p - 1)/2, 得
2![]() ni + mj
ni + mj![]() p - 1, 不可能滿足 p| ni + mj, 故得證
p - ri
p - 1, 不可能滿足 p| ni + mj, 故得證
p - ri![]() sj.
sj.
既然 T = {1, 2,...,(p - 1)/2}, 我們得
若
{a, 2a,...,![]() a} 中共有 n 個元素除以 p
的餘數大於 (p - 1)/2, 則由 Corollary 5.3.4 以及 Lemma
5.4.2 知
a} 中共有 n 個元素除以 p
的餘數大於 (p - 1)/2, 則由 Corollary 5.3.4 以及 Lemma
5.4.2 知
Gauss's Lemma 將繁複
a(p - 1)/2 的計算換成計算
{a, 2a,...,![]() a} 中有多少個除以 p 的餘數大於
(p - 1)/2, 確實將問題簡化了. 我們可以利用它來計算
a} 中有多少個除以 p 的餘數大於
(p - 1)/2, 確實將問題簡化了. 我們可以利用它來計算
![]()
![]()
![]() .
.
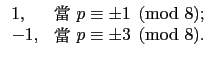
當 p = 8k + 1 (即
p ![]() 1(mod 8)) 時,
(p - 1)/2 = 4k. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k 且大於 4k
的偶數之個數. 知其共有
(8k - 4k)/2 = 2k. 故由 Corollary 5.3.4
以及 Lemma 5.4.2 知
1(mod 8)) 時,
(p - 1)/2 = 4k. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k 且大於 4k
的偶數之個數. 知其共有
(8k - 4k)/2 = 2k. 故由 Corollary 5.3.4
以及 Lemma 5.4.2 知
當 p = 8k - 1 (即
p ![]() - 1(mod 8)) 時,
(p - 1)/2 = 4k - 1. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k - 2 且大於 4k - 1
的偶數之個數. 知其共有
(8k - 2 - (4k - 2))/2 = 2k. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知
- 1(mod 8)) 時,
(p - 1)/2 = 4k - 1. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k - 2 且大於 4k - 1
的偶數之個數. 知其共有
(8k - 2 - (4k - 2))/2 = 2k. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知
當 p = 8k + 3 (即
p ![]() 3(mod 8)) 時,
(p - 1)/2 = 4k + 1. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k + 2 且大於 4k + 1
的偶數之個數. 知其共有
(8k + 2 - 4k)/2 = 2k + 1. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知
3(mod 8)) 時,
(p - 1)/2 = 4k + 1. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k + 2 且大於 4k + 1
的偶數之個數. 知其共有
(8k + 2 - 4k)/2 = 2k + 1. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知
當 p = 8k - 3 (即
p ![]() - 3(mod 8)) 時,
(p - 1)/2 = 4k - 2. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k - 4 且大於 4k - 2
的偶數之個數. 知其共有
(8k - 4 - (4k - 2))/2 = 2k - 1. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知
- 3(mod 8)) 時,
(p - 1)/2 = 4k - 2. 因此 S
中大於 (p - 1)/2 的元素個數即為小於等於 p - 1 = 8k - 4 且大於 4k - 2
的偶數之個數. 知其共有
(8k - 4 - (4k - 2))/2 = 2k - 1. 故由 Corollary
5.3.4 以及 Lemma 5.4.2 知