求 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$

最後我們來探討 p, q 為相異奇質數的情形. 若給定了 p 和 q 我們當然就可以利用 Gauss's Lemma 求 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$, 不過現在要討論的是一般的 p 和 q, 我們必須考慮別的方法.

在 Gauss's Lemma 中我們需要算出 {a, 2a,...,${\dfrac{p-1}{2}}$a} 中有多少元素其除以 p 的餘數大於 (p - 1)/2. 若其個數為 n, 則 $\left(\vphantom{\dfrac{{a}}{\,{p}\,}}\right.$${\dfrac{{a}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{a}}{\,{p}\,}}\right)$ = (- 1)ⁿ. 由於 (- 1)ⁿ 的取值完全取決於 n 是奇數或偶數, 所以我們並不需精確地算出 n 為多少, 只需確認其為奇數或偶數即可. 以下我們將介紹一個判別 n 為奇或偶的方法, 不過由於我們要考慮的 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 其中 q 為奇質數, 所以底下的方法中我們僅考慮 a 為奇數的情況.

為了方便我們先介紹一個符號. 給定一實數 r, 我們令 [r] 表示小於等於 r 的整數中最大的整數. 例如若 $\pi$ 表圓周率, 則 [$\pi$] = 3. 又例如 [- 5.2] = - 6. 要注意當 m, n 是正整數時 [m/n] 即為 m 除以 n 的商.

Lemma 5.4.4   給定一奇質數 p 及一奇數 a 滿足 p$\nmid$a. 若令 n 表示集合 {a, 2a,...,${\dfrac{p-1}{2}}$a} 中除以 p 餘數大於 (p - 1)/2 的元素個數, 則

n $$\equiv$$ $$\sum_{k=1}^{(p-1)/2}$$$$\left[\vphantom{\frac{ka}{p}}\right.$$$${\frac{ka}{p}}$$$$\left.\vphantom{\frac{ka}{p}}\right]$$(mod 2).

証 明. 假設 ka 除以 p 的餘數為 r, 則依定義我們有 ka = p[ka/p] + r. 故若依 Lemma 5.4.2 的證明我們將 {a, 2a, ^... ,${\dfrac{p-1}{2}}$a} 中的元素除以 p 的餘數分成 r₁,..., r_n 及 s₁,..., s_m 兩部份, 其中 r_i 是大於 (p - 1)/2 的部份, 而 s_j 表小於等於 (p - 1)/2 的部份, 則

$$\sum_{k=1}^{(p-1)/2}$$ka = $$\sum_{k=1}^{(p-1)/2}$$p$$\left[\vphantom{\frac{ka}{p}}\right.$$$${\frac{ka}{p}}$$$$\left.\vphantom{\frac{ka}{p}}\right]$$ + $$\sum_{i=1}^{n}$$r_i + $$\sum_{j=1}^{m}$$s_j.

由於我們僅在乎奇或偶, 所以可考慮上式在 modulo 2 的情況, 故利用 a 和 p 皆為奇數 (即 a $\equiv$ p $\equiv$ 1(mod 2)) 我們得

$$\sum_{k=1}^{(p-1)/2} \equiv \sum_{k=1}^{(p-1)/2} \left[\vphantom{\frac{ka}{p}}\right. {\frac{ka}{p}} \left.\vphantom{\frac{ka}{p}}\right] \sum_{i=1}^{n} \sum_{j=1}^{m}$$ (5.1)

另一方面在 Lemma 5.4.2 的證明中我們證得

{p - r₁,..., p - r_n, s₁,..., s_m} = {1, 2,...,(p - 1)/2}.

故得

$$\sum_{k=1}^{(p-1)/2}$$k = $$\sum_{i=1}^{n}$$(p - r_i) + $$\sum_{j=1}^{m}$$s_j = np - $$\sum_{i=1}^{n}$$r_i + $$\sum_{j=1}^{m}$$s_j.

再利用 p $\equiv$ 1(mod 2) 得

$$\sum_{k=1}^{(p-1)/2} \equiv \sum_{i=1}^{n} \sum_{j=1}^{m}$$ (5.2)

合併式子 (5.1) 和 (5.2) 得證

n $$\equiv$$ $$\sum_{k=1}^{(p-1)/2}$$$$\left[\vphantom{\frac{ka}{p}}\right.$$$${\frac{ka}{p}}$$$$\left.\vphantom{\frac{ka}{p}}\right]$$ + 2$$\sum_{i=1}^{n}$$r_i $$\equiv$$ $$\sum_{k=1}^{(p-1)/2}$$$$\left[\vphantom{\frac{ka}{p}}\right.$$$${\frac{ka}{p}}$$$$\left.\vphantom{\frac{ka}{p}}\right]$$(mod 2).

$\qedsymbol$

再次強調在 Lemma 5.4.4 的證明中我們用到 a 是奇數 (即 a $\equiv$ 1(mod 2)) 的假設, 所以此結果僅適用於 a 為奇數的情況, 千萬別用此法來算 $\left(\vphantom{\dfrac{{2}}{\,{p}\,}}\right.$${\dfrac{{2}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{2}}{\,{p}\,}}\right)$.

利用 Corollary 5.3.4 以及 Lemma 5.4.2, Lemma 5.4.4, 我們知給定一奇質數 p, 要計算一個奇數 a 其 $\left(\vphantom{\dfrac{{a}}{\,{p}\,}}\right.$${\dfrac{{a}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{a}}{\,{p}\,}}\right)$ 之值, 我們只要計算 $\sum_{k=1}^{(p-1)/2}$[ka/p] 之值即可. 若其值為 N, 則得 $\left(\vphantom{\dfrac{{a}}{\,{p}\,}}\right.$${\dfrac{{a}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{a}}{\,{p}\,}}\right)$ = (- 1)^N. 例如要求 $\left(\vphantom{\dfrac{{5}}{\,{11}\,}}\right.$${\dfrac{{5}}{\,{11}\,}}$$\left.\vphantom{\dfrac{{5}}{\,{11}\,}}\right)$, 我們只要計算 [5/11] + [10/11] + [15/11] + [20/11] + [25/11]. 算出其值為 4, 故知 $\left(\vphantom{\dfrac{{5}}{\,{11}\,}}\right.$${\dfrac{{5}}{\,{11}\,}}$$\left.\vphantom{\dfrac{{5}}{\,{11}\,}}\right)$ = (- 1)⁴ = 1.

接著我們要利用 Lemma 5.4.4 來計算 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$. 很容易理解算 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 不止和 p 有關也和 q 有關, 所以我們要探討 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 和 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ 的關係. 由於 p, q 皆為奇質數, 我們都可以利用 Lemma 5.4.4 來計算 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 和 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$. 因此我們要探討 $\sum_{k=1}^{(p-1)/2}$[kq/p] 和 $\sum_{l=1}^{(q-1)/2}$[lp/q] 之間的關係.

在探討此問題前, 我們再從另一個角度來看 [r] 這個整數. 當 r 是正的實數時, [r] 之值就是所有滿足 0$\le$n$\le$r 的正整數 n 的個數. 在座標 xy-平面上, 我們稱 x-軸及 y-軸座標皆為正整數的點為``正格子點''. 依此看法, 當 k 是正整數時, [kq/p] 之值就是直線 x = k 在 0$\le$y$\le$kq/p 之間的正格子點個數. 而當 l 是正整數時, [lp/q] 之值就是直線 y = l 在 0$\le$x$\le$lp/q 之間的正格子點個數. 利用這種觀點, 我們有以下之結果.

Lemma 5.4.5   假設 p 和 q 為相異奇質數. 則

$$\sum_{k=1}^{(p-1)/2}$$$$\left[\vphantom{\frac{kq}{p}}\right.$$$${\frac{kq}{p}}$$$$\left.\vphantom{\frac{kq}{p}}\right]$$ + $$\sum_{l=1}^{(q-1)/2}$$$$\left[\vphantom{\frac{lp}{q}}\right.$$$${\frac{lp}{q}}$$$$\left.\vphantom{\frac{lp}{q}}\right]$$ = $${\frac{p-1}{2}}$$$${\frac{q-1}{2}}$$.

証 明. 在 xy-平面上, 考慮以 (0, 0), (p/2, 0), (p/2, q/2) 以及 (0, q/2) 四點為頂點的長方形區域 T, 並以直線 L : y = (q/p)x 將此區域分成 T₁ 和 T₂ 兩部份. 其中 T₁ 表直線 L 下方的部份, 而 T₂ 表直線 L 上方的部份, 如下圖.

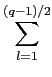
在 T 中的任意正格子點 (m, n), 依定義需滿足 m, n $\in$ $\mathbb {N}$ 且 0$\le$m$\le$p/2 及 0$\le$n$\le$q/2. 因此由 p, q 為奇數知在 T 中的正格子點個數為 ${\dfrac{p-1}{2}}$${\dfrac{q-1}{2}}$.

另一方面在 T₁ 中的正格子點 (k, s), 依定義需滿足 k, s $\in$ $\mathbb {N}$ 且 0$\le$k$\le$p/2 及 0$\le$s$\le$kq/p. 也就是說 k $\in$ $\mathbb {N}$ 需滿足 1$\le$k$\le$(p - 1)/2, 且給定 k, 則 0$\le$s$\le$kq/p. 換句話說要計算在 T₁ 中的格子點, 等於在計算給定 k $\in$ $\mathbb {N}$ 且 1$\le$k$\le$(p - 1)/2 時 會有多少 s $\in$ $\mathbb {N}$ 滿足 0$\le$s$\le$kq/p, 再將所有 k 所算得之結果加起來. 然而對任意的正整數 k 符合 0$\le$s$\le$kq/p 的正整數 s 的個數為 [kq/p]. 所以在 T₁ 中的正格子點數為 $\sum_{k=1}^{(p-1)/2}$[kq/p]. 同理在 T₂ 中的正格子點數為 $\sum_{l=1}^{(q-1)/2}$[lp/q].

在 T₁ 和 T₂ 的交界, 即滿足 y = (q/p)x 且 0$\le$x$\le$p/2 的線段上會不會有正格子點呢? 若 (m, n) 為其上之ㄧ正格子點, 則我們有 pn = qm 且 1$\le$m$\le$(p - 1)/2. 然而由 pn = qm 可得 p| qm, 再因 p, q 為相異質數故由 Proposition 1.2.7(1) 知 p| m, 此和 1$\le$m$\le$(p - 1)/2 相矛盾. 故知在 T₁ 和 T₂ 交界的線段上無正格子點. 因此在 T₁ 和 T₂ 上的正格子點數之和恰為在 T 上的正格子點數, 故得證

$$\sum_{k=1}^{(p-1)/2}$$$$\left[\vphantom{\frac{kq}{p}}\right.$$$${\frac{kq}{p}}$$$$\left.\vphantom{\frac{kq}{p}}\right]$$ + $$\sum_{l=1}^{(q-1)/2}$$$$\left[\vphantom{\frac{lp}{q}}\right.$$$${\frac{lp}{q}}$$$$\left.\vphantom{\frac{lp}{q}}\right]$$ = $${\frac{p-1}{2}}$$$${\frac{q-1}{2}}$$.

$\qedsymbol$

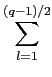
當 p, q 為相異奇質數, 若 M = $\sum_{k=1}^{(p-1)/2}$[kq/p] 且 N = $\sum_{l=1}^{(q-1)/2}$[lp/q] 由 Lemma 5.4.4 知 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ = (- 1)^M 且 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ = (- 1)^N. 而 Lemma 5.4.5 告訴我們 M + N = (p - 1)(q - 1)/4, 故得

$$\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$$$${\dfrac{{q}}{\,{p}\,}}$$$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$$$$\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$$$${\dfrac{{p}}{\,{q}\,}}$$$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$$ = (- 1)^{M + N} = (- 1)^{${\frac{p-1}{2}}$${\frac{q-1}{2}}$}.

因此我們有以下之結果.

Theorem 5.4.6 (Quadratic Reciprocity Law)   假設 p 和 q 為相異奇質數. 則

$$\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$$$${\dfrac{{q}}{\,{p}\,}}$$$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$$ = $$\left\{\vphantom{ \begin{array}{ll} -\left(\dfrac{{p}}{\,{q}\,}\... ...eft(\dfrac{{p}}{\,{q}\,}\right), & \hbox{其他情形.} \\ \end{array}%% }\right.$$$$\begin{array}{ll} -\left(\dfrac{{p}}{\,{q}\,}\right), & \hbox{若... ...$} \\ \left(\dfrac{{p}}{\,{q}\,}\right), & \hbox{其他情形.} \\ \end{array}$$

証 明. 由於 p, q 皆為奇數, 我們依 p $\equiv$ ±1(mod 4) 以及 q $\equiv$ ±1(mod 4) 四種情形來討論.

假設 p = 4k - 1 且 q = 4k' - 1 其中 k, k' $\in$ $\mathbb {N}$ (即 p $\equiv$ q $\equiv$ - 1(mod 4)). 則 (p - 1)/2 = 2k - 1 且 (q - 1)/2 = 2k' - 1, 故得

$$\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$$$${\dfrac{{q}}{\,{p}\,}}$$$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$$$$\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$$$${\dfrac{{p}}{\,{q}\,}}$$$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$$ = (- 1)^{(2k - 1)(2k' - 1)} = - 1.

也就是說 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ = - $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$.

剩下的情況為 p 和 q 中至少有一個在 modulo 4 之後餘 1. 不失一般性就假設 p $\equiv$ 1(mod 4). 此時 p = 4k + 1, 其中 k $\in$ $\mathbb {N}$, 故得 (p - 1)/2 = 2k. 而 (q - 1)/2 必為整數故知

$$\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$$$${\dfrac{{q}}{\,{p}\,}}$$$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$$$$\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$$$${\dfrac{{p}}{\,{q}\,}}$$$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$$ = (- 1)^{(2k)${\frac{q-1}{2}}$} = 1^{${\frac{q-1}{2}}$} = 1.

也就是說 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ = $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$. $\qedsymbol$

要注意 Theorem 5.4.6 要在 p, q 為相異奇質數時才適用, 否則若 q 不是奇質數, $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ 這個符號是沒有定義的. 雖然 Theorem 5.4.6 並沒有明確告訴我們 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 之值為何, 但是可利用 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ 之值來求得 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$. 一般來說將 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 的問題反轉成 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ 的問題就像輾轉相除法一樣, 可以快速的將問題簡化. 這是因為一般來說利用 Lemma 5.3.2(2), 要求 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 時, 可假設 q < p, 所以一反轉成 $\left(\vphantom{\dfrac{{p}}{\,{q}\,}}\right.$${\dfrac{{p}}{\,{q}\,}}$$\left.\vphantom{\dfrac{{p}}{\,{q}\,}}\right)$ 時我們已將一個 modulo 比較大的 p 的問題簡化成一個 modulo 比較小的 q 的問題. 例如求 $\left(\vphantom{\dfrac{{7}}{\,{101}\,}}\right.$${\dfrac{{7}}{\,{101}\,}}$$\left.\vphantom{\dfrac{{7}}{\,{101}\,}}\right)$, 由於 101 $\equiv$ 1(mod 4), 故得 $\left(\vphantom{\dfrac{{7}}{\,{101}\,}}\right.$${\dfrac{{7}}{\,{101}\,}}$$\left.\vphantom{\dfrac{{7}}{\,{101}\,}}\right)$ = $\left(\vphantom{\dfrac{{101}}{\,{7}\,}}\right.$${\dfrac{{101}}{\,{7}\,}}$$\left.\vphantom{\dfrac{{101}}{\,{7}\,}}\right)$. 所以馬上將 modulo 101 的問題轉成 modulo 7 的問題, 自然變得簡單. 事實上 $\left(\vphantom{\dfrac{{101}}{\,{7}\,}}\right.$${\dfrac{{101}}{\,{7}\,}}$$\left.\vphantom{\dfrac{{101}}{\,{7}\,}}\right)$ = $\left(\vphantom{\dfrac{{3}}{\,{7}\,}}\right.$${\dfrac{{3}}{\,{7}\,}}$$\left.\vphantom{\dfrac{{3}}{\,{7}\,}}\right)$, 可馬上驗證知 $\left(\vphantom{\dfrac{{3}}{\,{7}\,}}\right.$${\dfrac{{3}}{\,{7}\,}}$$\left.\vphantom{\dfrac{{3}}{\,{7}\,}}\right)$ = - 1 (或再用一次 Theorem 5.4.6 得 $\left(\vphantom{\dfrac{{3}}{\,{7}\,}}\right.$${\dfrac{{3}}{\,{7}\,}}$$\left.\vphantom{\dfrac{{3}}{\,{7}\,}}\right)$ = - $\left(\vphantom{\dfrac{{7}}{\,{3}\,}}\right.$${\dfrac{{7}}{\,{3}\,}}$$\left.\vphantom{\dfrac{{7}}{\,{3}\,}}\right)$ = - $\left(\vphantom{\dfrac{{1}}{\,{3}\,}}\right.$${\dfrac{{1}}{\,{3}\,}}$$\left.\vphantom{\dfrac{{1}}{\,{3}\,}}\right)$ = - 1). 所以得知 $\left(\vphantom{\dfrac{{7}}{\,{101}\,}}\right.$${\dfrac{{7}}{\,{101}\,}}$$\left.\vphantom{\dfrac{{7}}{\,{101}\,}}\right)$ = - 1. 總而言之, 對於一般的相異奇質數 p, q, 我們沒有辦法由 p 和 q 馬上得知 $\left(\vphantom{\dfrac{{q}}{\,{p}\,}}\right.$${\dfrac{{q}}{\,{p}\,}}$$\left.\vphantom{\dfrac{{q}}{\,{p}\,}}\right)$ 之值. 但是利用 Theorem 5.4.6, 我們可以很快速的將問題化簡而求出其值. 最後我們來看一個例子整合這一節中學到的方法.

Example 5.4.7   考慮二次 congruence equation x² $\equiv$ 539(mod 631) 是否有解. 要注意若要用 Legendre symbol 處理, 首先要檢查 631 是否為質數. 我們可以利用篩法 (Proposition 1.4.6) 檢查小於 $\sqrt{631}$ 的質數是否可整除 631. 由於小餘 25 的質數皆不能整除 631, 所以 Proposition 1.4.6 告訴我們 631 是質數. 因此我們就是要計算 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ 之值. 由於 539 和 631 頗近, 我們利用 539 $\equiv$ - 92(mod 631) 以及 Lemma 5.3.2(2) 知 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ = $\left(\vphantom{\dfrac{{-92}}{\,{631}\,}}\right.$${\dfrac{{-92}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{-92}}{\,{631}\,}}\right)$ 接著將 92 作質因數分解得 92 = 2²×23. 故利用 Proposition 5.3.5 知

$$\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$$$${\dfrac{{539}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{-92}}{\,{631}\,}}\right.$$$${\dfrac{{-92}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{-92}}{\,{631}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{-1}}{\,{631}\,}}\right.$$$${\dfrac{{-1}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{-1}}{\,{631}\,}}\right)$$$$\left(\vphantom{\dfrac{{4}}{\,{631}\,}}\right.$$$${\dfrac{{4}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{4}}{\,{631}\,}}\right)$$$$\left(\vphantom{\dfrac{{23}}{\,{631}\,}}\right.$$$${\dfrac{{23}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{23}}{\,{631}\,}}\right)$$.

由於 631 $\equiv$ 3 $\equiv$ - 1(mod 4), 故由 Theorem 5.4.1 知 $\left(\vphantom{\dfrac{{-1}}{\,{631}\,}}\right.$${\dfrac{{-1}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{-1}}{\,{631}\,}}\right)$ = - 1. 而 4 = 2², 故由 Lemma 5.3.2(1) 知 $\left(\vphantom{\dfrac{{4}}{\,{631}\,}}\right.$${\dfrac{{4}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{4}}{\,{631}\,}}\right)$ = 1, 因此得 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ = - $\left(\vphantom{\dfrac{{23}}{\,{631}\,}}\right.$${\dfrac{{23}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{23}}{\,{631}\,}}\right)$. 由於 631 $\equiv$ 23 $\equiv$ 3(mod 4), 故由 Theorem 5.4.6 知 $\left(\vphantom{\dfrac{{23}}{\,{631}\,}}\right.$${\dfrac{{23}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{23}}{\,{631}\,}}\right)$ = - $\left(\vphantom{\dfrac{{631}}{\,{23}\,}}\right.$${\dfrac{{631}}{\,{23}\,}}$$\left.\vphantom{\dfrac{{631}}{\,{23}\,}}\right)$. 又由 631 $\equiv$ 10(mod 23) 因此知

$$\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$$$${\dfrac{{539}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$$ = - $$\left(\vphantom{\dfrac{{23}}{\,{631}\,}}\right.$$$${\dfrac{{23}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{23}}{\,{631}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{631}}{\,{23}\,}}\right.$$$${\dfrac{{631}}{\,{23}\,}}$$$$\left.\vphantom{\dfrac{{631}}{\,{23}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{10}}{\,{23}\,}}\right.$$$${\dfrac{{10}}{\,{23}\,}}$$$$\left.\vphantom{\dfrac{{10}}{\,{23}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{2}}{\,{23}\,}}\right.$$$${\dfrac{{2}}{\,{23}\,}}$$$$\left.\vphantom{\dfrac{{2}}{\,{23}\,}}\right)$$$$\left(\vphantom{\dfrac{{5}}{\,{23}\,}}\right.$$$${\dfrac{{5}}{\,{23}\,}}$$$$\left.\vphantom{\dfrac{{5}}{\,{23}\,}}\right)$$.

因為 23 $\equiv$ 7 $\equiv$ - 1(mod 8), 故由 Theorem 5.4.3 知 $\left(\vphantom{\dfrac{{2}}{\,{23}\,}}\right.$${\dfrac{{2}}{\,{23}\,}}$$\left.\vphantom{\dfrac{{2}}{\,{23}\,}}\right)$ = 1. 又因 5 $\equiv$ 1(mod 4), 故由 Theorem 5.4.6 知 $\left(\vphantom{\dfrac{{5}}{\,{23}\,}}\right.$${\dfrac{{5}}{\,{23}\,}}$$\left.\vphantom{\dfrac{{5}}{\,{23}\,}}\right)$ = $\left(\vphantom{\dfrac{{23}}{\,{5}\,}}\right.$${\dfrac{{23}}{\,{5}\,}}$$\left.\vphantom{\dfrac{{23}}{\,{5}\,}}\right)$. 因此得 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ = $\left(\vphantom{\dfrac{{2}}{\,{23}\,}}\right.$${\dfrac{{2}}{\,{23}\,}}$$\left.\vphantom{\dfrac{{2}}{\,{23}\,}}\right)$$\left(\vphantom{\dfrac{{5}}{\,{23}\,}}\right.$${\dfrac{{5}}{\,{23}\,}}$$\left.\vphantom{\dfrac{{5}}{\,{23}\,}}\right)$ = $\left(\vphantom{\dfrac{{23}}{\,{5}\,}}\right.$${\dfrac{{23}}{\,{5}\,}}$$\left.\vphantom{\dfrac{{23}}{\,{5}\,}}\right)$. 再由 23 $\equiv$ 3(mod 5) 以及 5 $\equiv$ 1(mod 4) 知 $\left(\vphantom{\dfrac{{23}}{\,{5}\,}}\right.$${\dfrac{{23}}{\,{5}\,}}$$\left.\vphantom{\dfrac{{23}}{\,{5}\,}}\right)$ = $\left(\vphantom{\dfrac{{3}}{\,{5}\,}}\right.$${\dfrac{{3}}{\,{5}\,}}$$\left.\vphantom{\dfrac{{3}}{\,{5}\,}}\right)$ = $\left(\vphantom{\dfrac{{5}}{\,{3}\,}}\right.$${\dfrac{{5}}{\,{3}\,}}$$\left.\vphantom{\dfrac{{5}}{\,{3}\,}}\right)$ = $\left(\vphantom{\dfrac{{2}}{\,{3}\,}}\right.$${\dfrac{{2}}{\,{3}\,}}$$\left.\vphantom{\dfrac{{2}}{\,{3}\,}}\right)$. 所以知 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ = $\left(\vphantom{\dfrac{{2}}{\,{3}\,}}\right.$${\dfrac{{2}}{\,{3}\,}}$$\left.\vphantom{\dfrac{{2}}{\,{3}\,}}\right)$ = - 1. 也就是說 x² $\equiv$ 539(mod 631) 無解.

當然了當初若看出 539 = 7²×11, 則馬上得 $\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$${\dfrac{{539}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$ = $\left(\vphantom{\dfrac{{7^2}}{\,{631}\,}}\right.$${\dfrac{{7^2}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{7^2}}{\,{631}\,}}\right)$$\left(\vphantom{\dfrac{{11}}{\,{631}\,}}\right.$${\dfrac{{11}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{11}}{\,{631}\,}}\right)$ = $\left(\vphantom{\dfrac{{11}}{\,{631}\,}}\right.$${\dfrac{{11}}{\,{631}\,}}$$\left.\vphantom{\dfrac{{11}}{\,{631}\,}}\right)$. 再因 631 $\equiv$ 11 $\equiv$ 3(mod 4) 以及 631 $\equiv$ 4(mod 11) 知

$$\left(\vphantom{\dfrac{{539}}{\,{631}\,}}\right.$$$${\dfrac{{539}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{539}}{\,{631}\,}}\right)$$ = $$\left(\vphantom{\dfrac{{11}}{\,{631}\,}}\right.$$$${\dfrac{{11}}{\,{631}\,}}$$$$\left.\vphantom{\dfrac{{11}}{\,{631}\,}}\right)$$ = - $$\left(\vphantom{\dfrac{{631}}{\,{11}\,}}\right.$$$${\dfrac{{631}}{\,{11}\,}}$$$$\left.\vphantom{\dfrac{{631}}{\,{11}\,}}\right)$$ = - $$\left(\vphantom{\dfrac{{4}}{\,{11}\,}}\right.$$$${\dfrac{{4}}{\,{11}\,}}$$$$\left.\vphantom{\dfrac{{4}}{\,{11}\,}}\right)$$ = - 1.

所以不管用哪種看法只要善用 Legendre symbol 且正確地使用 quadratic reciprocity law (記得只有奇質數才能置於 Legendre symbol 的下方), 便能快速且正確的求出 Legendre symbol 之值.