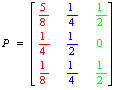數學美拾趣
許志農
我的高中同學寄給我一封電子郵件，信裡講了一則微軟總裁比爾•蓋茲的有趣故事。蓋茲是一位脾氣大，很有錢，捐錢慷慨，又很忙碌的人，他的行程都是一年前敲定的，而且敲定了就不准改變。大陸是個很大的市場，蓋茲一直想訪問大陸，見見大陸的總書記，於是透過中國的微軟負責人安排，就安排在隔年的二月五日。時間近了，微軟負責人才發現那天是大年初三，心想不妙，過年期間應該見不到總書記，於是通知蓋茲的秘書更改行程。蓋茲很不高興，在北京的首都機場責斥中國的微軟負責人：「我的行程都是一年前就排定的，而且不可以更改，這次算是破例」，而中國的微軟負責人幽默的回答「中國的新年是五千年前就排定的，也沒辦法更改。」蓋茲只好莫可奈何的苦笑。今天的主題，數學，是盤古開天以來就存在了，說起來有點奇怪，我們從小學一直到大學，我們卻都一直在學這早已存在的數學。更奇怪的是「大部分的學生都沒學好數學，而且很難欣賞數學。」《數學美拾趣》就是嘗試帶領大家來欣賞各位所學過的數學之美。
既然是欣賞數學之美，那麼態度是很重要的。在這裡引用朱光潛《談美》這本書的一小段故事，書裡談到商人､學者及畫家三種人用三種不同的態度去欣賞同一棵古松，商人想的是這棵古松的木材價值，它可以賣都少錢；學者想的是這棵古松是否為新品種，前人沒有發現過的科別；而畫家什麼事都不管，只是拿畫筆忠實的把古松畫下來。很清楚的，商人跟學者對古松的態度是有所為而為的，商人想求利，而學者為了爭名；但是畫家對古松的態度卻是無所為而為，就是欣賞古松的美而已。希望各位欣賞數學的態度能跟畫家一樣，無所為而為，就是只為了欣賞。
|
|
1.
許教授與阿基米德的胃痛拼圖合影
數缺形時少直覺，
形少數時難入微。
在加州史丹福大學同步輻射實驗室，古文物復原專家運用紫外光與數位圖像電腦處理技術，讓阿基米德發明的一道遊戲重現天日。1998年10月30日，《紐約時報》頭版登了一則報導：紐約佳士得拍賣會上，有一本其貌不揚的古書，以美金200萬的高價成交。從外表看，這本書就像是中世紀某位修士的祈禱書，磨損不堪，布滿燒焦、水漬、發霉的痕跡。然而在祈禱文的下方，隱約可看見幾乎被擦拭掉的、傳抄自古代科學家阿基米德的抄本。這祈禱書是教士約翰•麥隆納斯於公元1229年4月14日抄寫，想在耶穌復活周年日，當作禮物獻給教會。羊皮紙從古代中世紀開始使用，由於價值極為貴重，通常經過皮面刮削後，重新書寫，被稱為再生羊皮紙，麥隆納斯將祈禱文書寫在再生羊皮紙上。
透過高科技的掃瞄，祈禱書最後一頁原本是阿基米德稱為《胃痛》的一篇文章。該文章並非談身體的疼痛，而是在論述一道組合學的問題，而且附了一個正方形的插圖。
這拼圖一說是阿基米德發明的，也有人認為更早之前就被發明，阿基米德只是研究過它而已。現在只有兩條線索知道這拼圖，其一是從阿拉伯文中發現這個拼圖，在這個方向上，大都把它看成類似中國的七巧版，當成一種益智遊戲，隨意的拼出各種造型的東西；另一條線索是從一本再生羊皮書所讀出的阿基米德手稿，在這手稿中，可以確定的是：阿基米德把胃痛拼圖當成一道組合問題研究。
有幾組不同的組合學家都確認出，一共有
17152
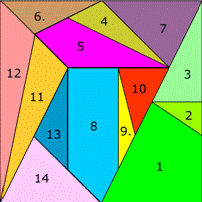
種拼法。為了美觀及容易辨識起見，我們可以將這十四塊拼圖塗上不同的顏色，右圖就是眾多不同拼法中的一種，也是很困難的一種。
阿基米德的胃痛拼圖會有這樣多的不同拼法，應該不是運氣好發現的，而是精心設計得到的，唯有將幾何與代數融合在一起，才能發明如此巧妙而多變的拼圖。接下來讓我們來談論另一件幾何與代數交融的傑作。
一百多年前（西元1899年）皮克發現並證明了三角形面積的一個有趣公式：
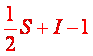
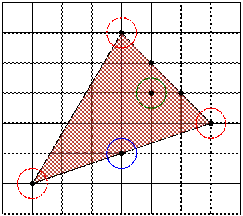
這個公式是當三角形的三個頂點都落在格子點上時才成力的，而且符號S代表落在三角形邊上的格子點數，符號 I 代表落在三角形內部的格子點數。舉例來說，下圖中的三角形邊上一共有 6 個格子點，內部有 10 格子 點，即
據皮克公式，三角形的面積為
〈皮克公式之我譯〉
每個數學公式發現之前總是有他的雛形或基本想法，究竟皮克是透過怎樣的創意發現了面積公式，我們不得而知，但是，將上圖想成鋪地磚的想法，似乎可以給我們皮克公式之合理性的一點啟發。
習題：
1. 一位年輕的老師從教書的第一天起就玩起胃痛拼圖，每天到學校的第一件事情就是拼出一幅沒拼過的胃痛拼圖。請幫這位年輕老師算一算，當這位老師退休時，是否所有的胃痛拼圖都會拼出來。
2. 在還沒有發明紙張的年代（即蔡倫之前），西方的數學知識是書寫在泥版、紙草書或羊皮紙（如巴比倫泥版、埃及紙草書、歐幾里得的幾何原本紙草書和阿基米德的再生羊皮書）上流傳，中國的數學知識利用竹簡來傳播。試論述兩者會產生怎樣的影響？
3. 將皮克公式推廣到四邊形或者多邊形，公式會有所不同嗎？試試看！
4. 在〈皮克公式之我譯〉中，說明三個頂點上的正方形磁磚與三角形相交三塊區域的面積總和為何剛好是一個正方形面積的一半？
5. 下圖左圖是最近被發現的阿基米德的《胃痛》拼圖，將正方形分個成14塊多邊形：
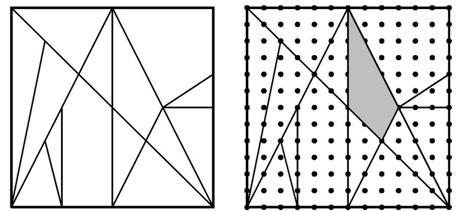
專家研究後發現，可以在邊長12公分的正方形上，正確的畫出這14塊
拼圖，如右圖所示。問：灰色那塊的面積多少平方公分。
2. 布袋和尚的播秧詩
布袋和尚的〈播秧詩〉：
手把青秧插滿田，
低頭便見水中天，
心地清淨方為道，
退步原來是向前。
唐朝布袋和尚觀察農夫播秧的情景，寫出這首有名的〈播秧詩〉，其中的「退步原來是向前」是最常被引用的句子，而「低頭便見水中天」說的卻是數學（物理）裡的鏡射原理。
不只是農夫播秧含有退步原來是向前的概念，法官讓殺人犯俯首認罪的方法也經常用到退步原來是向前的概念。想想看，法官如果一直說「你就是殺人犯」，嫌疑犯一定回應「大人啊！冤枉，我沒有殺人」，這樣下去不可能定罪。一般法官會先退一步說：「如果你不是殺人犯，那麼那天晚上你在哪裡呢？」嫌疑犯總是會說謊，然後謊越扯越大，最後就出現矛盾。暫時承認嫌疑犯沒殺人雖是退步的假設，但是矛盾的出現卻是讓案情向前的動力。
在數學的學習上，也有退步原來是向前的概念，例如：在「
不是有理數」的證明中，老師的第一行論證就是
假設
是有理數，即
…
這看起來跟法官假設嫌疑犯沒有殺人有異曲同功之妙。事實上，反證法就是「退步原來是向前」的概念運用。
習題：
1. 想想看，日常生活中還有哪些事物的運作模式可以用「退步原來是向前」來描述。
2. 懷特海是英國數理邏輯學家，曾執教於劍橋大學與牛津大學。下面是他給他的學生出的一道題目：
甲､乙､丙三人各有硬幣若干枚。甲將自己的部份硬幣分給乙､丙，使他們的硬幣各增長了一倍；之後，乙將自己的部份硬幣分給甲､丙，使他們的硬幣各增長了一倍；最後，丙將自己的部份硬幣分給甲､乙，使他們的硬幣各增長了一倍。經過這樣三次的重新分配之後，三人的硬幣都是8枚。請問甲､乙､丙三人原有硬幣幾枚。
3. 人性與推理的對話
有兩頂 2 號的帽子，三頂 3 號的帽子，將其中的三頂帽子分別戴在三人的頭上，並將其餘兩頂帽子收藏起來：
在每人只能看到另兩人頭上所戴帽子的號碼之情形下，推理自己頭上所戴帽子的號碼。
蒙提•霍爾問題是電視上的一道與博弈有關的遊戲，這個遊戲的玩法是：
參賽者會看見三扇關閉了的門，其中一扇的後面有一輛汽車，選中後面有車的那扇門就可以贏得該汽車，而另外兩扇門後面則各藏有一隻山羊。當參賽者選定了一扇門，但未去開啟它的時候，節目主持人會開啟剩下兩扇門的其中一扇，露出其中一隻山羊。然後主持人會問參賽者要不要換另一扇仍然關上的門。問題是：參賽者換另一扇門是否會增加贏得汽車的機率呢？
如果嚴格按照上述的條件的話，那麼換門是會增加參賽者贏得汽車的機率，而且贏得汽車的機會率是
。雖然該問題的答案在邏輯上並不自相矛盾，但十分違反直覺。
蒙提•霍爾問題是一道考驗人性的問題，這類問題其實只牽涉到簡易推理，沒那麼困難，但是把人性考慮進去就變得特別難。這裡所圖示的戴帽子遊戲也有同樣的道理：
習題：
1. (1) 翻閱高中數學課本或上網搜尋，說明何謂「樹狀圖」？
(2) 在 1 號門有車，2，3號門有羊的情行形下：
利用樹狀圖圖示蒙提•霍爾問題的所有情形。
2. 這是一道台積電公司招考員工的智力測驗題：
一夫，二郎，三吉，四祥，五平五個人，是青梅竹馬好朋友，如今長大成人，
各自當上麵包店老闆，理髮師，肉店老闆，菸酒經銷商和公司職員。（上面的名字和職業是任意安排的，所以不能跟名字互相對照！）
提示：
1. 麵包店老闆不是三吉，也不是四祥。
2. 菸酒經銷商不是四祥也不是一夫。
3. 此外，三吉和五平住在同一棟公寓，隔壁是公司職員的家。
4. 三吉娶理髮師的女兒時，二郎是他們的媒人。
5. 一夫和三吉有空時，就和肉店老闆，麵包店老闆打牌。
6. 而且，每隔十天，四祥和五平一定要到理髮店修個臉。
7. 但是，公司職員則一向自己刮鬍子，從來不到理髮店去。
問題：請將這五個人的名字和職業連接起來！
|
一夫 二郎 三吉 四祥 五平 |
麵包店老闆 理髮師 肉店老闆 菸酒經銷商 公司職員 |
4. 超完美的人體實驗
我們經常用「頭腦簡單，四肢發達」來調侃運動員，但是美國跳高選手福斯貝里的背越式跳高卻是跳高革命的先行者。他讓自己的身體在拋物線上挑戰高度，締造了完美的人體實驗。
石頭或球一離手，它們的運動軌跡，即拋物線，就已經完全決定了，這是大家共有的經驗，也是物理學的基本定律。將這項鐵律運用在跳高上，可就精彩多了，問題就出在人的身體可以作超完美的旋轉與伸屈。
在過去的歷史中，人們發展出跨越式､剪式､滾式､俯臥式及背越式這五種跳躍過竿的動作：
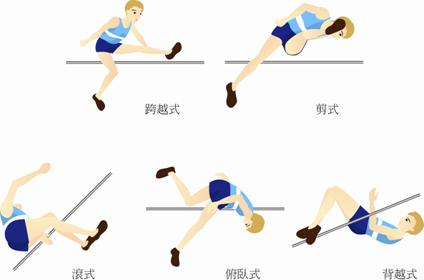
跳高選手一旦離開地面處於無支橕狀態，身體重心的運動軌跡將不可改變，身體重心所滑出的拋物線就會被完全確定下來，但是身體重心只是人體平衡重量的一個點，隨著身體不同的伸縮，可以讓重心處於身體的上方，內部或者下方，而背越式就是讓重心處於身體下方的一種跳高方式。背越式的革命性意義在於運動員的身體形成『反弓』和『背橋』，頭、肩、背、腰、臀、腿部『分期分批，化整為零』依次滑過橫杆，完全不同於其他跳高形式中身體必須在瞬間『一攬子』過杆。
談到超完美的人體實驗就讓我想起一則有膽識的人體實驗之故事，美國一位有名的物理學家在課堂上以自己的頭當賭注，挑戰鐘擺原理。教授拿一條粗繩綁住一顆鉛球掛在屋頂上，教授站在垂繩不遠處並手拿鉛球，讓鉛球與頭接觸。此時教授將手上的鉛球放開，鉛球繫在繩上會做來回的鐘擺運動。當繩子將鉛球擺回時，學生一定會擔心鉛球是否會在教授的面前停下來。如果你相信力學原理，教授一定會毫髮無傷。教授就是藉著這實驗讓學生深刻體會鐘擺的力學。
習題：
1. 1. 有一面一公尺高的圍牆，分別讓一顆球，一支筆，一條狗及一個人越過此圍牆。試就四種物體的重心所產生之拋物線來討論四者越過圍牆的差異程度。
2. 2. 標槍比賽中，選手投擲出標槍。試描述標槍重心在空中所畫出的拋物線軌道與標槍的關係。
5. 倫琴夫人的手掌透視照片
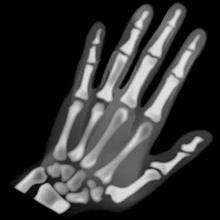
倫琴1895年宣布X光的存在，並發表了他那張著名的手掌透視照片，讓我們清楚手部骨骼構造與瞭解各塊骨頭長度的比例。
倫琴為了幫受傷的太太瞭解手掌受傷的程度，用他所發明的X光機幫其夫人照了一張有名的手掌透視照片。從片中清楚看出，大拇指自指尖到腕骨是由三塊骨頭所構成（第三塊在手掌旁邊），而其餘四指都是由四塊骨頭所連接而成（第四塊在手掌內部裡）。
以中指四塊骨頭長度（自中指尖到腕骨）來說明，令其從短到長的長度
依序為
,
也就是說，中指四塊骨頭中，最短的那一節之長度為 a，第二節的長度為b，第三節長度是 c，藏在手掌那節的長度為d 。根據統計，當這四節成等比數列，而且公比為
時，中指看起來最完美。
同時，手掌的每隻手指頭的每節長度都呈現公比為
的等比數列時，手掌看起來最漂亮。
習題：
1. 拿尺量一量你的大拇指三塊骨頭的長度，並令從短到長的長度依序為
a, b, c.
選出符合的條件：
(1) a, b, c 約略成等差數列。
(2) a, b, c 約略成等比數列。
(3)
a,
b,
c 大約滿足
。
2. 設完美大拇指三節長度分別為 a, b, c ，證明
.
3.
當你數到
時，會數在哪根手指頭上？
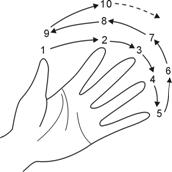
6. 舉手投足都是美
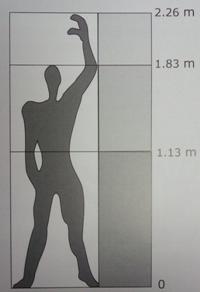
羅伯特•文森特整理一本很有趣的美學書籍，它的書名叫做《黃金比例的幾何》，在這本書裡，文森特搜集了相當豐富的各種幾何圖片，而這些圖片所呈現的共通點就是都跟黃金比例有關，黃金比例 1.618 是書裡所要傳達的唯一數字。
左圖就是書裡的一幅人體幾何圖，描述人們舉手投足的美學比例，而右側所標示的高度正是人體美學的密碼，究竟高度 1.13, 1.83 與 2.26 與黃金比例 1.618 產生怎樣的共鳴呢？
達文西是將人體各部位的比例研究得相當清楚的科學家，關於人體比例，肚臍扮演著舉足輕重的角色。在圖中，一個人將手舉高，頭頂到手指最高點的距離為 a，頭頂到肚臍的距離為b，肚臍到腳底的距離為 c 。人體美學告訴我們，當這三數 a, b, c 成等比數列，而且公比為
時，身體比例最理想。
1. 右圖是手上高舉一顆球的素描圖，從上而下四條平行線之間的距離分別為 a, b, c。當此人身體比例最理想時，證明
。
2. 洗澡時拿皮尺量一下自己的肚臍高度及身高，並算一下
這個比值。
3. 承上題，如果身體比例最理想，那麼
這個比例應該是多少。
4. 志玲姊姊身高173公分，肚臍高度105公分。請問志玲應該穿幾公分（取整數）高的高跟鞋，才會看起來最像完美女人？
7.
阿基米德的馱龜幻想曲
割之彌細，所失彌少，
割之又割，以至於不可割，
則與圓周合體而無所失矣。
劉徽為了論述圓面積發明了割圓術，並將割圓術的精神用文字「割之彌細，所失彌少，割之又割，以至於不可割，則與圓周合體而無所失矣」來描述。不僅是東方的劉徽對圓有“割之又割，以至於不可割”的困擾，西方的阿基米德在求拋物線的弓形面積時，也發生同樣的情況。他們所不同的是，阿基米德採取了馱龜的比喻來闡釋拋物線的弓形面積。就讓我們來欣賞阿基米德的馱龜幻想曲：
一隻大烏龜馱上兩隻中烏龜，這兩隻中烏龜的重量都是大烏龜的八分之ㄧ，又每隻中烏龜又背著兩隻小烏龜，這兩隻小烏龜的重量也都是中烏龜的八分之ㄧ，如此疊上去。
已知最底下的大烏龜有3公斤重，求所有烏龜的總重量？
拋物線與弦所圍的區域稱為拋物線的弓形，世界上第一位會算拋物線弓形面積的人是兩千多年前的阿基米德。阿基米德以弦為底畫出一個三角形，之後在兩邊再各畫一個三角形，如下圖所示：
阿基米德說：「如果依照這樣的規律一直畫下去，那麼這些三角形的面積總和就會是拋物線的弓形面積。」直觀看來，兩者的差異愈來愈小，問題是，這些三角形有無窮多個，而且不知道其面積總和該如何求？阿基米德進一步說：「馱在上面的兩個三角形之面積和是底下這個三角形面積的四分之一，由此可推得拋物線的弓形面積是最大三角形面積的三分之四倍。」在沒有微積分的幫忙之下，能夠算出這樣的結果，算是出類拔萃之人。
將上述情境中的三角形改成烏龜，面積視為烏龜的重量，就是這裡所談的問題！
“割之又割，以至於不可割”與“畫之再畫，以至於不可再畫三角形”是劉徽與阿基米德所碰到的共同困擾。物理學家費曼先生提過一則有趣的故事：「給你一顆橘子及一把刀，將橘子切成薄片，有辦法讓薄片薄到足以蓋著整個地球表面嗎？」費曼利用這道問題來檢驗學生是數學思考還是物理考量。
習題：
1. 利用無窮等比級數的求和公式算烏龜的重量總和。
2.
請討論費曼先生的問題。
3. 右圖是半徑為 1 的圓與邊長為 2 的正方形相切的情形：讓電腦隨意從正方形內選出 1000 個點，你認為這1000 個點中有幾個點會落在圓內。
8.
生鏽圓規大搞數學工藝
尼采有一段耐人咀嚼的哲學思考：「當你見到猿猴笨拙的行為時，你該覺得好笑還是自卑呢？到底是取笑猿猴的不靈活，笨手笨腳的行為，還是對笨拙的猿猴可以演化出人類，而我們似乎很難比牠們進步得更多感到自卑呢？」
下圖是在平面上，給定兩個已知點 A 及 B，只利用一把生鏽的圓規作出 C 點，讓 ABC 為正三角形的作圖過程：
9. 條條道路通蟻窩
患痴呆的老人容易迷路，回不了家，原因出在他們是靠記憶，而非靠幾何記得家的位置。你也是靠死記回家的嗎？
螞蟻可不是這樣回家的，牠們有一套回家的幾何學！
螞蟻只能看到平面（二維空間）的事物，只能在二維空間內做
方向上的任意運動。雖然螞蟻只生活在平面上，但是科學家卻發現螞蟻天生具有某種幾何的洞悟力，能利用幾何原則尋找回窩的路。螞蟻的路線系統就像羅馬人的道路一樣…條條道路通羅馬；對螞蟻來說…條條路線通蟻窩。
要了解螞蟻尋找方向的訣竅，可以假想有一個「Y」字母的交叉點，而一隻離開蟻窩的螞蟻從「Y」字母底下往上爬，碰到這樣一個叉路，發現有兩條以狹窄角度交叉的路線。相反地，回窩的螞蟻會碰到兩條叉路：一條的交叉角度較小，而另一條的角度大得多，角度較大的那一條路才是回家的路。也就是說，螞蟻的網路是由「Y」字來構成，而且較小的交叉角是
左右，科學家稱它為「六十度法則」。如圖所示，一隻螞蟻從蟻窩出來，朝東邊方向以六十度法則向外覓食，而這蟻窩裡的螞蟻構造了向東及向西兩個方向的覓食網。
習題：
1. 右圖中的螞蟻從西邊走出蟻窩：若每次碰到「Y」字母的交叉點時，螞蟻都選擇左邊的叉路離去，則這隻螞蟻最後會遠離蟻窩，還是回 到蟻窩呢？
2. 右圖是十個圓圈點所畫出的網路，試著描述你的發現，如路徑有幾種顏色構成，任意兩圓圈都可以經過至多幾段路徑就能連接，想成立體圖，十個圓圈是一樣的嗎？提出越多有趣的性質越好。
10.
三國華容道
在赤壁之戰中：
關羽於華容道放走曹操，數學家以
關羽橫讓捉放曹操
為標題將故事寫成益智遊戲。
華容道、孔明棋和魔術方塊被喻為世界三大不可思議的益智遊戲，其中華容道是一道滑板遊戲，出自三國演義中「關羽橫讓捉放曹操」的情節。事實上，華容道是中國古代的一個地名，相傳當年曹操在赤壁之戰後曾經敗走此地。由於當時的華容道是一片沼澤 ，所以曹操大軍要割草填地，不少士兵更慘被活埋，慘烈非常。
華容道棋盤為橫四格縱五格的盤面，曹操是占四格的正方形棋子；占兩格的有五虎將的關羽､張飛､趙雲､馬超與黃忠，其中只有關羽是橫兩格，其餘四將均為豎兩格；還有四個各占一格的兵。在遊戲時，只能利用盤面上留下的兩個空格來移動棋子，只要想辦法將曹操移到鄰接曹營上方的正中央的位置，即表示我們已成功讓曹操逃回曹營，遊戲至此於是結束。
11.
數列魅影
等差數列與等比數列是每位學生都懂得數學知識：
猜猜看那個圖形的藍綠紅區域面積是等差數列？又何者是等比數列？
在綠､藍､紅四邊形區域的圖形中，上方的三條線段等長，而下方的三條線段等長亦等長，一個美妙的幾何性質是說：「綠､藍､紅四邊形區域面積構成等差數列。」這是教育部九十七學年度高級中學數學科能力競賽決賽的口試試題。當中有一位學生提出妙解，解法如下：
作如下的補助線，利用同底等高可以得到圖中面積分別為 
的四個三角形：
同樣利用同底等高可以得到
將兩式相加，得
即
證得四邊形
的面積構成等差數列。
■
不僅等差數列有好的幾何圖形示例，等比數列也有，下圖中的綠､藍､紅三圓之面積構成等比數列。
習題：
證明：綠､藍､紅三圓之面積構成等比數列。
12.
眼球定理
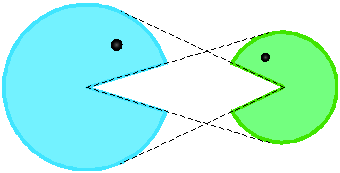
學幾何的人都喜歡將所學的幾何定理用生活中的事物來比喻，這裡所要介紹的「眼球定理」就是一個實例。
不過個人比較想要把眼球定理想成大小精靈互吃對方的定理，想想看，大小精靈互相看對方不順眼時，都張大他們的嘴巴，想把對方一口給吃掉，這個圖形可以啟發或引起怎樣的幾何定理呢？
如下圖所示，圓
與
是兩個相離的圓，從圓心
向圓
引公切線，這兩條公切線會與圓
交於兩點，令這兩點的距離為
；同樣地，從圓心
向圓
引公切線，這兩條公切線會與圓
交於兩點，令這兩點的距離為
：
眼球定理告訴我們：
，也就是說，大小精靈體積不同，但他們所張開的嘴巴是一樣大的。
習題：
1. 「蝴蝶定理」是幾何學裡一個漂亮的定理，由於其幾何圖形貌似蝴蝶，便以此命名。請上網輸入「蝴蝶定理」查詢，並依據下圖寫出這個定理的正確敘述，且指出蝴蝶意指圖中的哪一個形狀：
2. 利用以下所提示的提示及輔助圖形證明眼球定理：
提示：利用兩圓半徑
與
及直角三角形的比例寫出兩個
的
值，並得到
的公式，同樣的方法，得到
的公式。最後比較兩公式。
3. 將下列幾何定理連連看：
|
l 畢氏定理 |
u
|
|
l 餘弦定理 |
u
|
|
l 正弦定理 |
u
|
|
l 平行四邊形定理 |
u
|
|
l 海龍公式 |
u
|
13.
地球平面圖
橘子的皮可以剝掉，但無法讓這些皮躺平在平面上，同理，用地圖來表示地球表面的相關位置也會碰到難題。幾何學家如何處理這樣的難題呢？
經線與緯線是地球上最重要的兩組線，它們是互相垂直的兩組大圓線，而赤道又是最重要的一條緯線。如同橘子皮無法攤平在桌面上一樣，想將地球表面繪製成一張平面式的地圖也是沒辦的。右圖是一種投影式的製圖方式，想像將一張紙張圍成圓柱，且剛好與地球的赤道相切。此時，從地球中心將地表投影在該紙張上，就形成地圖。這樣製成的地圖有幾項特色：
(1) 南極與北極不在地圖上，這是因為它們兩點被投影至無窮遠處的關係。
(2) 南北兩極附近的土地變形，而且變大了，這是因為讓紙張與赤道相切的關係。
(3) 緯線被投影成水平線，而經線變成鉛直線。
這裡所介紹的地圖稱為麥卡托圓柱投影法繪成的地圖。
習題:
1. 用麥卡托圓柱投影法繪成的地圖，圖上不一定成直線的是
（A）經線 （B）緯線（C）同方位線（D）大圓線 （E）赤道。
2. 世界第一大島格陵蘭的面積約為南美洲的九分之一，但在麥卡托圓柱投影法繪成的地圖上來看，面積幾乎一樣。究竟問題出在哪裡？
3. 地球上想同距離的兩點，投影在地圖上是否都等距。
4. 上網查詢，寫出兩種繪製地圖的其他方法。
5. 我們在兔子的身體表面上制作圖形，下圖是2006年刊登在紐約時報，在兔子的身體上我們有互相垂直的曲線，攤平在平面上就是普通的坐標系統。這是丘成桐院士在〈古典幾何在電腦繪圖及醫學影像之應用〉演講中的舉例：
說明你對這兩個表面圖形的觀察與領悟。
14. 柯施克的正十二邊形定理…典雅的鑲嵌
同樣邊長的正三角形､正方形與正十二邊形磁磚可以鑲嵌､鋪滿整個平面。正十二邊形究竟有何魅力？且讓我們來欣賞匈牙利數學家柯施克利用幾何鑲嵌所證明的一道定理：
半徑
的圓內接正十二邊形的面積剛好為
。
以數學為內容的競賽有著悠久的歷史：古希臘時就有解幾何難題的比賽；十三世紀在義大利有所謂的宮廷數學競賽，斐波那契參加過這項考試，其著作《花朵》就涵蓋了宮廷數學競賽的一些問題；十六世紀在義大利有過關於塔塔利亞求解三次方程的激烈競爭；十七世紀，不少數學家喜歡提出一些問題向其他數學家挑戰，費馬所提出的費馬大定理就是一個例子；十九世紀，法國科學院以懸賞的方法徵求對數學難題的解答，常常獲得一些重要的數學發現，高斯就是比賽的優勝者。但是，專門以中學生為對象的數學競賽源於匈牙利，在 1894 年，匈牙利舉辦第一屆由高中學生參加的數學競賽，此競賽每年十月舉行，每次出三題，限四小時完成，允許使用任何參考書。到今天已經舉辦了一百多屆，為了感謝匈牙利數學家柯施克（J. Kurschak, 1864∼1933）當初對此競賽所付出的努力及其對數學的貢獻，這項比賽也改以柯施克數學競賽來命名。我們在市面買到的匈牙利數學競賽問題與解答就是當年柯施克編輯的。
在中學幾何，柯施克有一項重要成就，他不用面積的代數公式，而單純只用幾何構造，證明了「單位圓內接正十二邊形的面積剛好為
。」
上圖就是柯施克構造正十二邊形的方法：
(1) 先畫一個大正方形，分別將此正方形的四邊向內畫出四個正三角形。
(2) 這四個正三角形的頂點（在大正方形內）構成一個小正方形。
(3) 將小正方形四邊上的四個中點與四個正三角形的八個交點（如上圖所
示）依序連接起來，構成一個十二邊形。
根據柯施克構造法所畫出的十二邊形為正十二邊形，甚至柯施克還將小正方形進一步分割，讓這小正方形被分割成正三角形
與鈍角等腰三角形
，如下圖所示：
柯施克用正三角形與鈍角等腰三角形來鑲嵌正方形，其中用了
個正三角形與
個等腰三角形。如果小正方形的邊長為
，即柯施克構造的十二邊形為單位圓內接正十二邊形，那麼小正方形的面積與個正三角形與個等腰三角形的面積和一樣，即
又柯施克正十二邊形是由
個正三角形與
個等腰三角形鑲嵌而成，因此其面積為
這就是柯施克定理的推理過程，既神奇又漂亮吧！
習題:
1. 求正十二邊形的一個內角度數。
2.
當柯施克小正方形的邊長為時（即柯施克正十二邊形為單位圓內接正十二邊形），求外面的大正方形邊長。
3.
利用高中所學的面積公式證明：單位圓內接正十二邊形的面積為。
4.
求鈍角等腰三角形的最大內角度數。
5.
下圖是將單位圓內接正十二邊形分割成正三角形，正方形與正六邊形的情形。若
分別代表正三角形與正方形的面積，則利用柯施克定理求下列的值：
(1)
(2)
.
15. 轉移矩陣
