Index


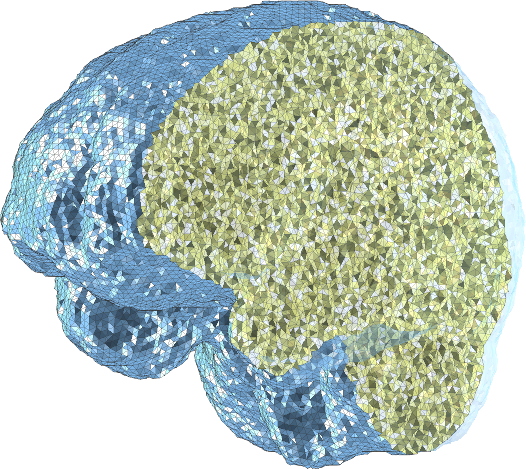
Volume-Preserving Parameterizations of Simplicial 3-Manifolds

The issue aims to find a volume-preserving mapping that maps a simplicial 3-manifold to a specified canonical domain.

           


Related Publications

  1. Convergence Analysis of Volumetric Stretch Energy Minimization and its Associated Optimal Mass Transport
    (with T.-M. Huang, W.-H. Liao, W.-W. Lin and S.-T. Yau)
    SIAM Journal on Imaging Sciences, 16(3):1825–1855, 2023.
    [Publisher's Version] [Full Text]

  2. Projected Gradient Method Combined with Homotopy Techniques for Volume-Measure-Preserving Optimal Mass Transportation Problems (with T.-M. Huang, T. Li, W.-W. Lin and S.-T. Yau)
    Journal of Scientific Computing, 88(3), 2021.
    [Publisher's Version] [Full Text]

  3. A New Efficient Algorithm for Volume-Preserving Parameterizations of Genus-One 3-Manifolds (with T. Li, W.-W. Lin and S.-T. Yau)
    SIAM Journal on Imaging Sciences, 13(3):1536–1564, 2020.
    [Publisher's Version] [MathSciDoc] [Project Page]

  4. A Novel Algorithm for Volume-Preserving Parameterizations of 3-Manifolds (with T. Li, W.-W. Lin and S.-T. Yau)
    SIAM Journal on Imaging Sciences, 12(2):1071–1098, 2019.
    [Publisher's Version] [Full Text] [MathSciDoc]

Area-Preserving Parameterizations of Simplicial Surfaces

The issue aims to find a area-preserving mapping that maps a simplicial surface to a specified canonical domain.

       

Related Publications

  1. Convergent Authalic Energy Minimization for Disk Area-Preserving Parameterizations (with S.-Y. Liu)
    Journal of Scientific Computing, 100(2):43, 2024.
    [Publisher's Version] [Full Text] [Preprint] [BibTex]

  2. Riemannian gradient descent for spherical area-preserving mappings (with M. Sutti)
    AIMS Mathematics, 9(7):19414–19445, 2024.
    [Publisher's Version] [Preprint] [BibTex]

  3. Theoretical Foundation of the Stretch Energy Minimization for Area-Preserving Simplicial Mappings
    SIAM Journal on Imaging Sciences, 16(3):1142–1176, 2023.
    [Publisher's Version] [Full Text] [BibTex]

  4. A Novel Stretch Energy Minimization Algorithm for Equiareal Parameterizations (with W.-W. Lin, C.-T. Wu and S.-T. Yau)
    Journal of Scientific Computing, 78(3): 1353–1386, 2019.
    [Publisher's Version] [Full Text] [MathSciDoc] [MATLAB Demo]

Conformal Parameterizations of Simplicial Surfaces

The issue aims to find a conformal mapping that maps a simplicial surface to a specified canonical domain.

           

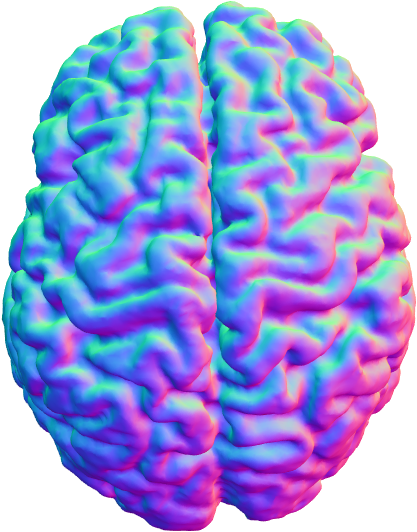
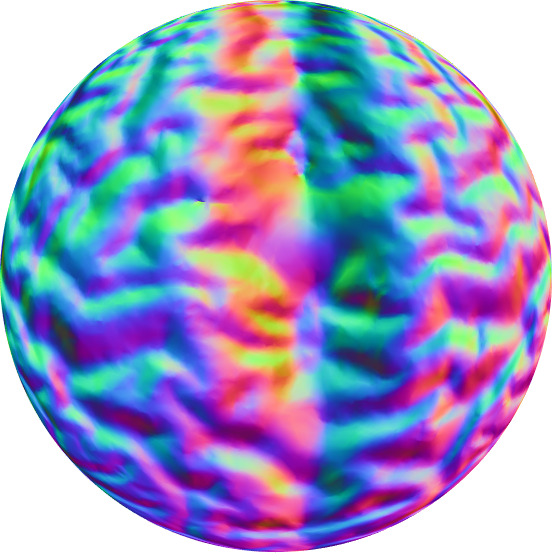
Related Publications

  1. Convergence Analysis of Dirichlet Energy Minimization for Spherical Conformal Parameterizations
    (with W.-H. Liao, T.-M. Huang and W.-W. Lin)
    Journal of Scientific Computing, 98:29, 2024.
    [Publisher's Version] [Full Text] [Preprint]

  2. A Constructive Algorithm for Disk Conformal Parameterizations (with W.-H. Liao)
    Journal of Scientific Computing, 92(2), 2022.
    [Publisher's Version] [Full Text] [Project Page]

  3. Convergent Conformal Energy Minimization for the Computation of Disk Parameterizations (with Y.-C. Kuo, W.-W. Lin and S.-T. Yau)
    SIAM Journal on Imaging Sciences, 14(4):1790–1815, 2021.
    [Publisher's Version] [MathSciDoc] [Project Page]

  4. An Efficient Energy Minimization for Conformal Parameterizations (with W.-W. Lin, C.-T. Wu and S.-T. Yau)
    Journal of Scientific Computing, 73(1): 203–227, 2017.
    [Publisher's Version] [Full Text] [Preprint] [MATLAB Demo]

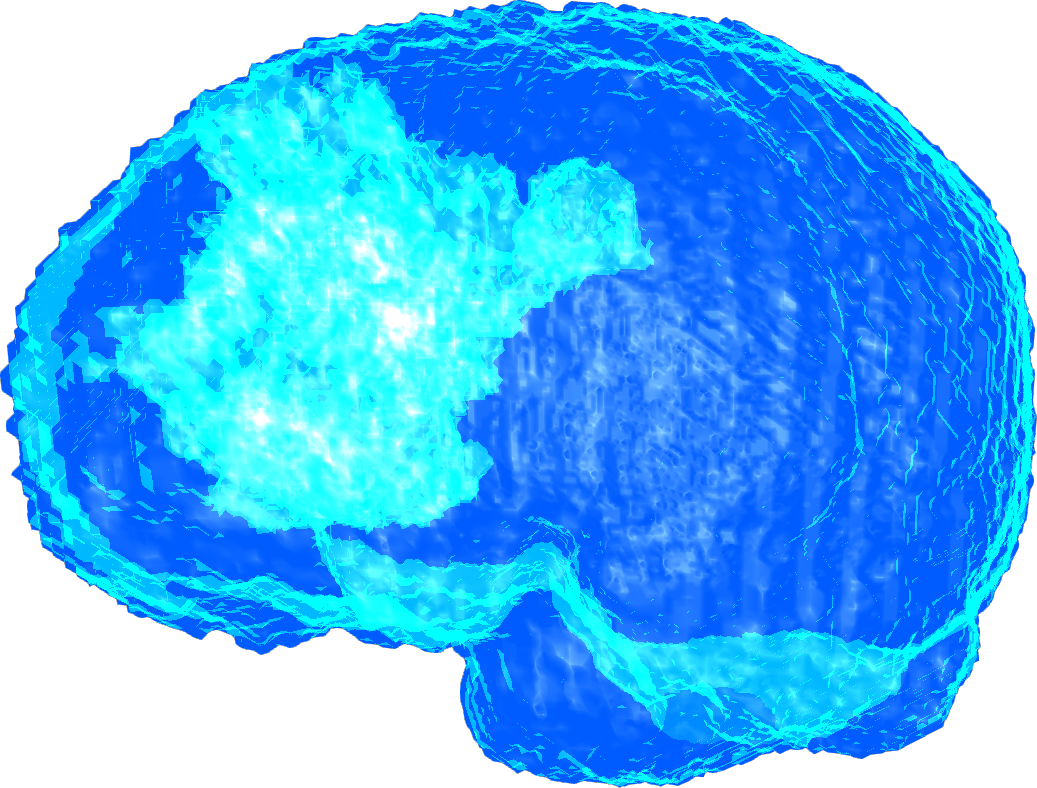
Brain Tumor Segmentation

This issue aims to automatically segment pixels of tumor regions in an image tensor obtained from CT or MRI.

       

Related Publications

  1. A Two-Phase Optimal Mass Transportation Technique for 3D Brain Tumor Detection and Segmentation
    (with W.-W. Lin, T. Li, T.-M. Huang, J.-W. Lin and S.-T. Yau)
    Lecture Notes in Computer Science, vol 12962. Springer, Cham., 2022.
    [Publisher's Version]

  2. A novel 2-phase residual U-net algorithm combined with optimal mass transportation for 3D brain tumor detection and segmentation
    (with W.-W. Lin, J.-W. Lin, T.-M. Huang, T. Li and S.-T. Yau)
    Scientific Reports, 12, 6452, 2022.
    [Publisher's Version] [Full Text]

  3. 3D Brain Tumor Segmentation Using a Two-Stage Optimal Mass Transport Algorithm
    (with W.-W. Lin, C. Juang, T.-M. Huang, T. Li, S. Wang and S.-T. Yau)
    Scientific Reports, 11, 14686, 2021.
    [Publisher's Version] [Full Text]

Applications of Simplicial Surface Parameterizations

  • Brain Tumor Visualization

    The video shows a tumor in the human brain and its volume-preserving parameterization on a unit ball.



  • Brain Deformation

    The deformation of the human brain is subtle and not easy to be observed. The one-to-one correspondence between two brain surfaces is necessary to detect the deformation efficiently. With the efficient parameterization algorithms for genus zero closed surfaces, the registration problem between two brains is reduced to the registration problem on the unit sphere, which is much easier since the shape of the domains is identical. Then, the deformation from one brain to another can be visualized via the homotopy between the identity mapping and the registration mapping between the two brains.



  • Area-Preserving Intestine Flattening

    Polyps are the predecessor of intestinal cancers. However, polyp detection is usually not easy, especially when the polyps are hidden in the folds. To efficiently detect the polyps on the intestinal surface, an area-preserving mapping can be applied to flatten the surface to a rectangle domain so that the polyps can be easily found in the rectangle domain. Then the exact locations of polyps can be obtained by the one-to-one correspondence between the intestinal surface and the rectangle domain.



  • Hippocampus Deformation

    It is known that the deformation of the hippocampus can detect Alzheimer's disease. The deformation can be measured via the one-to-one correspondence between two surfaces of hippocampi. Similar to the brain mappings, the mapping between two hippocampi can be obtained via the registration mapping on the spherical domain of parameterization mappings.



  • Surface Morphing

    The aim of surface morphing in 3D is to use less quantity of mesh frames to construct a smooth 3D video. The registration mappings between each pair of surfaces play a crucial role. With suitable parameterizations, the registration problems between surfaces are reduced to the registration problems on a domain of a unified shape. Then the smooth video in 3D is constructed via the cubic spline homotopy between each pair of registration mappings.



    A demo video of surface morphing between four facial expressions.

  • 3D Video Compression

    The 3D video, captured using the 3D scanner, contains 30 surfaces and texture images per second. Each surface data is of size roughly 30 megabytes. The goal of 3D video compression is to use less quantity of the raw data of a 3D video to approximate the original 3D video. Note that each frame of the 3D video is a simply connected open surface, which is conformally equivalent to a unit disk. The conformal equivalence can be computed efficiently and accurately using the proposed algorithm. Then the diffeomorphism between each pair of surfaces can be constructed on the disk. Ultimately, the video sequence is reconstructed by the cubic spline homotopy between each pair of diffeomorphisms. As a result, the whole video sequence is reconstructed by merely 1.6% of the original data while the resolution of the video is preserved.



    The original video of the chewing-gum motion (right) and the reconstructed video by the spline homotopy using 1.6% of the original data (left).

  • Texture Mapping

    Texture mapping refers to replacing the texture of a surface with another one. It has been widely applied to the movie industry, e.g., the famous movie, Avatar. In the film, actors and actresses perform without heavy makeup. Instead, a virtual makeup technique creates a lifelike visual effect. The key issue is to find an appropriate diffeomorphism between the surface and the desired texture image that preserves features. The texture image is regarded as a planar surface in 2D, so the diffeomorphism between the mesh and the texture image can be computed similarly. With the proposed algorithm, virtual makeup can be performed efficiently and robustly.



    A demo video of texture mapping.

  • Virtual Broadcasting

    Because each Chinese syllable comprises 1 to 3 Mandarin phonetic symbols, a virtual broadcasting system can be realized by recording videos of pronouncing all 37 phonetic symbols and constructing the morphing sequences.



    A demo video of automatic Chinese virtual broadcasting.

  • Motion Retargeting

    Motion retargeting aims to use the information from a sequence of 3D videos to drive a target surface. In other words, the motion of a target surface model is controlled by the movement of a given 3D video. The application already appears in iPhone X. By applying the proposed algorithm, the conformal equivalence can be efficiently computed. The feature-preserving diffeomorphism between each pair of surfaces is constructed on the disk. Next, a vector field is constructed by the difference of two consecutive frames. Then the embedding of the target surface is controlled by the vector field via the topological equivalence.



    A morphing sequence of the chewing-gum motion (left) and the motion retargeting on a target model (right).

Related Publications

  1. An optimal transportation-based recognition algorithm for 3D facial expressions (with T. Li and P.-S. Chuang)
    Annals of Mathematical Sciences and Applications, 7(1):49–96, 2022.
    [Publisher's Version]

  2. Optimized Surface Parameterizations with Application on Chinese Virtual Broadcasting (with H.-H. Huang, T. Li, W.-W. Lin and S.-T. Yau)
    Electronic Transactions on Numerical Analysis, 53:383–405, 2020.
    [Publisher's Version] [Abstract] [Full Text]

Nonlinear Signal Filtering

The nonlinear filtering issue has a variety of applications in military, engineering, and commercial industries. The issue aims to determine the conditional probability density function of the unknown state via a given observation history.

Related Publications

  1. An efficient numerical method for solving high-dimensional nonlinear filtering problems (with W.-W. Lin and S.-T. Yau)
    Communications in Information and Systems, 14(4): 243-262, 2014.
    [Publisher's Version] [Full Text] [MATLAB Demo]

  2. An efficient algorithm of Yau-Yau method for solving nonlinear filtering problems (with W.-W. Lin and S.-T. Yau)
    Communications in Information and Systems, 14(2): 111-134, 2014.
    [Publisher's Version] [Full Text] [MATLAB Demo]