証 明.
(1) 我們利用第一個 group action (
G,
S,*) 來證明
r |
m. 由式子
(
4.19) 知: 任選
P'  S
S, 我們有
r = |
G|/|
N(
P')|. 不過
Lemma
4.4.1 告訴我們
P' 是
N(
P') 的 subgroup. 由於
|
P'| =
pn, Lagrange 定理告訴我們 |
N(
P')| 是
pn 的倍數, 又由於
N(
P') 是
G 的 subgroup, 再用一次 Lagrange 定理得
|
N(
P')| =
pnd
其中
d |
m. 故知
因此
r |
m.
(2) 我們利用第二個 group action (P, S,*) 來證明
r 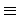 1(mod p). 因 P 是一個 p-group, 由 Proposition 4.1.4 知
1(mod p). 因 P 是一個 p-group, 由 Proposition 4.1.4 知
r = | S| 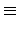 | S0|(mod p). | S0|(mod p). |
(4.22) |
我們現在來計算 |
S0|. 由式子 (
4.20) 知若
P'  S0
S0 則
P  N
N(
P'). 不過前面已知
|
N(
P')| =
pnd, 其中
d |
m.
然而由
p m
m 知
p d
d, 因此由 |
P| =
pn 知
P 是
N(
P')
的一個 Sylow
p-subgroup. 另一方面, 由 Lemma
4.4.1 知,
P'
是
N(
P') 的 normal subgroup. 但
P' 也是
N(
P') 的 Sylow
p-subgroup. Corollary
4.5.2 告訴我們
P' 是
N(
P')
唯一的 Sylow
p-subgroup. 故得
P =
P'. 換句話說
S0 中只可能有
P 這個元素. 因此由式子 (
4.21) 知
S0 = {
P}, 也就是說
S0
只有一個元素. 故由式子 (
4.22) 得
r 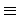
1(mod
p).

Example 4.6.2 (1)
我們知道在
A4 中 Sylow 3-subgroup 並不唯一 (Example
4.5.3), 那麼
A4 到底有多少個 Sylow 3-subgroup 呢? 假設有
r
個, 由於
|
A4| = 4
. 3, 由第三 Sylow 定理 (Theorem
4.6.1)
知
r | 4 且
r = 3
k + 1. 也就是
r = 1 或
r = 4. 由於已知
r
1,
故得
r = 4. 事實上在
A4 中由
(1 2 3), (1 2 4), (1 3 4), (2 3 4)
這四個 3-cycles 個別產生的 cyclic group 皆相異, 故知這些就是所有
A4 的 Sylow 3-subgroup.
(2) 在 A5 中有多少 Sylow 5-subgroups 呢? 假設有 r 個, 由於
| A5| = 5!/2 = 5 . 12, 由第三 Sylow 定理 (Theorem 4.6.1) 知
r | 12 且 r = 5k + 1. 也就是 r = 1 或 r = 6. 由於已知 A5 是
simple (Theorem 3.4.26) 所以 A5 的 Sylow 5-subgroup 不可能是
A5 的 normal subgroup. 因此由第二 Sylow 定理 (Corollary
4.5.2) 知 r 1. 故得 r = 6. 事實上在 A5 中所有的
5-cycle 共有 4! = 24 個 (為甚麼呢?
這是高中的排列組合中五個人坐圓桌的問題吧!). 不過任一個 5-cycle
所產生的 cyclic group 中有 4 個 5-cycle 出現.
例如:
1. 故得 r = 6. 事實上在 A5 中所有的
5-cycle 共有 4! = 24 個 (為甚麼呢?
這是高中的排列組合中五個人坐圓桌的問題吧!). 不過任一個 5-cycle
所產生的 cyclic group 中有 4 個 5-cycle 出現.
例如:
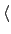
(1 2 3 4 5)
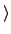
= {(1 2 3 4 5),(1 3 5 2 4),(1 4 2 5 3),(1 5 4 3 2),
I}
因此這 24 個 5 cycle 只產生 24/4 = 6 個相異的 order 5 的
subgroup. 這就是所有
A5 的 Sylow 5-subgroup.
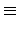 1(mod p).
1(mod p).
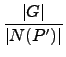 =
= ![]() 1(mod p). 因 P 是一個 p-group, 由 Proposition 4.1.4 知
1(mod p). 因 P 是一個 p-group, 由 Proposition 4.1.4 知
![]() 1. 故得 r = 6. 事實上在 A5 中所有的
5-cycle 共有 4! = 24 個 (為甚麼呢?
這是高中的排列組合中五個人坐圓桌的問題吧!). 不過任一個 5-cycle
所產生的 cyclic group 中有 4 個 5-cycle 出現.
例如:
1. 故得 r = 6. 事實上在 A5 中所有的
5-cycle 共有 4! = 24 個 (為甚麼呢?
這是高中的排列組合中五個人坐圓桌的問題吧!). 不過任一個 5-cycle
所產生的 cyclic group 中有 4 個 5-cycle 出現.
例如: