


�U�@��: �u�ʥN�ƪ�����
�W�@��: ��� Field ���ʽ�
�e�@��: Field ���ʽ�
��@�몺 field F, �Y a  F, �ѩ� 1
F, �ѩ� 1  F, �G����N��
n
F, �G����N��
n 
 �ڭ̦�
�ڭ̦�
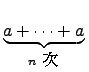 = ( = (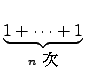 ) . a. ) . a. |
(9.1) |
�n�`�N�b�o�� 1 �[ n ���ä����� n, �o�O�ѩ�o�̪� 1 �O F
���� 1 �ä��O�۵M��
 ���� 1. �Ҧp�W�Ҥ�
���� 1. �Ҧp�W�Ҥ�
 �O
�O
 /5
/5 ���� 1, ��
�Ӧb
���� 1, ��
�Ӧb
 �� 5 �O������ 0 ��. �ҥH�ڭ̤���⦡�l (9.1) �g��
�� 5 �O������ 0 ��. �ҥH�ڭ̤���⦡�l (9.1) �g��
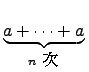
=
n . a.
���L���F��K, ����N a  F �B
n
F �B
n 
 �ڭ̥� na �Ӫ��� a
�ۤv�[�ۤv n ��, �]�N�O��
�ڭ̥� na �Ӫ��� a
�ۤv�[�ۤv n ��, �]�N�O��
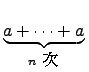
=
na.
�Ʊ椣�|�y���j�a���x�Z. �]���ڭ̥i�H�N���l
(9.1) �g��
na =
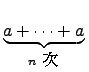
= (
)
. a = (
n1)
. a.
�� ��.
�Ҽ

:

 F
F �䤤

(0) = 0, �B����N
n 

,

(
n) =
n1,

(-
n) =
n(- 1). �Y
�`�N�o�̪� 1 �O
F ���� 1, �� -1 �O
F �� 1 ���[�k
inverse. �ܮe���ˬd

�O�@�ӱq

��
F �� ring
homomorphism.
��Ҽ  �� kernel. �� ring �� 1st isomorphism theorem (Theorem
6.4.2) �ڭ̦�
�� kernel. �� ring �� 1st isomorphism theorem (Theorem
6.4.2) �ڭ̦�
�M��
im(

) �|�O
F ���@�� subring (Lemma
6.3.3), �G��
F
�O integral domain (Lemma
9.1.1) ��
im(

) �]�O�@��
integral domain. ���y�ܻ�

/ker(

) �O�@�� integral domain.
�t�@�譱
ker(

) �|�O

���@�� ideal (Lemma
6.3.3)
�G�Q�� Theorem
6.5.7 ��
ker(

) �O

���@�� prime
ideal. �]

�O�@�� principle ideal domain, �G�s�b
a 

����
ker(

) =
 a
a
. �Q�� Lemma
8.1.9 �ڭ̪�
a = 0 ��
a =
p, �䤤
p �O

�����@�� prime.
(1)
ker( ) =
) =  0
0 ������: ���ɦ]����N��
n
������: ���ɦ]����N��
n 
 , �Ҧ�
n1
, �Ҧ�
n1 0 (�]
n
0 (�]
n  ker(
ker( )), �G������N�� a
)), �G������N�� a  F �B a
F �B a 0, �] F �O integral domain, �Ҧ�
0, �] F �O integral domain, �Ҧ�
na = (
n1)
. a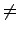
0.
(2)
ker( ) =
) =  p
p ������: ���ɦ]
p
������: ���ɦ]
p  ker(
ker( ), �ڭ̦�
p1 = 0. �G�o����N�� a
), �ڭ̦�
p1 = 0. �G�o����N�� a  F �Ҧ�
F �Ҧ�
pa = (p1) . a = 0.

�b Lemma 9.2.1 ���� 0 �� p �� field
�������W�O�ܭ��n��, �]���ڭ̦��H�U���w�q.
Definition 9.2.2
���]
F �O�@�� field. �Y����N��
n 

�B
a  F
F 
{0} �Ҧ�
na
0, �h��
F ��
characteristic �O
0. �O��
char(
F) = 0. �Ϥ��Y�s�b
p 

�O

���� prime
�ϱo����N��
a  F
F �Ҧ�
pa = 0, �h��
F ��
characteristic
�O
p. �O��
char(
F) =
p.
�Ҧp���z�ƩҦ��� field
 �� characteristic �N�O 0. �S�Ҧp�b
Example 9.1.3 ����
�� characteristic �N�O 0. �S�Ҧp�b
Example 9.1.3 ����
 /5
/5 �N�ŦX����N��
a
�N�ŦX����N��
a 
 /5
/5 �Ҧ� 5a = 0, �ҥH�ڭ̦�
char(
�Ҧ� 5a = 0, �ҥH�ڭ̦�
char( /5
/5 ) = 5.
) = 5.
�n�`�N�� Lemma 9.2.1 �ڭ̪��Y F �O�@�� field, �h
char(F)
�n���O���� 0 �N�O����@�� prime p. �p�G
char(F) = p 0, �h��
p �O���� pa = 0 �䤤
a
0, �h��
p �O���� pa = 0 �䤤
a  F
F  {0} ���̤p�������. �]���Y
n
{0} ���̤p�������. �]���Y
n 
 �B na = 0, �h�� F �O integral domain �H��
�B na = 0, �h�� F �O integral domain �H��
na = (n1) . a = 0
�� n1 = 0. �]�N�O��
n  ker(
ker( ) =
) =  p
p .
�o�i�D�ڭ� n
.
�o�i�D�ڭ� n p.
p.
�Y F �O�@�� field �B F �u�������h�Ӥ���, �h�ڭ̺� F ���@��
finite field.
Lemma 9.2.3
�Y
F �O�@�� finite field, �h�s�b�@ prime
p 

�ϱo
char(
F) =
p.
�� ��.
�� Lemma
9.2.1 �ڭ̪�
char(
F) = 0 ��
char(
F) =
p �䤤
p
�O�@�ӽ��. �ڭ̭n����
char(
F) ���i��O 0. ���p�G
char(
F) = 0,
���ܫe���w������ ring homomorphism

:

 F
F �ŦX
ker(

) =

0

, �]�N�O��

�O�@��@��. ������


im(

)
 F
F. �M��

���L�a�h�Ӥ���, �G�o��
F �����@�� subring �䤸�����L�a�h��. ���M
F �O finite field
�ۥ٬�, �G��
char(
F) =
p
0.

�Q�� Proposition 9.1.5 �ڭ̥i�o�H�U������ characteristic
���ʽ�. ���i�D�ڭ̷���� field �� characteristic ���ۦP��,
���̤������i��s�b nontrivial �� ring homomorphism.
Proposition 9.2.4
���]
F �M
F' �O fields �B
F �M
F' �����s�b nontrivial ��
ring homomorphism, �h
char(
F) = char(
F').
�� ��.
���]

:
F F'
F' ���O�@�� trivial �� ring homomorphism, ��
Proposition
9.1.5 (1) ��

(1
F) = 1
F'. �]���Y
char(
F) =
p
0, �Q��

(
p1
F) =

(0) = 0
�H��

(
p1
F) =

(
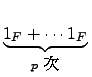
) =
p
(1
F) =
p1
F',
�ڭ̱o
p1F' = 0.
�G��
char(
F')

0. �M�ӭY
char(
F') =
q p
p, �h�]
p �M
q �ҬO��ƩҥH����, �G�s�b
m,
n 

�ϱo
mp +
nq = 1.
�]����
p1
F' =
q1
F' = 0 �i�o
1F' = (mp + nq)1F' = 0,
�y���٬�. �G��
char(
F) = char(
F').
�t� �Y
char(F) = 0, ���ɹ���N
n 
 �Ҧ� n1F
�Ҧ� n1F 0. �Q��
Proposition 9.1.5 (2) ��
0. �Q��
Proposition 9.1.5 (2) ��
 (n1F)
(n1F) 0. ���y�ܻ�
0. ���y�ܻ�
�o����
char(
F') = 0.

�̫�ڭ̨Ӭݷ�
char(F) = p 0 ��, �b�B��W���@�ӯS���ʽ�.
0 ��, �b�B��W���@�ӯS���ʽ�.
Lemma 9.2.5
���]
F �O�@�� field �B
char(
F) =
p
0, �h����N
a,
b  F
F,
�ڭ̦�
(
a +
b)
pn =
apn +
bpn and (
a -
b)
pn =
apn -
bpn,
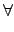 n
n 
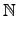
.
�� ��.
�ڭ̥��� induction �ҩ�
(
a +
b)
pn =
apn +
bpn. �����Ҽ
n = 1 �����p. �ڭ̥��ˬd (
a +
b)
2 ����? �ѩ�
(
a +
b)
2 =
a2 +
a . b +
b . a +
b2, �Q��
F �O�@�� field ��
a . b =
b . a,
�]���ڭ̱o
(
a +
b)
2 =
a2 + 2(
a . b) +
b2. �A���j�ճo��
2(
a . b)
�O
(
a . b) + (
a . b) �Ӥ��O
2
. (
a . b).
�ҥH� ��U�h�ڭ̥i�H�Q�������G�����w�z�o
(
a +
b)
p =
ap +
p(
ap - 1 . b) +
... +
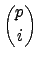
(
ai . bp - i) +
... +
bp.
�ѩ�
char(
F) =
p, ����N

 F
F,

�ۤv�s�[�ۤv
p ������ 0 (�Y
p
= 0). �j�a�����D��
p �O��ƥB��
i = 1,...,
p - 1 ��,
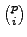
�O
p ������,
�G������
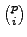
(
ai . bp - i) = 0. �]���ڭ̥i�o
| (a + b)p = ap + bp. |
(9.2) |
��Q���k�ǰ��]
| (a + b)pn - 1 = apn - 1 + bpn - 1, |
(9.3) |
�G�Q���l (
9.2)
�M (
9.3) �ڭ̪�
(a + b)pn = 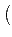 (a + b)pn - 1 (a + b)pn - 1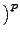 = (apn - 1 + bpn - 1)p = apn + bpn. = (apn - 1 + bpn - 1)p = apn + bpn. |
|
���U���ҩ�
(a - b)pn = apn - bpn. �����`�N��
char(F) = 2 ��,
����N

 F �ڭ̦�
F �ڭ̦�
 +
+  = 2
= 2 = 0, �G��
= 0, �G��
 = -
= -  . �]���b p = 2 �ɧڭ̦۵M��
. �]���b p = 2 �ɧڭ̦۵M��
(a - b)pn = (a + b)pn = apn + bpn = apn - bpn.
�ӷ�
p �O odd prime number ��, �ѩ����N

�Ҧ�
(-

)
pn = -
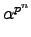
(Corollary
5.2.4), �ڭ̱o
(
a -
b)
pn =
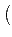 a
a + (-
b)
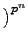
=
apn + (-
b)
pn =
apn -
bpn.

Lemma 9.2.5 �]�i�H���s�� F[x] �W���B��. �`�N F[x] �W��
polynomial ���Y�Ƴ��b F ��, �ӥB F[x]
�W���[�k�̩w�q�O�N�P�������Y�Ƴ��[�_��. �]���Y
char(F) = p ��,
����N��
f (x) = anxn + ... + a0  F[x] �ڭ̳���
F[x] �ڭ̳���
�]���Q������ Lemma 9.2.5 ���ҩ��ڭ̦��H�U���ʽ�:
Lemma 9.2.6
���]
F �O�@�� field �B
char(
F) =
p
0, �h����N
f (
x) =
amxm +
... +
a0  F
F[
x], �ڭ̦�
(
f (
x))
pn =
ampnxmpn +
... +
a0pn,
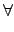 n
n 
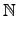
.
�S�O��
a  F
F ��, �ڭ̦�
(
x -
a)
pn =
xpn -
apn,
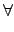 n
n 
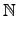
.



�U�@��: �u�ʥN�ƪ�����
�W�@��: ��� Field ���ʽ�
�e�@��: Field ���ʽ�
Administrator
2005-06-18
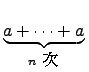 = (
= (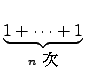 ) . a.
) . a.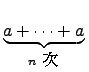 = n . a.
= n . a.
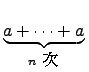 = na.
= na.
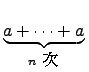 = (
= (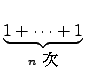 ) . a = (n1) . a.
) . a = (n1) . a.
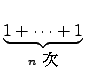 �B
�B 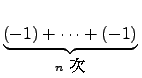 .
.
![]() �� kernel. �� ring �� 1st isomorphism theorem (Theorem
6.4.2) �ڭ̦�
�� kernel. �� ring �� 1st isomorphism theorem (Theorem
6.4.2) �ڭ̦�
![]() ) =
) = ![]() 0
0![]() ������: ���ɦ]����N��
n
������: ���ɦ]����N��
n ![]()
![]() , �Ҧ�
n1
, �Ҧ�
n1![]() 0 (�]
n
0 (�]
n ![]() ker(
ker(![]() )), �G������N�� a
)), �G������N�� a ![]() F �B a
F �B a![]() 0, �] F �O integral domain, �Ҧ�
0, �] F �O integral domain, �Ҧ�
![]() ) =
) = ![]() p
p![]() ������: ���ɦ]
p
������: ���ɦ]
p ![]() ker(
ker(![]() ), �ڭ̦�
p1 = 0. �G�o����N�� a
), �ڭ̦�
p1 = 0. �G�o����N�� a ![]() F �Ҧ�
F �Ҧ�
![]() �� characteristic �N�O 0. �S�Ҧp�b
Example 9.1.3 ����
�� characteristic �N�O 0. �S�Ҧp�b
Example 9.1.3 ����
![]() /5
/5![]() �N�ŦX����N��
a
�N�ŦX����N��
a ![]()
![]() /5
/5![]() �Ҧ� 5a = 0, �ҥH�ڭ̦�
char(
�Ҧ� 5a = 0, �ҥH�ڭ̦�
char(![]() /5
/5![]() ) = 5.
) = 5.
![]() 0, �h��
p �O���� pa = 0 �䤤
a
0, �h��
p �O���� pa = 0 �䤤
a ![]() F
F ![]() {0} ���̤p�������. �]���Y
n
{0} ���̤p�������. �]���Y
n ![]()
![]() �B na = 0, �h�� F �O integral domain �H��
�B na = 0, �h�� F �O integral domain �H��
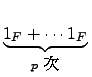 ) = p
) = p![]()
![]() �Ҧ� n1F
�Ҧ� n1F![]() 0. �Q��
Proposition 9.1.5 (2) ��
0. �Q��
Proposition 9.1.5 (2) ��
![]() (n1F)
(n1F)![]() 0. ���y�ܻ�
0. ���y�ܻ�
![]() 0 ��, �b�B��W���@�ӯS���ʽ�.
0 ��, �b�B��W���@�ӯS���ʽ�.
![]()
![]() F �ڭ̦�
F �ڭ̦�
![]() +
+ ![]() = 2
= 2![]() = 0, �G��
= 0, �G��
![]() = -
= - ![]() . �]���b p = 2 �ɧڭ̦۵M��
. �]���b p = 2 �ɧڭ̦۵M��
![]() F[x] �ڭ̳���
F[x] �ڭ̳���
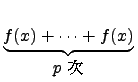 = (
= (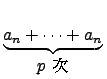 )xn + ... + (
)xn + ... + (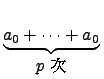 ) = 0.
) = 0.