


下一頁: Sylow p-subgroups 的個數
上一頁: Third Sylow's Theorem
前一頁: Third Sylow's Theorem
若 G 是一個 finite group, p 是一個整除 | G| 的質數. 令 S 為
G 中所有的 Sylow p-subgroup 所成的集合 (也就是每個 Sylow
p-subgroup 都看成是 S 的一個元素). 我們要介紹兩種 group action,
一個是將 G 作用在 S 上. 另一個是選定 G 中任一個 Sylow
p-subgroup P 而考慮 P 對 S 的作用.
我們定義 G 對 S 的作用如下: 對任意 a  G, P'
G, P'  S, 我們定義
S, 我們定義
a*P' = a . P' . a-1.
我們證明 (G, S,*) 是一個 group action. 首先證明 (Act1). 因 P' 是
G 的 Sylow p-subgroup, 前面已提過 Lemma 1.5.2 告訴我們
a . P' . a-1 也是 G 的 Sylow p-subgroup. 故得
a*P'  S. 而
e*P' = e . P' . e-1 = P' 故 (Act2) 也成立.
最後若 a, b
S. 而
e*P' = e . P' . e-1 = P' 故 (Act2) 也成立.
最後若 a, b  G, 因為
G, 因為
(a . b)*P' = (a . b) . P' . (a . b)-1 = (a . b) . P' . (b-1 . a-1),
且
a*(b*P') = a . (b*P') . a-1 = a . (b . P' . b-1) . a-1,
故由結合率知
(a . b)*P' = a*(b*P').
這證明了 (Act3).
| S| 是什麼呢? 無庸置疑的就是 G 中所有 Sylow p-subgroup 的個數.
這裡我們並不關心 S0 是什麼, 主要原因在這個 group action
之下只分成一類, 所以我們可以直接計算 | S|.
為什麼只分成一類呢? 任選
P1, P2  S 由第二 Sylow 定理 (Theorem
4.5.1) 我們知存在 a
S 由第二 Sylow 定理 (Theorem
4.5.1) 我們知存在 a  G 使得
G 使得
P2 = a . P1 . a-1 = a*P1.
換句話說任選 S 中的兩元素都是同類的,
所以在此分類之下當然只有一類了. 現在我們任取一 P'  S, 由式子
(4.1) 知
| S| = |[P']|. 所以我們只要算 [P'] 有多少就可以了.
Lemma 4.1.3 告訴我們
|[P']| = | G|/| GP'|, 其中
GP' = {a
S, 由式子
(4.1) 知
| S| = |[P']|. 所以我們只要算 [P'] 有多少就可以了.
Lemma 4.1.3 告訴我們
|[P']| = | G|/| GP'|, 其中
GP' = {a  G | a*P' = P'}. GP' 到底是什麼呢?
由定義知任何 GP' 中的元素 a 皆須滿足
G | a*P' = P'}. GP' 到底是什麼呢?
由定義知任何 GP' 中的元素 a 皆須滿足
P' = a*P' = a . P' . a-1.
如果大家還不健忘的話該記得我們曾在 4.4 節中介紹過這樣的元素所成的集合
就是 P' 的 normalizer N(P'). 所以我們知
GP' = N(P').
因此我們可得
| S| = |[P']| = 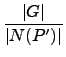 |
(4.19) |
現在我們介紹另一個類似的 group action. 選定 G 中任一個 Sylow
p-subgroup P, 我們定義 P 對 S (和前面同樣的 S) 的作用如下:
對任意 x  P, P'
P, P'  S, 我們定義
S, 我們定義
x*P' = x . P' . x-1.
這個作用和前一個幾乎相同,
只是我們拿比較小的 group 去作用. 不難看出 (P, S,*) 也是一個 group
action.
同樣的 S 的個數仍是所有 G 的 Sylow p-subgroup 的個數.
要注意的是這次我們作用的 group 比較小, 所以同類的元素會比較少,
因此前一次所得只分成一類的結果這兒並不一定對. 這一次我們需要算
| S0|.
S0 是什麼呢? 由定義若 P'  S0, 表示對所有 x
S0, 表示對所有 x  P,
P,
x . P' . x-1 = x*P' = P',
由 normalizer 的定義知這表示
x  N(P').
換句話說若 P'
N(P').
換句話說若 P'  S0 則 P' 必須具有對所有 x
S0 則 P' 必須具有對所有 x  P 皆可得
x
P 皆可得
x  N(P') 的性質. 也就是說: 若 P'
N(P') 的性質. 也就是說: 若 P'  S0, 則
P
S0, 則
P  N(P').
反之, 若 P' 是 G 的一個 Sylow p-subgroup 且符合
P
N(P').
反之, 若 P' 是 G 的一個 Sylow p-subgroup 且符合
P  N(P'), 則對任意的 x
N(P'), 則對任意的 x  P, 皆有 x*P' = P'.
所以我們證得
P, 皆有 x*P' = P'.
所以我們證得
S0 = {P'  S | P S | P 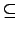 N(P')}. N(P')}. |
(4.20) |
最後我們強調因 P  S 且 Lemma 4.4.1 告訴我們
P
S 且 Lemma 4.4.1 告訴我們
P  N(P), 故知
N(P), 故知
P  S0. S0. |
(4.21) |



下一頁: Sylow p-subgroups 的個數
上一頁: Third Sylow's Theorem
前一頁: Third Sylow's Theorem
Administrator
2005-06-18
![]() G, P'
G, P' ![]() S, 我們定義
S, 我們定義
![]() S. 而
e*P' = e . P' . e-1 = P' 故 (Act2) 也成立.
最後若 a, b
S. 而
e*P' = e . P' . e-1 = P' 故 (Act2) 也成立.
最後若 a, b ![]() G, 因為
G, 因為
![]() S 由第二 Sylow 定理 (Theorem
4.5.1) 我們知存在 a
S 由第二 Sylow 定理 (Theorem
4.5.1) 我們知存在 a ![]() G 使得
G 使得
![]() P, P'
P, P' ![]() S, 我們定義
S, 我們定義
![]() S0, 表示對所有 x
S0, 表示對所有 x ![]() P,
P,