


�U�@��: Prime ideals
�W�@��: �S���� Ideals
�e�@��: �S���� Ideals
�b group ���ڭ̤��йL cyclic subgroup,
���i�H�O���]�t�Y�@�Ӥ������̤p�� subgroup. �b ring ���ڭ̤]���ҿת�
principle ideal, ���O�]�t�Y�@�������̤p�� ideal.
���] R �O�@�� commutative ring with 1. �n�F�� R ���� ideal
���ƻ�ˤl, �ڭ̭����|�Ҽ�]�t�Y�@�������̤p�� ideal ����,
�]���o�O��²�檺 ideal. �Y���w a  R, �h�]�t a ���̤p ideal I
���Ӫ��ƻ�ˤl�O? ���� I �ܤ֭n�]�t a �Ҳ��ͪ��[�k�� cyclic
group, �Y
{0, a, - a, 2a, - 2a,..., na, - na,...}. �`�N�e�����L�o��
2a ���O 2 . a �ӬO
(1 + 1) . a (�O�ѤF 1
R, �h�]�t a ���̤p ideal I
���Ӫ��ƻ�ˤl�O? ���� I �ܤ֭n�]�t a �Ҳ��ͪ��[�k�� cyclic
group, �Y
{0, a, - a, 2a, - 2a,..., na, - na,...}. �`�N�e�����L�o��
2a ���O 2 . a �ӬO
(1 + 1) . a (�O�ѤF 1  R �o�Ӱ��]).
�ѩ� 1 + 1
R �o�Ӱ��]).
�ѩ� 1 + 1  R, �ڭ̥i�H���s�b�Y�@����
R, �ڭ̥i�H���s�b�Y�@����

 R �ϱo
2a =
R �ϱo
2a =  . a. �P�z���L������� n, �ѩ�
. a. �P�z���L������� n, �ѩ�
na =
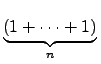 . a
. a
�ҥH (���� 1  R
�o�Ӱ��]) �s�b
R
�o�Ӱ��]) �s�b
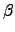
 R ����
na =
R ����
na = 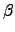 . a. �t�@�譱�� Lemma
6.1.2, �� I ���]�����]�t����N�� r
. a. �t�@�譱�� Lemma
6.1.2, �� I ���]�����]�t����N�� r  R, r . a �M
a . r �o�ؤ���. �M��
r . a = a . r (���� R �O
commutative ring �o�Ӱ��]), �]�� I ���ܤ֭n�]�t�Ҧ��� r . a
�o�اΦ�������. �p�G�ѩҦ��� r . a �o�˪������Ҧ������X�O R
���@�� ideal, ���۵M�N�O�]�t a ���̤p ideal �F.
R, r . a �M
a . r �o�ؤ���. �M��
r . a = a . r (���� R �O
commutative ring �o�Ӱ��]), �]�� I ���ܤ֭n�]�t�Ҧ��� r . a
�o�اΦ�������. �p�G�ѩҦ��� r . a �o�˪������Ҧ������X�O R
���@�� ideal, ���۵M�N�O�]�t a ���̤p ideal �F.
Lemma 6.5.1
���]
R �O�@�� commutative ring with 1, �B
a  R
R. �O
A = {
r . a |
r  R
R}, �h
A �O
R ���@�� ideal. �ƹ�W,
A
�O
R ���]�t
a ���̤p�� ideal.
�� ��.
�q�e�����Q�קڭ̤w��: �Y
I �O
R ���]�t
a ���̤p�� ideal, �h
A  I
I. �]���Y���ұo
A �O
R �� ideal, �h��
I =
A.
�ڭ̧Q�� Lemma 6.1.2 ���ҩ� A �O R �� ideal. ���� A
���⤸�� r . a �M r' . a, �䤤 r, r'  R. �ѩ�
r . a - r' . a = (r - r') . a �B r - r'
R. �ѩ�
r . a - r' . a = (r - r') . a �B r - r'  R, ��
r . a - r' . a
R, ��
r . a - r' . a  A. �t� ���� R ���@���� r �� A ���@���� r' . a, �䤤
r'
A. �t� ���� R ���@���� r �� A ���@���� r' . a, �䤤
r'  R. �ѩ�
(r' . a) . r = r . (r' . a) = (r . r') . a �B
r . r'
R. �ѩ�
(r' . a) . r = r . (r' . a) = (r . r') . a �B
r . r'  R, ��
(r' . a) . r = r . (r' . a)
R, ��
(r' . a) . r = r . (r' . a)  A. �]�� A �O R �� ideal.
A. �]�� A �O R �� ideal.

�q�`�ڭ̷|�N Lemma 6.5.1 ���� A ��
 a
a �Ӫ���.
�`�N�ڭ̬O�Τj�@�I���A��
�Ӫ���.
�`�N�ڭ̬O�Τj�@�I���A��

 �H�K�M�@��B�ⶡ���p�A��
( ) �V�c.
�H�K�M�@��B�ⶡ���p�A��
( ) �V�c.
Definition 6.5.2
���]
R �O�@�� commutative ring with 1, �B
a  R
R. �h
�٬� the
principle ideal
generated by
a in
R. �Y
I ��
R ���@�� ideal �B�b
R
���s�b�@����
a ����
I =
 a
a
�h��
I �O
R ���@��
principle ideal.
Example 6.5.3
�b

��, ����
n 

, �h�Ҧ�
n �����ƩҦ������X�O�@��
principle ideal, �Y
 n
n
= {
z . n |
z 

}.
�N�ӧڭ̷|�ݨ�b
 ���Ҧ��� ideal ���O principle ideal,
���L�o��@�몺 ring �ä��@�w��. �t� �Y I �O�@�� principle ideal,
�ä����ܲ��� I �������O�ߤ@�� (�Ҧp�e�����Ҥl�ڭ̦�
���Ҧ��� ideal ���O principle ideal,
���L�o��@�몺 ring �ä��@�w��. �t� �Y I �O�@�� principle ideal,
�ä����ܲ��� I �������O�ߤ@�� (�Ҧp�e�����Ҥl�ڭ̦�
 n
n =
=  - n
- n ), �ƹ�W�ڭ̦��H�U�����G.
), �ƹ�W�ڭ̦��H�U�����G.
Lemma 6.5.4
���]
R �O�@�� commutative ring with 1. �p�G
a,
b  R
R �B
�s�b�@ unit
u  R
R ����
a =
u . b, �h
 a
a
=
 b
b
.
�� ��.
�ѩ�
a =
u . b, �ѩw�q��
a 
 b
b
. �S�ѩ�
 b
b
�O�@�� ideal �B
 a
a
�O�]�t
a �̤p��
ideal, �G�o
 a
a

 b
b
. �Ϥ�, �]
u �O
R �� unit, �G�s�b
v  R
R ����
v . u = 1. �ҥH��
b = (
v . u)
. b =
v . a ��
b 
 a
a
. �A�Q��
 b
b
�O�]�t
b �̤p�� ideal �o
 b
b

 a
a
.
�G�ұo
 a
a
=
 b
b
.

�H�U���Ф@�� principle ideal ��²������. �ڭ̦b lemma 6.2.4
�����D: �� R �O�@�� division ring ��, R ���u�� {0} �M R
�o��� ideals. �� R �O�@�� field �� (R �]�N�O�@�� division
ring), R ���M�]�N�S�� nontrivial proper ideal. �� R �O
commutative ring with 1 ��, �o�O�@�����U�ڭ̧P�_ R �O�_���@��
field ���n��k.
Proposition 6.5.5
�Y
R �O�@�� commutative ring with 1, �h
R �O�@�� field
�Y�B�߭Y
R �S�� nontrivial proper ideal.
�� ��.
�ڭ̤w����
R �O�@�� field ��,
R �S�� nontrivial proper ideal.
�Ϥ�, �p�G
R �S�� nontrivial proper ideal, �ڭ̷Q�ҩ�
R �O�@��
field. �ѩ�
R �w���]�O commutative ring with 1,
�̩w�q�ڭ̥u�n�ҩ�
R ���D 0 ���������O unit. ����
a  R
R �B
a
0. �ڭ̦Ҽ
 a
a
�o�@�� principle ideal. �]��
a
0 �B
a 
 a
a
, �G��
 a
a

{0}.
���L�̰��]
R �����F {0} �M
R �w� �S����L�� ideal, �]���o
 a
a
=
R. �M�� 1
 R
R, �Y
1

 a
a
�G��
 a
a
���w�q���s�b
r  R
R �ϱo
1 =
r . a. �]�N�O��
a �O�@�� unit.

�̫�ڭ̭n�j��, �b Proposition 3.1.3 ���ڭ̪��D�@�� cyclic
group ���� subgroup ���O cyclic group. ���L�� principle ideal,
�o�N���@�w��F. �]�N�O���Y I, I' ���O R �� ideal �B
I'  I. �p�G�w�� I �O principle ideal, �o��O�� I'
�|�O principle ideal.
I. �p�G�w�� I �O principle ideal, �o��O�� I'
�|�O principle ideal.



�U�@��: Prime ideals
�W�@��: �S���� Ideals
�e�@��: �S���� Ideals
Administrator
2005-06-18
![]() R, �h�]�t a ���̤p ideal I
���Ӫ��ƻ�ˤl�O? ���� I �ܤ֭n�]�t a �Ҳ��ͪ��[�k�� cyclic
group, �Y
{0, a, - a, 2a, - 2a,..., na, - na,...}. �`�N�e�����L�o��
2a ���O 2 . a �ӬO
(1 + 1) . a (�O�ѤF 1
R, �h�]�t a ���̤p ideal I
���Ӫ��ƻ�ˤl�O? ���� I �ܤ֭n�]�t a �Ҳ��ͪ��[�k�� cyclic
group, �Y
{0, a, - a, 2a, - 2a,..., na, - na,...}. �`�N�e�����L�o��
2a ���O 2 . a �ӬO
(1 + 1) . a (�O�ѤF 1 ![]() R �o�Ӱ��]).
�ѩ� 1 + 1
R �o�Ӱ��]).
�ѩ� 1 + 1 ![]() R, �ڭ̥i�H���s�b�Y�@����
R, �ڭ̥i�H���s�b�Y�@����
![]()
![]() R �ϱo
2a =
R �ϱo
2a = ![]() . a. �P�z���L������� n, �ѩ�
. a. �P�z���L������� n, �ѩ�
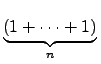 . a
. a
![]() R. �ѩ�
r . a - r' . a = (r - r') . a �B r - r'
R. �ѩ�
r . a - r' . a = (r - r') . a �B r - r' ![]() R, ��
r . a - r' . a
R, ��
r . a - r' . a ![]() A. �t� ���� R ���@���� r �� A ���@���� r' . a, �䤤
r'
A. �t� ���� R ���@���� r �� A ���@���� r' . a, �䤤
r' ![]() R. �ѩ�
(r' . a) . r = r . (r' . a) = (r . r') . a �B
r . r'
R. �ѩ�
(r' . a) . r = r . (r' . a) = (r . r') . a �B
r . r' ![]() R, ��
(r' . a) . r = r . (r' . a)
R, ��
(r' . a) . r = r . (r' . a) ![]() A. �]�� A �O R �� ideal.
A. �]�� A �O R �� ideal.
![]()
![]() a
a![]() �Ӫ���.
�`�N�ڭ̬O�Τj�@�I���A��
�Ӫ���.
�`�N�ڭ̬O�Τj�@�I���A��
![]()
![]() �H�K�M�@��B�ⶡ���p�A��
( ) �V�c.
�H�K�M�@��B�ⶡ���p�A��
( ) �V�c.
![]() ���Ҧ��� ideal ���O principle ideal,
���L�o��@�몺 ring �ä��@�w��. �t� �Y I �O�@�� principle ideal,
�ä����ܲ��� I �������O�ߤ@�� (�Ҧp�e�����Ҥl�ڭ̦�
���Ҧ��� ideal ���O principle ideal,
���L�o��@�몺 ring �ä��@�w��. �t� �Y I �O�@�� principle ideal,
�ä����ܲ��� I �������O�ߤ@�� (�Ҧp�e�����Ҥl�ڭ̦�
![]() n
n![]() =
= ![]() - n
- n![]() ), �ƹ�W�ڭ̦��H�U�����G.
), �ƹ�W�ڭ̦��H�U�����G.
![]() I. �p�G�w�� I �O principle ideal, �o��O�� I'
�|�O principle ideal.
I. �p�G�w�� I �O principle ideal, �o��O�� I'
�|�O principle ideal.