將 ring 看成是 vector space

假設 F 是一個 field, 我們考� F[x] 這一個 polynomial ring. 很容易看出來 F[x] 和 F 滿足 Definition 9.3.1 中 (VS1) 到 (VS4) 性質, 故知 F[x] 是一個 vector space over F. 至於 F[x] 會不會是 finite dimensional vector space over F 呢?

証明. 我們利用反證法. 假設 F[x] 是 finite dimensional over F 且 dim_F(F[x]) = n, 則考� 1, x, x²,..., xⁿ $\in$ F[x], 我們要驗證 1, x, x²,..., xⁿ 是 linearly independent over F. 這是因為對任意不全為 0 的 c₀, c₁,..., c_n 我們知

c₀^.1 + c₁^.x + ^... + c_n^.xⁿ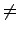 $\displaystyle \ne$ 0.

注意 1, x, x²,..., xⁿ 共有 n + 1 個元素, 故利用 Lemma 9.3.4 (2) 知

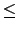
n + 1 $\displaystyle \le$ dim_F(F[x]) = n,

因而得到矛盾. 所以 F[x] 不可能是 finite dimensional over F. $\qedsymbol$

接著我們考憧t一個 ring. 假設 f (x) $\in$ F[x] 且 deg(f (x)) $\ge$ 1, 我們考� R = F[x]/ $\bigl($ f (x) $\bigr)$ 這一個 quotient ring. 回顧一下 R 中的元素都是 $\overline{g(x)}$ 的形式, 其中 g(x) $\in$ F[x]. 對任意的 c $\in$ F, $\overline{g(x)}$ $\in$ R, 我們定義

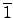
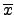
証明. 假設 deg(f (x)) = n, 我們要證明 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ $\in$ R 是 R over F 的一組 basis.

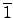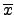首先證明 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ span R over F. 任取 $\overline{g(x)}$ $\in$ R, 其中 g(x) $\in$ F[x], 我們要找到 c₀, c₁,..., c_{n - 1} $\in$ F 使得

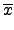
$\displaystyle \overline{g(x)}$ = c₀^. $\displaystyle \overline{1}$ + c₁^. $\displaystyle \overline{x}$ + ^... + c_{n - 1}^. $\displaystyle \overline{x}^{n-1}_{}$ .

由 Theorem 7.2.4, 我們知道存在 h(x), r(x) $\in$ F[x] 滿足 g(x) = f (x)^.h(x) + r(x), 其中 r(x) = 0 或 deg(r(x)) < deg(f (x)). 因為 g(x) - r(x) = f (x)^.h(x) $\in$ $\bigl($ f (x) $\bigr)$ , 由 quotient ring 的定義知 $\overline{g(x)}$ = $\overline{r(x)}$ . 痍Y r(x) = 0, 知 $\overline{g(x)}$ = $\overline{0}$ , 故取 c₀ = c₁ = ^... = c_{n - 1} = 0 時可得

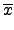
$\displaystyle \overline{g(x)}$ = $\displaystyle \overline{0}$ = c₀^. $\displaystyle \overline{1}$ + c₁^. $\displaystyle \overline{x}$ + ^... + c_{n - 1}^. $\displaystyle \overline{x}^{n-1}_{}$ .

另一方面若 r(x) $\ne$ 0, 則由 deg(r(x)) $\le$ n - 1 知存在 a₀, a₁,..., a_{n - 1} $\in$ F 使得 r(x) = a₀ + a₁x + ^... + a_{n - 1}x^{n - 1}, 故令 c₀ = a₀,..., c_{n - 1} = a_{n - 1} 時我們有

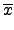
$\displaystyle \overline{g(x)}$ = $\displaystyle \overline{r(x)}$ = c₀^. $\displaystyle \overline{1}$ + c₁^. $\displaystyle \overline{x}$ + ^... + c_{n - 1}^. $\displaystyle \overline{x}^{n-1}_{}$ .

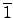
所以 R 中的元素都可由 $\overline{1}$ ,..., $\overline{x}^{n-1}_{}$ span over F 得到.

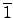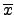接著證明 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ 是 linearly independent over F. 我們利用反證法. 假設存在不全為 0 的 c₀, c₁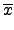,^..., c_{n - 1} $\in$ F 使得

c₀^. $\displaystyle \overline{1}$ + c₁^. $\displaystyle \overline{x}$ + ^... + c_{n - 1}^. $\displaystyle \overline{x}^{n-1}_{}$ = $\displaystyle \overline{0}$ ,

表示 g(x) = c₀ + ^... + c_{n - 1}x^{n - 1} 這個非 0 的多項式符合 $\overline{g(x)}$ = $\overline{0}$ . 換句話說 g(x) $\in$ $\bigl($ f (x) $\bigr)$ . 因 g(x) $\ne$ 0, 故知存在 h(x) $\in$ F[x] 且 h(x) $\ne$ 0 使得 g(x) = f (x)^.h(x). 觀察 degree 知

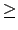
deg(g(x)) = deg(f (x)) + deg(h(x)) $\displaystyle \ge$ deg(f (x)) = n,

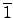
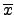
不過由當初 g(x) 的選取, 我們知道 deg(g(x)) $\le$ n - 1, 因此得到矛盾. 故知 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ 是 linearly independent over F.

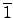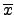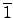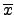我們已證得 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ $\in$ R 是 R over F 的一組 basis. 又因 $\overline{1}$ , $\overline{x}$ ,..., $\overline{x}^{n-1}_{}$ 中共有 n 個元素, 故知 dim_F(R) = n = deg(f (x)). $\qedsymbol$

當 R 是一個 integral domain 且 F 是一個包含於 R 的 field 時, 我們也可以將 R 看成是一個 vector space over F. 事實上由 ring 的性質加上 F $\subseteq$ R, Definition 9.3.1 中的 (VS1), (VS2) 以及 (VS3) 自然都符合, 我們唯一要檢查的是 (VS4). 假設 1_F, 1_R 分別是 F 和 R 乘法的 identity, 我們只要檢察 1_F = 1_R 即可. 這是因為 (VS4) 是說對任意的 a $\in$ R 要符合 1_F^.a = a. 因此若能證得 1_F = 1_R, 那麼上式自然成立. 要注意我們曾經看過例子一個 subring 的 identity 不一定會是原來的 ring 的 identity. 不過由於畢b R 是 integral domain, 事情就沒有那麼複雜了. 我們只要任取 F 中的一個非 0 元素 c, 將它考憐足O F 的元素, 我們有 1_F^.c = c; 另一方面將它看成是 R 的元素, 我們有 1_R^.c = c. 結合上面兩個等式得: (1_F - 1_R)^.c = 0. 由於 R 是 integral domain 且 c $\ne$ 0, 所以我們有 1_F = 1_R.

既然 R 是一個 over F 的 vector space, 我們來看當 R 是 finite dimensional over F 時它有什麼重要特性.

証明. 我們假設 dim_F(R) = n.

(1) 考� 1, a, a²,..., aⁿ 這 n + 1 個 R 中的元素. 如果它們是 linearly independent over F, 則由 Lemma 9.3.4 (2) 得

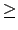n = dim_F(R) $\displaystyle \ge$ n + 1,

造成矛盾, 故知 1, a, a²,..., aⁿ 不是 linearly independent over F. 換句話說存在不全為 0 的 c₀, c₁,..., c_n $\in$ F, 滿足

c₀^.1 + c₁^.a + ^... + c_n^.aⁿ = 0.

故令 f (x) = c₀ + c₁x + ^... + c_nxⁿ, 我們得 f (x) $\ne$ 0 且 f (a) = 0.

(2) 因 R 已知是 integral domain, 要證明 R 是一個 field, 我們只要證明 R 中不為 0 的元素都是 unit. 換句話說要證明對任意 a $\in$ R 且 a $\ne$ 0, 皆存在 b $\in$ R 滿足 a^.b = 1. 由 (1) 知存在非 0 的多項式 f (x) 滿足 f (a) = 0. 我們假設

f (x) = c₀ + c₁x + ^... + c_mx^m $\displaystyle \in$ F[x]

是 F[x] 中非 0 且滿足 f (a) = 0 的 degree 最小的 polynomial. 由 degree 最小的假設, 我們可得 c₀ $\ne$ 0. 這是因為若 c₀ = 0, 則由

f (a) = c₁^.a + ^... + c_m^.a^m = (c₁ + c₂^.a + ^... + c_m^.a^{m - 1})^.a = 0

以及 R 是 integral domain 得 g(a) = 0, 其中 g(x) = c₁ + c₂x + ^... + c_mx^{m - 1} $\in$ F[x] 不為 0 且 deg(g(x)) < deg(f (x)). 此和 f (x) 是 degree 最小的找法相矛盾, 故得 c₀ $\ne$ 0. 盛N f (a) = 0 的 c₀ 移至等式的另一邊, 我們得

(c₁ + c₂^.a + ^... + c_m^.a^{m - 1})^.a = - c₀.

因此若令

b = (- c₀)^{-1 .}(c₁ + c₂^.a + ^... + c_m^.a^{m - 1}),

則我們有 a^.b = 1. 注意由於 - c₀ $\in$ F 且 - c₀ $\ne$ 0 以及 F 是一個 field, 我們有 (- c₀)^-1 $\in$ F $\subseteq$ R, 再加上 c₁ + c₂^.a + ^... + c_m^.a^{m - 1} $\in$ R 我們得 b $\in$ R, 故知 a 是 R 的一個 unit. $\qedsymbol$

利用 Theorem 9.3.7 我們可以很快的給 Proposition 9.3.5 另一個證明: 假如 F[x] 是 finite dimensional over F, 由於 F[x] 是 integral domain 利用 Theorem 9.3.7 我們得 F[x] 會是一個 field. 但這是不可能的, 因為 F[x] 中只有 degree 為 0 的元素� 是 unit.