


�U�@��: ���� Field ���ʽ�
�W�@��: ��� Field ���ʽ�
�e�@��: �N ring �ݦ��O vector
���w�@�� field F, �ڭ̷��M�i�H�Q�ר� subfield, ���L�]�@�� field
���z�����ߪ��O���w
f (x)  F[x] �p�G�b F �� f (x) �S����,
����p��b�� F �j�� field ����. �ҥH�ڭ̤�����ߪ��N�O�ҿ� F
�� extension field.
F[x] �p�G�b F �� f (x) �S����,
����p��b�� F �j�� field ����. �ҥH�ڭ̤�����ߪ��N�O�ҿ� F
�� extension field.
Definition 9.4.1
���w
F �O�@�� field, �Y
L 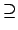 F
F �]�O�@�� field �ӥB
L
���B�⭭��b
F ���N�O�쥻
F ���B��, �h�ڭ̺�
L �O
F ���@��
extension (�κ�
extension field). ���M�F�ڭ̤]�i�H��
F
�O
L ���@��
subfield.
���] F �O�@�� field �B L �O F ���@�� extension field, �� Lemma
9.1.1 �� L �O�@�� integral domain, �G�ѫe�@�`���Q�קڭ̪�
L �O�@�� vector space over F. �ڭ̷��M�i�H�Q�� L over F ��
dimension.
Definition 9.4.2
���] F �O�@�� field �B L �O F ���@�� extension field. �p�G�N
L �ݦ��O over F ���@�� vector space �O�@�� finite dimensional
vector space over F, �h�� L �O F ���@�� finite
extension. �q�`�ڭ̷|�N dimF(L) �� [L : F] �Ӫ���, �٤��� the
degree of L over F (�Ӥ��O�� the dimension of L over
F).
�ڭ̥i�H�Q�� Theorem 9.3.7 �o��H�U���쪺���G:
Proposition 9.4.3
���]
F �O�@�� field �B
L �O
F ���@�� finite extension. �p�G
R �O
L ���@�� subring �B�ŦX
F  R
R  L
L, �h
R
�O�@�� field.
�� ��.
�ڭ̤�����Ωw�q�����ҩ�
R �O�@�� field, �ӬO�Q�M�� Theorem
9.3.7 �ӱo��. �n�M�� Theorem
9.3.7, �ڭ̥�������
R
�O�@�� integral domain �B dim
F(
R) �O������.
�]�� L �w�g�O�@�� integral domain (Lemma 9.1.1), �� R �O
L �� subring, �ҥH R ���M�O integral domain. �t�@�譱,
�ڭ̥i�H�� R �ݦ��O L ���@�� subspace over F. �G�Q�� L �O
F ���@�� finite extension �����]�H�� Lemma 9.3.4 ��
dimF(R) dimF(L), ���y�ܻ� R �O�@�� finite dimensional
vector space over F. �]���Q�� Theorem 9.3.7 (2) �o�� R
�O�@�� field.
dimF(L), ���y�ܻ� R �O�@�� finite dimensional
vector space over F. �]���Q�� Theorem 9.3.7 (2) �o�� R
�O�@�� field.

�Y L �O F ���@�� finite extension, �h�����N Theorem
9.3.7 (1) �M�Φb L �W, �ڭ̰��W������N�� a  L
�Ҧs�b�@�� F[x] ���� polynomial f (x)
L
�Ҧs�b�@�� F[x] ���� polynomial f (x) 0 ���� f (a) = 0.
�o�˪������ڭ̵����@�ӯS�����W�r.
0 ���� f (a) = 0.
�o�˪������ڭ̵����@�ӯS�����W�r.
Definition 9.4.4
���]
F �O�@�� field �B
L �O
F ���@�� extension field. ���]
a  L
L, �p�G�s�b
F[
x] �����@�ӫD 0 �� polynomial
f (
x) ����
f (
a) = 0, �h��
a �O
algebraic over
F.
�ҥH Theorem 9.3.7 �i�D�ڭ̥H�U���G:
Lemma 9.4.5
���]
F �O�@�� field �B
L �O
F ���@�� finite extension, �h
L
�����������O algebraic over
F.
���@�� extensional field of F �����������O algebraic over F ��,
�ڭ̺ٳo�� extension �O�@�� algebraic extension. Lemma
9.4.5 �i�D�ڭ̥��� finite extension of F �]���O algebraic
extension of F. ���L�n�`�N���O�@�� algebraic extension of F
���@�w�O finite extension of F.
�̫�ڭ̦A�ݤ@�Ӧ��� finite extension ���n���ʽ�. �p�G F �O�@��
field, K �O F �� �@�� extension field, �ӤS L �O K ���@��
extension field. �]�N�O�ڭ̦�
F  K
K  L �o�@�����Y.
���M�F L �]�i�ݦ��O F ���@�� extension. ��Y���] K over F �M
L over K ���O finite extension, �ڭ̦۵M�|�ݨ��� L �ݦ��O F
�� extension �ɬO�_�]�O finite extension?
L �o�@�����Y.
���M�F L �]�i�ݦ��O F ���@�� extension. ��Y���] K over F �M
L over K ���O finite extension, �ڭ̦۵M�|�ݨ��� L �ݦ��O F
�� extension �ɬO�_�]�O finite extension?
Theorem 9.4.6
���]
F �O�@�� field,
L �M
K ���O
F �� extensions �B�ŦX
F  K
K  L
L. �Y�w��
K �O
F ���@�� finite extension
�B
L �O
K ���@�� finite extension, �h
L �]�O
F ���@�� finite
extension, �ӥB
[L : F] = [L : K][K : F].
�� ��.
���] [
K :
F] =
m �H�� [
L :
K] =
n, �ڭ̷Q�ҩ�
L �O�@�� finite
extension of
F �B�� degree ��
m . n. �� [
K :
F] =
m �����]��
dim
F(
K) =
m, �Y�s�b
a1,...,
am  K
K �O
K over
F ���@��
basis. �P�˪��s�b
b1,...,
bn  L
L �O
L over
K ���@�� basis.
�ڭ̷Q�ҩ�
{
ai . bj},

�O
L over
F ���@�� basis. �p���۵M�o�ҥ��w�z.
�����n�`�N���O�]��
K  L
L �ҥH��
ai  K
K,
bj  L
L
�۵M�i�o
ai . bj  L
L. �ڭ̭n�ҩ��o��
ai . bj span
L
over
F �B�O linearly independent over
F.
�����ҩ�
{ai . bj} span L over F: ����

 L,
�ڭ̭n���
ci, j
L,
�ڭ̭n���
ci, j  F �ϱo
F �ϱo
�M�Ӧ]
b1,...,
bn span
L over
K, �ڭ̥i�H���
d1,...,
dn  K
K
�ϱo
 = d1 . b1 + ... + dn . bn. = d1 . b1 + ... + dn . bn. |
(9.4) |
�A�Q��
a1,...,
am span
K over
F, ����@
dj  K
K, �ڭ̳��i�H���
c1, j,...,
cm, j  F
F �ϱo
dj = c1, j . a1 + c2, j . a2 + ... + cm, j . am.
�N�o��
dj �a�J���l (
9.4), �o��
{
ai . bj} span
L
over
F.
�����ҩ�
{ai . bj} �O linearly independent over F.
�Q�Τ��Ҫk, ���]�s�b�@�դ����� 0 ��
ci, j  F �ϱo
F �ϱo
 ci, j . (ai . bj) = 0. �o����
ci, j . (ai . bj) = 0. �o����
| 0 |
= |
(c1, 1 . a1 + c2, 1 . a2 + ... + cm, 1 . am) . b1 |
|
| |
|
+ ... + (c1, n . a1 + c2, n . a2 + ... + cm, n . am) . bn |
|
�`�N����N��
j = 1,...,
n, �Y�O
dj = c1, j . a1 + c2, j . a2 + ... + cm, j . am,
�]��
ci, j  F
F,
ai  K
K �B
F  K
K, �ڭ̦�
dj  K
K �B
0 = d1 . b1 + d2 . b2 + ... + dn . bn.
�]��
b1,...,
bn �O
linearly independent over
K, �G�o
d1 =
d2 =
... =
dn = 0.
���y�ܻ�����N��
j = 1,...,
n, �Ҧ�
0 = dj = c1, j . a1 + c2, j . a2 + ... + cm, j . am.
�A�Q��
a1,...,
am �O linearly independent over
F �H�γo��
ci, j
���ݩ�
F, �ڭ̱o�o��
ci, j �ҵ��� 0. ���M���찲�]
ci, j
������ 0 �ۥ٬�, �G�o��
{
ai . bj} �O linearly independent
over
F.

�n�`�N Theorem 9.4.6 ��������O�n�D K �O F �� finite
extension �B L �O K �� finite extension � ����o L �O F ��
finite extension. �ڭ̦۵M�|�ݤϹL�ӹ��? �]�N�O�����p�G�w��
L �O F �� finite extension, �ڭ̬O�_�i�o K �O F �� finite
extension �B L �O K �� finite extension �O? ���O�֩w��,
�ƹ�W�ڭ̦��H�U�����G:
Corollary 9.4.7
���]
F �O�@�� field,
L �M
K ���O
F �� extensions �B�ŦX
F  K
K  L
L. �Y�w��
L �O
F ���@�� finite
extension, �h
K �O
F ���@�� finite extension �B
L �O
K
���@�� finite extension, �ӥB
[L : F] = [L : K][K : F].
�� ��.
��
F  K
K  L
L �o�����Y��, �ڭ̥i�N
K �ݦ��O
L
over
F �� subspace, �ҥH�� Lemma
9.3.4 (3) ��
dim
F(
L)

dim
F(
K), ���y�ܻ��Y
L over
F �O�@�� finite
extension ����
K over
F ���M�]�O finite extension.
�t�@�譱�Y���]
[
L :
F] = dim
F(
L) =
n, �]�N���s�b
a1,...,
an  L
L
�O�@��
L over
F �� basis, �ѩ�
a1,...,
an span
L over
F
�A�[�W
F  K
K, �ڭ̷��M��
a1,...,
an �] span
L over
K. �ҥH�Q�� Lemma
9.3.4 (1) ��
dim
K(
L)
 n
n = dim
F(
L).
�]���o
L �O
K ���@�� finite extension.
�W���w�ҭY L �O F ���@�� finite extension, �h K �O F ���@��
finite extension �B L �O K ���@�� finite extension. �]���i�M��
Theorem 9.4.6 �o��
[L : F] = [L : K][K : F].




�U�@��: ���� Field ���ʽ�
�W�@��: ��� Field ���ʽ�
�e�@��: �N ring �ݦ��O vector
Administrator
2005-06-18
![]() dimF(L), ���y�ܻ� R �O�@�� finite dimensional
vector space over F. �]���Q�� Theorem 9.3.7 (2) �o�� R
�O�@�� field.
dimF(L), ���y�ܻ� R �O�@�� finite dimensional
vector space over F. �]���Q�� Theorem 9.3.7 (2) �o�� R
�O�@�� field.
![]()
![]() L
�Ҧs�b�@�� F[x] ���� polynomial f (x)
L
�Ҧs�b�@�� F[x] ���� polynomial f (x)![]() 0 ���� f (a) = 0.
�o�˪������ڭ̵����@�ӯS�����W�r.
0 ���� f (a) = 0.
�o�˪������ڭ̵����@�ӯS�����W�r.
![]() K
K ![]() L �o�@�����Y.
���M�F L �]�i�ݦ��O F ���@�� extension. ��Y���] K over F �M
L over K ���O finite extension, �ڭ̦۵M�|�ݨ��� L �ݦ��O F
�� extension �ɬO�_�]�O finite extension?
L �o�@�����Y.
���M�F L �]�i�ݦ��O F ���@�� extension. ��Y���] K over F �M
L over K ���O finite extension, �ڭ̦۵M�|�ݨ��� L �ݦ��O F
�� extension �ɬO�_�]�O finite extension?
![]()
![]() L,
�ڭ̭n���
ci, j
L,
�ڭ̭n���
ci, j ![]() F �ϱo
F �ϱo
![]() F �ϱo
F �ϱo
![]() ci, j . (ai . bj) = 0. �o����
ci, j . (ai . bj) = 0. �o����