

下一頁: Field 的 Characteristic
上一頁: 初級 Field 的性質
前一頁: 初級 Field 的性質
這一節中我們首先介紹一些直接由定義得到的 field 的性質.
回顧一下一個 field 是一個 commutative ring with 1 而且其中非 0
的元素都是 unit. 也就是若 F 是一個 field, 則 F 中的 + 和
. 需滿足 Definition 5.1.1 中 (R1) 到 (R8) 的性質,
另?nbsp;需有:
- 對任意 a, b
 F 皆滿足
a . b = b . a.
F 皆滿足
a . b = b . a.
- 存在 1
 F 使得對任意 a
F 使得對任意 a  F 皆滿足
a . 1 = 1 . a = a.
F 皆滿足
a . 1 = 1 . a = a.
- 對任意 a
 F 且 a
F 且 a 0, 皆存在
a-1
0, 皆存在
a-1  F 使得
a . a-1 = a-1 . a = 1.
F 使得
a . a-1 = a-1 . a = 1.
前兩項是要求 F 是一個 commutative ring with 1; 最後一項是要求
F 中不為 0 的元素都是 unit.
很快的利用以上的定義我們可以得到以下有關 field 簡單但重要的性質.
証 明.
由 field 的定義已知
F 是一個 commutative ring with 1,
所以我們只要證明
F 中沒有 zero-divisor 即可. 這可有由 Lemma
5.3.7 馬上得知, 不過為了完整性我們再給一次證明.
若 a  F 是 F 中的一個 zero-divisor, 即 a
F 是 F 中的一個 zero-divisor, 即 a 0 且存在 b
0 且存在 b 0 滿足
a . b = 0. 然而由 b
0 滿足
a . b = 0. 然而由 b 0 知 b 是 F 中的 unit,
故知存在
b-1
0 知 b 是 F 中的 unit,
故知存在
b-1  F 滿足
b . b-1 = 1. 因此可得
F 滿足
b . b-1 = 1. 因此可得
0 = (a . b) . b-1 = a . (b . b-1) = a . 1 = a.
此和
a
0
的假設相矛盾, 故
a 不可能是
F 中的 zero-divisor.

以後我們會看到 Lemma 9.1.1 在有關 field
的性質的推導過竣井雃h地方占了關鍵性的地位. 首先看一個簡單的例子:
Corollary 9.1.2
假設
F 是一個 field, 令
F* =
F 
{0} 表示
F 中不為 0
的元素所成的集合, 則
F* 在乘法的運算之下是一個 abelian group.
証 明.
利用
F 是一個 ring with 1, 我們知道
F* 滿足 Definition
1.1.1 中 (GP2) 和 (GP3) 的條件. 再來若
a  F*
F* 我們知存在
a-1  F
F 滿足
a . a-1 = 1, 然而
a-1 不可能是 0,
否則會造成
a . a-1 =
a . 0 = 0. 故知
a-1  F*
F*,
也就是說
F* 也滿足 Definition
1.1.1 中 (GP4) 的性質.
因此要證明
F* 在乘法的運算之下是一個 group 我們僅要檢查 (GP1).
也就是說若
a,
b  F*
F*, 則
a . b  F*
F*. 然而
a,
b  F*
F*
表示
a,
b  F
F 且
a
0,
b
0, 故由 Lemma
9.1.1 知
a . b
0, 即
a . b  F*
F*. 至於
F* 是 abelian, 則由
F 是 commutative ring 馬上得知.

Example 9.1.3
考?
這一個
ring. 由於 5 是

中的 irreducible element 且

是
principle ideal domain 利用 Lemma
8.3.2 知
5

=
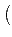
5
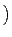
是

中的 maximal ideal. 所以知

/5

是一個 field (Theorem
6.5.11). 我們可以驗證
在乘法之下是一個
abelian group. 事實上由
可知
(

/5

)
* 在乘法之下是一個 cyclic group (因
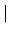
(

/5

)
*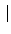
= 4 且
ord(
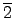
) = 4).
假設 F 是一個 field 且
S  F. 如果將 F
的加法與乘法運算限制在 S 中來看, S 也是一個 field, 則稱 S 是
F 的 subfield. 因此如果 S 在 F 的加法之下是 F 的
subgroup 且
S* = S
F. 如果將 F
的加法與乘法運算限制在 S 中來看, S 也是一個 field, 則稱 S 是
F 的 subfield. 因此如果 S 在 F 的加法之下是 F 的
subgroup 且
S* = S  {0} 在 F* 的乘法之下是 F* 的
subgroup, 則 S 就會是 F 的 subfield. 因此利用 Lemma 1.3.4
我們有以下的檢查 subfield 的方法.
{0} 在 F* 的乘法之下是 F* 的
subgroup, 則 S 就會是 F 的 subfield. 因此利用 Lemma 1.3.4
我們有以下的檢查 subfield 的方法.
Lemma 9.1.4
假設
F 是一個 field 且
S  F
F. 如果對任意
a,
b  S
S, 其中
b
0 皆有
a -
b  S
S 且
a . b-1  S
S, 則
S 是
F 的
subfield.
接下來我們來看 field 之間 homomorphism 的性質. 若 R 和 R' 是兩個
ring 且
 : R
: R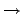 R', 其中對任意的 a
R', 其中對任意的 a  R 皆有
R 皆有  (a) = 0,
則依定義
(a) = 0,
則依定義  當然是 R 到 R' 的一個 ring homomorphism.
不過這種 ring homomorphism 對我們來說是無用的, 一般我們稱之為 trivial homomorphism.
當然是 R 到 R' 的一個 ring homomorphism.
不過這種 ring homomorphism 對我們來說是無用的, 一般我們稱之為 trivial homomorphism.
Proposition 9.1.5
假設
F 和
F' 都是 field 且 1
F 和 1
F' 分別是
F 和
F'
中乘法的 identity. 如果

:
F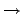 F'
F' 是一個 nontrivial 的 ring
homomorphism, 則
-
 (1F) = 1F'.
(1F) = 1F'.
 是一對一的 homomorphism.
是一對一的 homomorphism.
証 明.
(1) 我們要證明

(1
F) 是
F' 的乘法 identity. 由於

不是
trivial, 故存在
a  F
F 使得

(
a)

0. 然而

(
a) =

(
a . 1
F), 利用

是 ring homomorphism 我們得

(
a) =

(
a)
. 
(1
F). 然而在
F' 中我們仍然有

(
a)
. 1
F' =

(
a), 故得

(
a)
. 
(1
F) =

(
a)
. 1
F', 也就是說
利用
F' 是一個 integral domain
(Lemma
9.1.1) 且

(
a)

0, 我們得證

(1
F) = 1
F'.
(2) 要證明  是一對一的等價於要證明
ker(
是一對一的等價於要證明
ker( ) =
) = 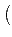 0
0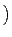 (Lemma
6.3.4). 然而因
ker(
(Lemma
6.3.4). 然而因
ker( ) 一定是 F 的一個 ideal (Lemma
6.3.3) 且 F 中僅有 F 和
) 一定是 F 的一個 ideal (Lemma
6.3.3) 且 F 中僅有 F 和
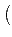 0
0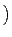 這兩個 trivial ideals
(Lemma 6.2.4) 所以可知
ker(
這兩個 trivial ideals
(Lemma 6.2.4) 所以可知
ker( ) = F 或
ker(
) = F 或
ker( ) =
) = 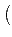 0
0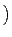 . 但如果
ker(
. 但如果
ker( ) = F, 表示對任意 a
) = F, 表示對任意 a  F
皆使得
F
皆使得  (a) = 0, 此與
(a) = 0, 此與  不是 trivial 的 ring homomorphism
相矛盾. 故知
ker(
不是 trivial 的 ring homomorphism
相矛盾. 故知
ker( ) =
) = 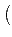 0
0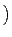 , 也就是說
, 也就是說  是一對一的 ring
homomorphism.
是一對一的 ring
homomorphism.



下一頁: Field 的 Characteristic
上一頁: 初級 Field 的性質
前一頁: 初級 Field 的性質
Administrator
2005-06-18
![]() F 是 F 中的一個 zero-divisor, 即 a
F 是 F 中的一個 zero-divisor, 即 a![]() 0 且存在 b
0 且存在 b![]() 0 滿足
a . b = 0. 然而由 b
0 滿足
a . b = 0. 然而由 b![]() 0 知 b 是 F 中的 unit,
故知存在
b-1
0 知 b 是 F 中的 unit,
故知存在
b-1 ![]() F 滿足
b . b-1 = 1. 因此可得
F 滿足
b . b-1 = 1. 因此可得
![]() F. 如果將 F
的加法與乘法運算限制在 S 中來看, S 也是一個 field, 則稱 S 是
F 的 subfield. 因此如果 S 在 F 的加法之下是 F 的
subgroup 且
S* = S
F. 如果將 F
的加法與乘法運算限制在 S 中來看, S 也是一個 field, 則稱 S 是
F 的 subfield. 因此如果 S 在 F 的加法之下是 F 的
subgroup 且
S* = S ![]() {0} 在 F* 的乘法之下是 F* 的
subgroup, 則 S 就會是 F 的 subfield. 因此利用 Lemma 1.3.4
我們有以下的檢查 subfield 的方法.
{0} 在 F* 的乘法之下是 F* 的
subgroup, 則 S 就會是 F 的 subfield. 因此利用 Lemma 1.3.4
我們有以下的檢查 subfield 的方法.
![]() : R
: R![]() R', 其中對任意的 a
R', 其中對任意的 a ![]() R 皆有
R 皆有 ![]() (a) = 0,
則依定義
(a) = 0,
則依定義 ![]() 當然是 R 到 R' 的一個 ring homomorphism.
不過這種 ring homomorphism 對我們來說是無用的, 一般我們稱之為 trivial homomorphism.
當然是 R 到 R' 的一個 ring homomorphism.
不過這種 ring homomorphism 對我們來說是無用的, 一般我們稱之為 trivial homomorphism.
![]() 是一對一的等價於要證明
ker(
是一對一的等價於要證明
ker(![]() ) =
) = ![]() 0
0![]() (Lemma
6.3.4). 然而因
ker(
(Lemma
6.3.4). 然而因
ker(![]() ) 一定是 F 的一個 ideal (Lemma
6.3.3) 且 F 中僅有 F 和
) 一定是 F 的一個 ideal (Lemma
6.3.3) 且 F 中僅有 F 和
![]() 0
0![]() 這兩個 trivial ideals
(Lemma 6.2.4) 所以可知
ker(
這兩個 trivial ideals
(Lemma 6.2.4) 所以可知
ker(![]() ) = F 或
ker(
) = F 或
ker(![]() ) =
) = ![]() 0
0![]() . 但如果
ker(
. 但如果
ker(![]() ) = F, 表示對任意 a
) = F, 表示對任意 a ![]() F
皆使得
F
皆使得 ![]() (a) = 0, 此與
(a) = 0, 此與 ![]() 不是 trivial 的 ring homomorphism
相矛盾. 故知
ker(
不是 trivial 的 ring homomorphism
相矛盾. 故知
ker(![]() ) =
) = ![]() 0
0![]() , 也就是說
, 也就是說 ![]() 是一對一的 ring
homomorphism.
是一對一的 ring
homomorphism.
![]()