


§U§@≠∂: Unique Factorization Domain
§W§@≠∂: Integral Domain §W™ļ§ņł—© ĹŤ
ęe§@≠∂: Euclidean Domain
≥o§@ł`§§ßŕ≠ŐĪNĪīįQ principle ideal domain ™ļįÚ•Ľ© ĹŤ. •—©ů§w™ĺ§@≠”
Euclidean domain §@©w¨O principle ideal domain,
©“•H≥o§@ł`©“ĹÕ™ļ© ĹŤ∑ŪĶMĺA•ő©ů Euclidean Domain.
ęe≠Īī£ĻLĻÔ§@ĮŽ™ļ integral domain •ŰĶĻ®‚≠”ęD 0 §łĮņ®š greatest
common divisor §£§@©w¶s¶b. §£ĻLĻÔ©ů principle ideal domain,
•Ű∑N®‚≠”ęD 0 §łĮņ§ß greatest common divisor īN§@©w¶s¶b§F!
Proposition 8.3.1
į≤≥]
R ¨O§@≠” principle ideal domain. ĻÔ•Ű∑N
a,
b  R
R •B
a,
b
0 ®š greatest common divisor ¶s¶b. ¶”•B, ≠Y
d ¨O
a,
b ™ļ§@≠”
greatest common divisor, ęh¶s¶b
r,
s  R
R ®ŌĪo
d =
r . a +
s . b.
Ķż ©ķ.
≠ļ•ż¶“ľ
 a
a
+
 b
b
≥o§@≠” ideal. •—©ů
R ¨O principle ideal
domain, ¨G¶s¶b
d  R
R ļ°®¨
 d
d
=
 a
a
+
 b
b
. ßŕ≠Ő∑Q≠n√“©ķ
d īN¨O
a,
b ™ļ greatest common divisor.
≠ļ•ż•ż√“©ķ d ¨O a, b ™ļ common divisor. •—©ů
¨G•— Lemma
8.1.2 ™ĺ
d |
a. ¶P≤z•i√“
d |
b, ¨GĪo
d ¨O
a,
b
™ļ§@≠” common divisor.
ĪĶ§U®”√“©ķ≠Y c ¨O a, b ™ļ§@≠” common divisor, ęh c | d.
ĶM¶”≠Y c | a •B c | b, ™Ū•‹
 a
a

 c
c •B
•B
 b
b

 c
c . •—©ů
. •—©ů
 c
c ¨O§@≠” ideal,
•¶¶≥•[™k™ļę ≥¨© , ¨GĪo
¨O§@≠” ideal,
•¶¶≥•[™k™ļę ≥¨© , ¨GĪo
 a
a +
+  b
b

 c
c . §]īN¨OĽ°
. §]īN¨OĽ°
 d
d

 c
c . ¨GĪo√“ c | d.
. ¨GĪo√“ c | d.
≥Őꊕ—©włq,
 a
a +
+  b
b §§™ļ§łĮņ≥£¨O
r . a + s . b, ®š§§
r, s
§§™ļ§łĮņ≥£¨O
r . a + s . b, ®š§§
r, s  R ≥oļōßő¶°. ¨G•—
d
R ≥oļōßő¶°. ¨G•—
d 
 d
d =
=  a
a +
+  b
b ™ĺ§@©w¶s¶b
r, s
™ĺ§@©w¶s¶b
r, s  R ®ŌĪo
d = r . a + s . b. ≥o≠”ĮS© ĻÔ©ů•Ű∑N a, b ™ļ
greatest common divisor ¨“ĻÔ. ≥o¨O¶]¨į•— Lemma 8.1.6 ™ĺ≠Y
d' ¨O a, b •t§@≠” greatest common divisor, ęhßŕ≠Ő®ŐĶM¶≥
R ®ŌĪo
d = r . a + s . b. ≥o≠”ĮS© ĻÔ©ů•Ű∑N a, b ™ļ
greatest common divisor ¨“ĻÔ. ≥o¨O¶]¨į•— Lemma 8.1.6 ™ĺ≠Y
d' ¨O a, b •t§@≠” greatest common divisor, ęhßŕ≠Ő®ŐĶM¶≥
 d'
d' =
=  d
d =
=  a
a +
+  b
b .
.

``≠Y d ¨O a, b ™ļ§@≠” greatest common divisor, ęh¶s¶b r, s  R
ļ°®¨
d = r . a + s . r'' ≥o§@≠”ĮS© ęDĪ`¶≥•ő.
§jģa•i•HßQ•ő≥o≠”ĮS© ¶A•ť∑” Proposition 7.1.7 ©ő Proposition
7.2.11 ™ļĶż©ķ§Ť¶°√“Īo§@≠” principle ideal domain §§™ļ
irreducible element ≥£¨O prime element. §£ĻL≥ołŐßŕ≠Ő§∂≤–•t§@ļōßQ•ő
ideal §Ť™k™ļ√“©ķ.
R
ļ°®¨
d = r . a + s . r'' ≥o§@≠”ĮS© ęDĪ`¶≥•ő.
§jģa•i•HßQ•ő≥o≠”ĮS© ¶A•ť∑” Proposition 7.1.7 ©ő Proposition
7.2.11 ™ļĶż©ķ§Ť¶°√“Īo§@≠” principle ideal domain §§™ļ
irreducible element ≥£¨O prime element. §£ĻL≥ołŐßŕ≠Ő§∂≤–•t§@ļōßQ•ő
ideal §Ť™k™ļ√“©ķ.
Lemma 8.3.2
į≤≥]
R ¨O§@≠” principle ideal domain,
a  R
R •B
a
0. ≠Y
a
¨O
R ™ļ§@≠” irreducible element ęh
 a
a
¨O
R ™ļ§@≠” maximal
ideal. §Ō§ß, ≠Y
 a
a
¨O
R ™ļ§@≠” maximal ideal, ęh
a ¨O
R
™ļ§@≠” irreducible element.
Ķż ©ķ.
¶p™G
a ¨O§@≠” irreducible element, •— Lemma
8.1.9 (1)
ßŕ≠Ő™ĺĻDßš§£®ž§@≠” nontrivial ™ļ principle ideal §∂©ů
 a
a
©M
R §ß∂°. §£ĻL•—
R ¨O principle ideal ™ļį≤≥]™ĺ
R §§™ļ ideal ≥£¨O
principle ideal. īę•ył‹Ľ°īN¨Oßš§£®ž§@≠” ideal §∂©ů
 a
a
©M
R
§ß∂°. ¨GĪo
 a
a
¨O§@≠” maximal ideal.
§Ō§ß, ¶p™G
 a
a ¨O§@≠” maximal ideal, ∑ŪĶMßš§£®ž nontrivial
principle ideal •]ßt
¨O§@≠” maximal ideal, ∑ŪĶMßš§£®ž nontrivial
principle ideal •]ßt
 a
a . ¨GßQ•ő Lemma 8.1.9 (1) ™ĺ
a ¨O§@≠” irreducible element.
. ¨GßQ•ő Lemma 8.1.9 (1) ™ĺ
a ¨O§@≠” irreducible element.

¶^ŇU§@§U Lemma 8.1.9 ™ļ•t§@≥°§ņ¨OĽ° a ¨O prime element
≠Y•BįŖ≠Y
 a
a ¨O§@≠” prime ideal.
©“•Hßŕ≠Őę‹ß÷™ļīN•i•HĪo®ž•H§U§ßĶ≤™G.
¨O§@≠” prime ideal.
©“•Hßŕ≠Őę‹ß÷™ļīN•i•HĪo®ž•H§U§ßĶ≤™G.
Proposition 8.3.3
į≤≥]
R ¨O§@≠” principle ideal domain, ęh
R §§™ļ irreducible
element ≥£¨O prime element. §Ō§ß,
R §§™ļ prime element ≥£¨O
irreducible element.
Ķż ©ķ.
¶]¨į
R ¨O integral domain, Lemma
8.1.8 ßi∂Dßŕ≠Ő
R §§™ļ
prime element ≥£¨O irreducible element.
§Ō§ß, ≠Y a ¨O R §§™ļ irreducible element, •— Lemma 8.3.2
™ĺ
 a
a ¨O R ™ļ§@≠” maximal ideal. ĶM¶” Corollary 6.5.13
ßi∂Dßŕ≠Ő R §§™ļ maximal ideal ≥£¨O prime ideal, ¨G™ĺ
¨O R ™ļ§@≠” maximal ideal. ĶM¶” Corollary 6.5.13
ßi∂Dßŕ≠Ő R §§™ļ maximal ideal ≥£¨O prime ideal, ¨G™ĺ
 a
a ¨O
R ™ļ§@≠” prime ideal. ¶]¶ĻßQ•ő Lemma 8.1.9 (2) Īo√“ a
¨O§@≠” prime element.
¨O
R ™ļ§@≠” prime ideal. ¶]¶ĻßQ•ő Lemma 8.1.9 (2) Īo√“ a
¨O§@≠” prime element.

ęe≠Īī£ĻL¶b§@ĮŽ™ļ commutative ring with 1 §§™ļ maximal ideal ≥£¨O
prime ideal, ¶ż¨O prime ideal •ľ•≤¨O maximal ideal. ĶM¶” Lemma
8.3.2 •H§ő Proposition 8.3.3 ĪN principle ideal
domain §§™ļ maximal ideal ©M prime ideal ĶĻ§F§@≠”≠ę≠n™ļ√Ų≥s.
Corollary 8.3.4
į≤≥]
R ¨O§@≠” principle ideal domain •B
I ¨O
R §§§@≠”ęD 0 ™ļ
ideal. ęh
I ¨O§@≠” prime ideal ≠Y•BįŖ≠Y
I ¨O§@≠” maximal ideal.
ßŕ≠ŐīŅłgßQ•ő
 ©M F[x] §§™ļ irreducible element ©M prime
element ¨O¨Ř¶P™ļ√“©ķ
©M F[x] §§™ļ irreducible element ©M prime
element ¨O¨Ř¶P™ļ√“©ķ
 ©M F[x] ™ļįŖ§@§ņł—© ĹŤ.
ßŕ≠Ő≤¶bīX•G§w®žĻF•i•H√“©ķ principle ideal domain
™ļįŖ§@§ņł—© ĹŤ™ļ•ōľ–. §£ĻL∑Ūģ…ßŕ≠Ő¶b
©M F[x] ™ļįŖ§@§ņł—© ĹŤ.
ßŕ≠Ő≤¶bīX•G§w®žĻF•i•H√“©ķ principle ideal domain
™ļįŖ§@§ņł—© ĹŤ™ļ•ōľ–. §£ĻL∑Ūģ…ßŕ≠Ő¶b
 ©M F[x]
§§¨OßQ•őľ∆嫬kĮ«™k®”√“©ķįŖ§@§ņł—© ĹŤ, ≤¶b¶b§@ĮŽ™ļ principle ideal
domain ßŕ≠Ő®SŅž™k®Ō•őľ∆嫬kĮ«™k. §U§@≠” Lemma
•i•HņįßUßŕ≠ŐßJ™A≥o≠”ßx√Ý.
©M F[x]
§§¨OßQ•őľ∆嫬kĮ«™k®”√“©ķįŖ§@§ņł—© ĹŤ, ≤¶b¶b§@ĮŽ™ļ principle ideal
domain ßŕ≠Ő®SŅž™k®Ō•őľ∆嫬kĮ«™k. §U§@≠” Lemma
•i•HņįßUßŕ≠ŐßJ™A≥o≠”ßx√Ý.
Lemma 8.3.5
į≤≥]
R ¨O§@≠” principle ideal domain, ęhĶL™k¶b
R
§§ßš®žĶLĹa¶h≠”ńYģśĽľľW™ļ ideals. īę•ył‹Ľ°¶p™G
{
In}
n = 1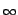
¨O§@≤’
R §§™ļ ideal ļ°®¨
ęh¶s¶b
m 

®ŌĪo
Im =
Im + 1 =
... .
Ķż ©ķ.
≠ļ•żßŕ≠Ő¶“ľ
I =
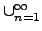 In
In ≥o§@≠”∂į¶X. ßŕ≠Ő∑Q≠n√“©ķ
I
¨O
R §§™ļ ideal. (≠n™`∑N§@ĮŽ®”ŃŅ≠Y
J1,
J2 ¨O
R ™ļ ideal ®ļĽÚ
J1 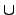 J2
J2 §£§@©w¨O
R ™ļ ideals. §£ĻL¶b≥ołŐ•—©ů
In
¶≥•]ßt™ļ√ŲęY, ßŕ≠Ő•i•H√“•X
I ¨O§@≠” ideal.)
į≤≥] a, b  I, īę•ył‹Ľ°¶s¶b
i, j
I, īę•ył‹Ľ°¶s¶b
i, j 
 ®ŌĪo a
®ŌĪo a  Ii •B b
Ii •B b  Ij. į≤≥] i
Ij. į≤≥] i j, •—į≤≥]™ĺ
Ij
j, •—į≤≥]™ĺ
Ij  Ii. ¨GĪo
a, b
Ii. ¨GĪo
a, b  Ii.
¶]¶Ļ•— Ii ¨O§@≠” ideal, ßŕ≠Ő¶≥
a - b
Ii.
¶]¶Ļ•— Ii ¨O§@≠” ideal, ßŕ≠Ő¶≥
a - b  Ii. ©“•HĪo a - b
Ii. ©“•HĪo a - b  I.
•t• ≠Y a
I.
•t• ≠Y a  I •B r
I •B r  R, •—į≤≥]™ĺ¶s¶b
i
R, •—į≤≥]™ĺ¶s¶b
i 
 ®ŌĪo a
®ŌĪo a  Ii.
¨GĪo
a . r
Ii.
¨GĪo
a . r  Ii, §]īN¨OĽ°
a . r
Ii, §]īN¨OĽ°
a . r  I. ¨G•— Lemma
6.1.2 ™ĺ I ¨O R §§™ļ§@≠” ideal.
I. ¨G•— Lemma
6.1.2 ™ĺ I ¨O R §§™ļ§@≠” ideal.
¨JĶM I ¨O R ™ļ ideal •B R ¨O principle ideal domain, ¨G¶s¶b
a  R ®ŌĪo
R ®ŌĪo
 a
a = I. ĶM¶”ßQ•ő
a
= I. ĶM¶”ßQ•ő
a 
 a
a = I ™ĺ¶s¶b
m
= I ™ĺ¶s¶b
m 
 ®ŌĪo a
®ŌĪo a  Im. ¨GßQ•ő
Im. ¨GßQ•ő
 a
a ¨O•]ßt a ≥Ő§p™ļ ideal
(Lemma 6.5.1) ™ĺ
I =
¨O•]ßt a ≥Ő§p™ļ ideal
(Lemma 6.5.1) ™ĺ
I =  a
a
 Im. īę•ył‹Ľ° I = Im,
¶]¶ĻßQ•őĻÔ©“¶≥™ļ i > m ¨“¶≥
Im
Im. īę•ył‹Ľ° I = Im,
¶]¶ĻßQ•őĻÔ©“¶≥™ļ i > m ¨“¶≥
Im  Ii •H§ő
Ii
Ii •H§ő
Ii  I
Īo√“ I = Im = Ii,
I
Īo√“ I = Im = Ii,
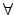 i > m.
i > m.

ßŕ≠Ő≠n¬«•ő Lemma 8.3.5 ™ļ•D≠n≠ž¶]¨O¶p™G d ¨O a ™ļ§@≠”
nontrivial divisor (ßY d | a ¶ż d §£¨O unit •B©M a §£
associates), ęh
 a
a
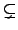
 d
d . ¶p¶Ļ§@®”, •i•H√“•X R
§§™ļ§łĮņ•uĮŗľg¶®¶≥≠≠¶h≠” irreducible element ™ļ≠ľŅn.
. ¶p¶Ļ§@®”, •i•H√“•X R
§§™ļ§łĮņ•uĮŗľg¶®¶≥≠≠¶h≠” irreducible element ™ļ≠ľŅn.
Theorem 8.3.6
į≤≥]
R ¨O§@≠” principle ideal domain •B
a ¨O
R §§§£¨į 0
•B§£¨O unit ™ļ§łĮņ, ęh
a •i•Hľg¶®¶≥≠≠¶h≠”
R §§™ļ irreducible
elements ™ļ≠ľŅn, ¶”•B≠Y©Ņ≤§ associates ™ļ√ŲęY•H§ő≠ľ™k™ļ∂∂ß«,
≥o≠”≠ľŅn™ļľg™kįŖ§@. §]īN¨OĽ°¶p™G
| a |
= |
p1n1 ... prnr |
|
| |
= |
q1m1 ... qsms |
|
®š§§
p1,...,
pr ¨O®‚®‚§£¨Ř associates ™ļ
irreducible elements •B
q1,...,
qs ¨O®‚®‚§£¨Ř associates ™ļ
irreducible elements, ęhłgĻLĺA∑Ū™ļŇ‹īę∂∂ß«, ßŕ≠Ő¶≥
r =
s,
pi  qi
qi •H§ő
ni =
mi,
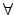 i
i = 1,...,
r.
Ķż ©ķ.
≠ļ•żßŕ≠Ő√“©ķ
a •i•Hľg¶®¶≥≠≠¶h≠” irreducible elements ™ļ≠ľŅn. ¶p™G
a §£Įŗľg¶®¶≥≠≠¶h≠” irreducible elements ™ļ≠ľŅn, ™Ū•‹
a •Ľ®≠§£¨O
irreducible, ¶]¶Ļ
a =
a1 . b1, ®š§§
a1,
b1  R
R ¨O
a ™ļ
nontrivial divisors •B
a1,
b1 §§•≤¶≥§@≠”§£Įŗľg¶®¶≥≠≠¶h≠”
irreducible elements ™ļ≠ľŅn. į≤≥]¨O
a1, ¶P§Wßŕ≠Ő™ĺ¶s¶b
a2,
b2  R
R ®ŌĪo
a1 =
a2 . b2, ®š§§
a2 ¨O
a1 ™ļ
nontrivial divisor •B
a2 §£Įŗľg¶®¶≥≠≠¶h≠” irreducible elements
™ļ≠ľŅn. ¶p¶Ļ§@™Ĺ§U•hßŕ≠ŐĽs≥y§F§@≥s¶Í™ļ ideals ≤ҶX
¶Ļ©M Lemma
8.3.5 •Ŕ¨ř, ¨G™ĺ
a §@©w•i•Hľg¶®¶≥≠≠¶h≠”
irreducible elements ™ļ≠ľŅn.
ĪĶ§U®”ßŕ≠Ő√“įŖ§@© . §@ĮŽ®”Ľ°≠Y§w√“Īo irreducible element īN¨O prime
element įŖ§@© īN¶Řį ¶®•Ŗ. ≥o¨O¶]¨į¶p™G
a = p1n1 ... prnr = q1m1 ... qsms,
•Ű®ķ
pi •—©ů
pi | q1m1 ... qsms,
•B
pi ¨O prime (Proposition
8.3.3) ™ĺ¶s¶b
j 
{1,...,
s} ®ŌĪo
pi |
qj. īꮕ§ß
pi ¨O
qj ™ļ§@≠” divisor. ĶM¶”
qj ¨O irreducible •B
pi
§£¨O unit, ¨GĪo
pi  qj
qj (ßY
pi ©M
qj associates).
¶]¶Ļßŕ≠Ő™ĺĻDĻÔ≥o≠”
pi, ¶b
{
q1,...,
qs} §§•uĮŗßš®žįŖ§@™ļ
qj ®ŌĪo
pi  qj
qj. ß_ęh≠Y
j j'
j' ¶ż
pi |
qj', ęh
¶P≤z•iĪo
pi  qj'
qj', ßQ•ő associates ¨O≠” equivalence relation
ßŕ≠ŐĪo
qj  qj'
qj', ≥o©Mį≤≥]≠Y
j j'
j' ęh§£•iĮŗ
qj  qj'
qj' ¨Ř•Ŕ¨ř. §Ō§ßĻÔ•Ű∑N™ļ
qj ßŕ≠Ő•i•H¶b
{
p1,...,
pr} §§ßš®žįŖ§@™ļ
pi ®ŌĪo
qj  pi
pi.
¶]¶Ļßŕ≠Ő¶b
{
p1,...,
pr} ©M
{
q1,...,
qs}
≥o®‚≠”∂į¶X§§ßš®ž§@ĻÔ§@™ļĻÔņ≥. §]īN¨OĽ°
r =
s •BłgĻLĺA∑Ū™ļ≠ęĪ∆ßŕ≠Ő¶≥
p1  q1
q1,...,
pr  qr
qr. ≤į≤≥]¨Y≠”
ni mi
mi,
¨į§F§ŤęKį_®£ßŕ≠ŐīNį≤≥]
n1 m1
m1 •B
n1 >
m1 ßa! •—©ů
q1 =
u . p1, ®š§§
u ¨O
R ™ļ§@≠” unit, ßŕ≠Ő¶≥
p1m1(p1n1 - m1 . p2n2 ... prnr - um1 . q2m2 ... qrmr) = 0.
ßQ•ő
p1m1
0 •B
R ¨O integral domain, ßŕ≠Ő¶≥
p1n1 - m1 . p2n2 ... prnr = um1 . q2m2 ... qrmr.
ĶM¶”•—©ů
n1 -
m1 > 0, •iĪo¶b
{
q2,...,
qr} §§¶s¶b
qj ®ŌĪo
p1 |
qj (™`∑N
u ¨O
unit ¨G§£•iĮŗ
p1 |
u). §]īN¨OĽ°
p1  qj
qj, ¶ż≥o©M
q1 ¨O
{
q1,...,
qr} §§įŖ§@ļ°®¨©M
p1 associates ™ļ§łĮņ¨Ř•Ŕ¨ř.
Īo√“•Ľ©w≤z.

ļ°®¨ Theorem 8.3.6 §§™ļįŖ§@§ņł—© ĹŤ™ļ ring ęDĪ`≠ę≠n,
ßŕ≠Ő§]ĶĻ•¶§@≠”ĮSģŪ™ļ¶W§l.
Definition 8.3.7
į≤≥] R ¨O§@≠” integral domain ¶”•B R §§ęD 0 •B§£¨O unit
™ļ§łĮņ≥£•i•Hľg¶®¶≥≠≠¶h≠” R §§™ļ irreducible elements ™ļ≠ľŅn,
¶”•B≠Y©Ņ≤§ associates ™ļ√ŲęY•H§ő≠ľ™k™ļ∂∂ß«, ≥o≠”≠ľŅn™ļľg™kįŖ§@, ęhļŔ
R ¨O§@≠” unique factorization domain.
Theorem 8.3.6 ßi∂Dßŕ≠Ő§@≠” principle ideal domain
§@©w¨O§@≠” unique factorization domain. ¶ż¨O§@≠” unique
factorization domain ®√§£§@©w¨O principle ideal domain. ßŕ≠ŐīŅłg®£ĻL
 [x] ¨O§@≠” unique factorization domain (Theorem 7.3.13)
¶ż®š§§
[x] ¨O§@≠” unique factorization domain (Theorem 7.3.13)
¶ż®š§§
 2
2 +
+  x
x ≥o§@≠” ideal ®√§£¨O principle ideal
(Example 7.3.1).
≥o§@≠” ideal ®√§£¨O principle ideal
(Example 7.3.1).



§U§@≠∂: Unique Factorization Domain
§W§@≠∂: Integral Domain §W™ļ§ņł—© ĹŤ
ęe§@≠∂: Euclidean Domain
Administrator
2005-06-18
![]() a
a![]()
![]()
![]() c
c![]() •B
•B
![]() b
b![]()
![]()
![]() c
c![]() . •—©ů
. •—©ů
![]() c
c![]() ¨O§@≠” ideal,
•¶¶≥•[™k™ļę ≥¨© , ¨GĪo
¨O§@≠” ideal,
•¶¶≥•[™k™ļę ≥¨© , ¨GĪo
![]() a
a![]() +
+ ![]() b
b![]()
![]()
![]() c
c![]() . §]īN¨OĽ°
. §]īN¨OĽ°
![]() d
d![]()
![]()
![]() c
c![]() . ¨GĪo√“ c | d.
. ¨GĪo√“ c | d.
![]() a
a![]() +
+ ![]() b
b![]() §§™ļ§łĮņ≥£¨O
r . a + s . b, ®š§§
r, s
§§™ļ§łĮņ≥£¨O
r . a + s . b, ®š§§
r, s ![]() R ≥oļōßő¶°. ¨G•—
d
R ≥oļōßő¶°. ¨G•—
d ![]()
![]() d
d![]() =
= ![]() a
a![]() +
+ ![]() b
b![]() ™ĺ§@©w¶s¶b
r, s
™ĺ§@©w¶s¶b
r, s ![]() R ®ŌĪo
d = r . a + s . b. ≥o≠”ĮS© ĻÔ©ů•Ű∑N a, b ™ļ
greatest common divisor ¨“ĻÔ. ≥o¨O¶]¨į•— Lemma 8.1.6 ™ĺ≠Y
d' ¨O a, b •t§@≠” greatest common divisor, ęhßŕ≠Ő®ŐĶM¶≥
R ®ŌĪo
d = r . a + s . b. ≥o≠”ĮS© ĻÔ©ů•Ű∑N a, b ™ļ
greatest common divisor ¨“ĻÔ. ≥o¨O¶]¨į•— Lemma 8.1.6 ™ĺ≠Y
d' ¨O a, b •t§@≠” greatest common divisor, ęhßŕ≠Ő®ŐĶM¶≥
![]() d'
d'![]() =
= ![]() d
d![]() =
= ![]() a
a![]() +
+ ![]() b
b![]() .
.
![]()
![]() R
ļ°®¨
d = r . a + s . r'' ≥o§@≠”ĮS© ęDĪ`¶≥•ő.
§jģa•i•HßQ•ő≥o≠”ĮS© ¶A•ť∑” Proposition 7.1.7 ©ő Proposition
7.2.11 ™ļĶż©ķ§Ť¶°√“Īo§@≠” principle ideal domain §§™ļ
irreducible element ≥£¨O prime element. §£ĻL≥ołŐßŕ≠Ő§∂≤–•t§@ļōßQ•ő
ideal §Ť™k™ļ√“©ķ.
R
ļ°®¨
d = r . a + s . r'' ≥o§@≠”ĮS© ęDĪ`¶≥•ő.
§jģa•i•HßQ•ő≥o≠”ĮS© ¶A•ť∑” Proposition 7.1.7 ©ő Proposition
7.2.11 ™ļĶż©ķ§Ť¶°√“Īo§@≠” principle ideal domain §§™ļ
irreducible element ≥£¨O prime element. §£ĻL≥ołŐßŕ≠Ő§∂≤–•t§@ļōßQ•ő
ideal §Ť™k™ļ√“©ķ.
![]() a
a![]() ¨O§@≠” maximal ideal, ∑ŪĶMßš§£®ž nontrivial
principle ideal •]ßt
¨O§@≠” maximal ideal, ∑ŪĶMßš§£®ž nontrivial
principle ideal •]ßt
![]() a
a![]() . ¨GßQ•ő Lemma 8.1.9 (1) ™ĺ
a ¨O§@≠” irreducible element.
. ¨GßQ•ő Lemma 8.1.9 (1) ™ĺ
a ¨O§@≠” irreducible element.
![]()
![]() a
a![]() ¨O§@≠” prime ideal.
©“•Hßŕ≠Őę‹ß÷™ļīN•i•HĪo®ž•H§U§ßĶ≤™G.
¨O§@≠” prime ideal.
©“•Hßŕ≠Őę‹ß÷™ļīN•i•HĪo®ž•H§U§ßĶ≤™G.
![]() a
a![]() ¨O R ™ļ§@≠” maximal ideal. ĶM¶” Corollary 6.5.13
ßi∂Dßŕ≠Ő R §§™ļ maximal ideal ≥£¨O prime ideal, ¨G™ĺ
¨O R ™ļ§@≠” maximal ideal. ĶM¶” Corollary 6.5.13
ßi∂Dßŕ≠Ő R §§™ļ maximal ideal ≥£¨O prime ideal, ¨G™ĺ
![]() a
a![]() ¨O
R ™ļ§@≠” prime ideal. ¶]¶ĻßQ•ő Lemma 8.1.9 (2) Īo√“ a
¨O§@≠” prime element.
¨O
R ™ļ§@≠” prime ideal. ¶]¶ĻßQ•ő Lemma 8.1.9 (2) Īo√“ a
¨O§@≠” prime element.
![]()
![]() 0 ®ŌĪo
I =
0 ®ŌĪo
I = ![]() a
a![]() . ¶p™G
. ¶p™G
![]() a
a![]() ¨O§@≠” prime ideal, ęh•— Lemma
8.1.9 ™ĺ a ¨O§@≠” prime element. ¨G•— Proposition
8.3.3 (©ő Lemma 8.1.8) ™ĺ a ¨O§@≠” irreducible
element. ¶]¶Ļ•— Lemma 8.3.2 ™ĺ
¨O§@≠” prime ideal, ęh•— Lemma
8.1.9 ™ĺ a ¨O§@≠” prime element. ¨G•— Proposition
8.3.3 (©ő Lemma 8.1.8) ™ĺ a ¨O§@≠” irreducible
element. ¶]¶Ļ•— Lemma 8.3.2 ™ĺ
![]() a
a![]() = I ¨O§@≠” maximal
ideal.
= I ¨O§@≠” maximal
ideal.
![]()
![]() ©M F[x] §§™ļ irreducible element ©M prime
element ¨O¨Ř¶P™ļ√“©ķ
©M F[x] §§™ļ irreducible element ©M prime
element ¨O¨Ř¶P™ļ√“©ķ
![]() ©M F[x] ™ļįŖ§@§ņł—© ĹŤ.
ßŕ≠Ő≤¶bīX•G§w®žĻF•i•H√“©ķ principle ideal domain
™ļįŖ§@§ņł—© ĹŤ™ļ•ōľ–. §£ĻL∑Ūģ…ßŕ≠Ő¶b
©M F[x] ™ļįŖ§@§ņł—© ĹŤ.
ßŕ≠Ő≤¶bīX•G§w®žĻF•i•H√“©ķ principle ideal domain
™ļįŖ§@§ņł—© ĹŤ™ļ•ōľ–. §£ĻL∑Ūģ…ßŕ≠Ő¶b
![]() ©M F[x]
§§¨OßQ•őľ∆嫬kĮ«™k®”√“©ķįŖ§@§ņł—© ĹŤ, ≤¶b¶b§@ĮŽ™ļ principle ideal
domain ßŕ≠Ő®SŅž™k®Ō•őľ∆嫬kĮ«™k. §U§@≠” Lemma
•i•HņįßUßŕ≠ŐßJ™A≥o≠”ßx√Ý.
©M F[x]
§§¨OßQ•őľ∆嫬kĮ«™k®”√“©ķįŖ§@§ņł—© ĹŤ, ≤¶b¶b§@ĮŽ™ļ principle ideal
domain ßŕ≠Ő®SŅž™k®Ō•őľ∆嫬kĮ«™k. §U§@≠” Lemma
•i•HņįßUßŕ≠ŐßJ™A≥o≠”ßx√Ý.
![]() I, īę•ył‹Ľ°¶s¶b
i, j
I, īę•ył‹Ľ°¶s¶b
i, j ![]()
![]() ®ŌĪo a
®ŌĪo a ![]() Ii •B b
Ii •B b ![]() Ij. į≤≥] i
Ij. į≤≥] i![]() j, •—į≤≥]™ĺ
Ij
j, •—į≤≥]™ĺ
Ij ![]() Ii. ¨GĪo
a, b
Ii. ¨GĪo
a, b ![]() Ii.
¶]¶Ļ•— Ii ¨O§@≠” ideal, ßŕ≠Ő¶≥
a - b
Ii.
¶]¶Ļ•— Ii ¨O§@≠” ideal, ßŕ≠Ő¶≥
a - b ![]() Ii. ©“•HĪo a - b
Ii. ©“•HĪo a - b ![]() I.
•t• ≠Y a
I.
•t• ≠Y a ![]() I •B r
I •B r ![]() R, •—į≤≥]™ĺ¶s¶b
i
R, •—į≤≥]™ĺ¶s¶b
i ![]()
![]() ®ŌĪo a
®ŌĪo a ![]() Ii.
¨GĪo
a . r
Ii.
¨GĪo
a . r ![]() Ii, §]īN¨OĽ°
a . r
Ii, §]īN¨OĽ°
a . r ![]() I. ¨G•— Lemma
6.1.2 ™ĺ I ¨O R §§™ļ§@≠” ideal.
I. ¨G•— Lemma
6.1.2 ™ĺ I ¨O R §§™ļ§@≠” ideal.
![]() R ®ŌĪo
R ®ŌĪo
![]() a
a![]() = I. ĶM¶”ßQ•ő
a
= I. ĶM¶”ßQ•ő
a ![]()
![]() a
a![]() = I ™ĺ¶s¶b
m
= I ™ĺ¶s¶b
m ![]()
![]() ®ŌĪo a
®ŌĪo a ![]() Im. ¨GßQ•ő
Im. ¨GßQ•ő
![]() a
a![]() ¨O•]ßt a ≥Ő§p™ļ ideal
(Lemma 6.5.1) ™ĺ
I =
¨O•]ßt a ≥Ő§p™ļ ideal
(Lemma 6.5.1) ™ĺ
I = ![]() a
a![]()
![]() Im. īę•ył‹Ľ° I = Im,
¶]¶ĻßQ•őĻÔ©“¶≥™ļ i > m ¨“¶≥
Im
Im. īę•ył‹Ľ° I = Im,
¶]¶ĻßQ•őĻÔ©“¶≥™ļ i > m ¨“¶≥
Im ![]() Ii •H§ő
Ii
Ii •H§ő
Ii ![]() I
Īo√“ I = Im = Ii,
I
Īo√“ I = Im = Ii,
![]() i > m.
i > m.
![]()
![]() a
a![]()
![]()
![]() d
d![]() . ¶p¶Ļ§@®”, •i•H√“•X R
§§™ļ§łĮņ•uĮŗľg¶®¶≥≠≠¶h≠” irreducible element ™ļ≠ľŅn.
. ¶p¶Ļ§@®”, •i•H√“•X R
§§™ļ§łĮņ•uĮŗľg¶®¶≥≠≠¶h≠” irreducible element ™ļ≠ľŅn.
![]() [x] ¨O§@≠” unique factorization domain (Theorem 7.3.13)
¶ż®š§§
[x] ¨O§@≠” unique factorization domain (Theorem 7.3.13)
¶ż®š§§
![]() 2
2![]() +
+ ![]() x
x![]() ≥o§@≠” ideal ®√§£¨O principle ideal
(Example 7.3.1).
≥o§@≠” ideal ®√§£¨O principle ideal
(Example 7.3.1).