Maximal ideals

注意, 別被 ``maximal'' 這個字給騙了. 在數學上很多情況下, maximal 是表示沒有東西比它大, 並不表示它比所有的東西大. (我們不這樣定主要是在很多情況下我們要探討的東西並不是 well-ordered, 也就是有時兩樣東西是不能比較的.) 因此, 若 M 是 R 的一個 maximal ideal 且 I 是 R 的一個 nontrivial proper ideal, 這並不表示 I $\subseteq$ M, 而只是說如果 M $\subseteq$ I, 則 I = M. 從這個看法大家應也可以看出有可能在 R 中有不只一個 maximal ideal. 希望下一個例子可以釐清這個觀念.

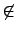
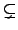
Example 6.5.10 考� $\mathbb {Z}$ 中 $\bigl($ 6 $\bigr)$ 這一個 ideal. 我們很容易看出來 $\bigl($ 6 $\bigr)$ $\subseteq$ $\bigl($ 2 $\bigr)$ 且因 2 $\in$ $\bigl($ 2 $\bigr)$ 但 2 $\not\in$ $\bigl($ 6 $\bigr)$ , 我們知 $\bigl($ 6 $\bigr)$ $\subsetneq$ $\bigl($ 2 $\bigr)$ . 再加上 $\bigl($ 2 $\bigr)$ 是 $\mathbb {Z}$ 的一個 nontrivial proper ideal, 故知 $\bigl($ 6 $\bigr)$ 不是 $\mathbb {Z}$ 的 maximal ideal. 不過 $\bigl($ 2 $\bigr)$ 是 $\mathbb {Z}$ 的 maximal ideal. 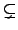因為如果 $\bigl($ 2 $\bigr)$ 不是 maximal ideal, 則依定義知存在一個 $\mathbb {Z}$ 中的 nontrivial proper ideal I 滿足 $\bigl($ 2 $\bigr)$ $\subsetneq$ I. 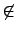換句說存在一整數 a $\in$ I 但 a $\not\in$ $\bigl($ 2 $\bigr)$ (這表示 a 是一個奇數). 所以存在一整數 n 使得 a = 2^.n + 1. 別忘了我們假設 I 是 ideal 且 2 $\in$ I, 所以 2^.n $\in$ I. 再加上 a $\in$ I, 因此得 1 = a - 2^.n $\in$ I. 由 Lemma 6.2.4 知 I = $\mathbb {Z}$ , 這和我們假設 I 是 nontrivial proper ideal 相矛盾, 故得 $\bigl($ 2 $\bigr)$ 是 $\mathbb {Z}$ 的 maximal ideal. 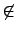不過由於 3 $\not\in$ $\bigl($ 2 $\bigr)$ , 我們知 $\bigl($ 3 $\bigr)$ 這個 ideal 並不包含於 $\bigl($ 2 $\bigr)$ . 甚至對任意的 n $\in$ $\mathbb {N}$ , $\bigl($ 3ⁿ $\bigr)$ 都不會包含於 $\bigl($ 2 $\bigr)$ . 所以 maximal ideal 會比所有的 nontrivial proper ideal 都大這樣的說法並不正確. 另一方面, 我們可以用前面類似的方法得到在 $\mathbb {Z}$ 中任意一個質數所產生的 principle ideal 都是 maximal ideal, 所以 $\mathbb {Z}$ 中的 maximal ideal 並不只一個 (其實有無窮多個).

接下來我們想用類似 Theorem 6.5.7 的方法利用 quotient ring 來判別一個 ideal 是否為 maximal ideal.

証明. 首先觀察由假設可知 R/M 是一個 commutative ring with 1, 所以 R/M 是一個 field 相當於只要說 R/M 中不等於 $\overline{0}$ 的元素都是 unit.

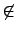盒眾] M 是 R 的 maximal ideal. 任取 R/M 中一元素 $\overline{a}$ $\ne$ $\overline{0}$ , 我們有 a $\in$ R 且 a $\not\in$ M. 由 Lemma 6.2.1 知

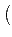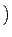
M + $\displaystyle \bigl($ a $\displaystyle \bigr)$ = {m + r^.a | m $\displaystyle \in$ M, r $\displaystyle \in$ R}

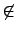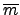
是 R 的一個 ideal. 由於 M $\subseteq$ M + $\bigl($ a $\bigr)$ 且 a $\not\in$ M, 我們知 M $\ne$ M + $\bigl($ a $\bigr)$ , 即 M + $\bigl($ a $\bigr)$ 是一個比 M 大的 ideal. 但由 M 是 maximal ideal 的假設我們知 M + $\bigl($ a $\bigr)$ 不是 R 的 nontrivial proper ideal. 換句話說 M + $\bigl($ a $\bigr)$ = R. 利用 1 $\in$ R = M + $\bigl($ a $\bigr)$ , 我們知存在 m $\in$ M, r $\in$ R 滿足 1 = m + r^.a. 別忘了我們是要討論 R/M 的元素, 所以由上式以及在 R/M 中 $\overline{m}$ = $\overline{0}$ 我們有

$\displaystyle \overline{1}$ = $\displaystyle \overline{m}$ + $\displaystyle \overline{r\cdot a}$ = $\displaystyle \overline{r}$ ^. $\displaystyle \overline{a}$ .

因此 $\overline{a}$ 是 R/M 的 unit, 故知 R/M 是一個 field.

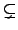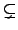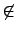反之若 R/M 是一個 field, 我們想證 M 是 R 的一個 maximal ideal. 再次強調我們不是要證明任意 R 中的 nontrivial proper ideal 都滿足 I $\subseteq$ M, 而是要證明不可能 M $\subsetneq$ I. 我們要用反證法: 假設 M 不是 maximal ideal, 即存在一個 nontrivial proper ideal I 滿足 M $\subsetneq$ I. 由 M $\subseteq$ I 但 M $\ne$ I 知存在 a $\in$ I 但 a $\not\in$ M, 也就是說在 R/M 中 $\overline{a}$ $\ne$ $\overline{0}$ . 但 R/M 是一個 field, 故存在 r $\in$ R 使得

$\displaystyle \overline{r}$ ^. $\displaystyle \overline{a}$ = $\displaystyle \overline{r\cdot a}$ = $\displaystyle \overline{1}$ .

這告訴我們 1 - r^.a $\in$ M, 也就是說 1 = m + r^.a 其中 m $\in$ M. 由於 a $\in$ I 且 I 是一個 ideal, 我們知 r^.a $\in$ I. 因此由 m $\in$ M $\subseteq$ I 得 1 = m + r^.a $\in$ I. Lemma 6.2.4 告訴我們 1 $\in$ I 表示 I = R, 此和 I 是 nontrivial proper ideal 相矛盾, 故知 M 是 maximal ideal. $\qedsymbol$

Remark 6.5.12 我們可以利用 Correspondence 定理很快的證明 Theorem 6.5.11. 回顧一下 Corollary 6.3.7 告訴我們 R/M 中的 ideal 都是由介於 R 和 M 間的 ideal 所形成. 因此若 M 是 maximal ideal, 表示介於 R 和 M 間所有的 ideal 只有 R 和 M. 換句話說 R/M 中只有 R/M 和 M/M = $\bigl($ $\overline{0}$ $\bigr)$ 這兩個 ideal 而沒有 nontrivial proper ideal, 所以由 Proposition 6.5.5 知 R/M 是一個 field. 另一方面如果 R/M 是一個 field, 同樣的由 Proposition 6.5.5 我們知 R/M 沒有 nontrivial proper ideal. 因此由我們在 Remark 6.3.6 中提到的比較強(有唯一性)的 Correspondence 定理知沒有其他的 ideal 介於 R 和 M 之間, 故得 M 是 maximal ideal.

我們知道在一個 field 中非 0 的元素都是 unit, 然而 Lemma 5.3.7 告訴我們一個 unit 絕不會是 zero divisor, 所以我們知道一個 field 事實上是一個 integral domain. 痍Y R/M 是一個 field, 則 R/M 是一個 integral domain. 所以由 Theorem 6.5.7 和 Theorem 6.5.11 可得以下之結果:

注意 Corollary 6.5.13 反過來並不一定對. 例如在 $\mathbb {Z}$ 中我們知 $\mathbb {Z}$ / $\bigl($ 0 $\bigr)$ $\simeq$ $\mathbb {Z}$ , 但 $\mathbb {Z}$ 是 integral domain 卻不是 field, 所以知 $\bigl($ 0 $\bigr)$ 是 $\mathbb {Z}$ 的 prime ideal 但不是 maximal ideal.