

下一頁: Finite Abelian Groups
上一頁: 一些常見的 Groups
前一頁: Cyclic Groups
若給定兩個(或更多) groups,
在這節中我們將介紹一種方法可以利用這些 groups 創造出新的 group.
這個方法稱之為 direct product.
Definition 3.2.1
給定兩 groups,
G1 和
G2, 則定義
G1×
G2 = {(
a1,
a2) |
a1  G1
G1,
a2  G2
G2}.
若 (
a1,
a2),
(
b1,
b2)
 G1
G1×
G2, 則定義其乘法為
(a1, a2) . (b1, b2) = (a1 . b1, a2 . b2).
我們稱
G1×
G2 為
G1 和
G2 的
direct product.
事實上利用上述的乘法
G1×G2 是一個 group.
其中封閉性和結合率可以用原來 G1 和 G2
的封閉性與結合濾輕鬆得證. 什麼會是
G1×G2 的 identity 呢?
若 e1 和 e2 分別是 G1 和 G2 的 identity, 應該很容易看出
(e1, e2) 就是
G1×G2 的 identity 吧! 至於 (a1, a2) 的
inverse 是
(a1-1, a2-1) 直接相乘就可得知.
Proposition 3.2.2
若
G1 和
G2 都是 cyclic groups, 且其 order 分別為
n 和
m.
- 若 n 和 m 互質, 則
G1×G2 仍是一個 cyclic
group.
- 若 n 和 m 不互質, 則
G1×G2 不是 cyclic
group.
証 明.
因
G1 和
G2 是 cyclic, 假設
G1 和
G2 分別是由
a 和
b
生成. 注意: 從定義知
G1×
G2 的 order 為
nm.
(1) 假設 n 和 m 互質, 要證明
G1×G2 是 cyclic
我們只要證明
G1×G2 中存在一元素其 order 為 nm.
因為如此一來, 這個元素生成的 group 和
G1×G2 個數一樣多,
所以
G1×G2 就可由其生成. 該找什麼元素呢? 讓我們試試
(a, b) 吧. 由 Lemma 2.3.1 要說 (a, b) 的 order 為 nm,
等同於說 nm 是最小的正整數使得
(a, b)nm = (e1, e2).
首先觀察
(a, b)nm = ((an)m,(bm)n) = (e1m, e2n) = (e1, e2).
接著要說明
nm 是符合上式的最小的正整數. 假設
(
a,
b)
r = (
e1,
e2),
則因
(
a,
b)
r = (
ar,
br), 故得
ar =
e1 且
br =
e2. 因
ord(
a) =
n 且
ord(
b) =
m, 由 Lemma
2.3.2 知
n |
r 且
m |
r. 然而由假設
n 和
m 互質可得
nm |
r, 故若
r
是一個正整數使得
(
a,
b)
r = (
e1,
e2) 則
r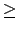 nm
nm. 由此證得 (
a,
b)
的 order 為
nm, 換句話說
G1×
G2 是一個由 (
a,
b) 生成的
cyclic group.
(2) 假設 n 和 m 不互質, 令 l 為 n 和 m 的最小公倍數.
注意因 n 和 m 不互質, 此時 l < nm. 因 a 生成 G1, 故
G1 的元素都可寫成 ai 這種形式. 同理 G2 的元素都可寫成 bj
這種形式. 因此
G1×G2 的元素都可寫成 (ai, bj) 這種形式.
考慮
(ai, bj)l = (ail, bjl).
因
l 是
n 的倍數, 故
ail =
e1. 同理
bjl =
e2. 也就是說
(
ai,
bj)
l = (
e1,
e2).
由 Lemma
2.3.1 知
G1×
G2 中的任一元素 (
ai,
bj) 其
order 小於或等於
l. 所以在
G1×
G2 中找不到一個元素其
order 為
nm. 故
G1×
G2 不可能是 cyclic.

証 明.
由 Proposition
3.2.2 知

/
n
×

/
m
是一個
cyclic group. 然而

/
n
×

/
m
的 order 為
nm, 故由
Theorem
3.1.1 知其和

/(
nm)

isomorphic.

由 Proposition 3.2.2 知道兩個 cyclic groups 的 direct
product 並不一定會依然是 cyclic, 所以 direct product
確實能幫我們產生新的 group. 以後我們可以看到所有的 finite abelian
group 都可以用 cyclic groups 作 direct product 得到.
接下來我們來看看一個 group 若是由其他的 groups 用 direct product
得到, 那麼這一個 group 會有甚麼特性? 若 G1 和 G2 是兩個
groups, 且 e1 和 e2 分別為其 identity. 若
G' = G1×G2,
我們觀察 G' 中兩個很特別的集合:
N' = {(
a,
e2) |
a  G1
G1} and
M' = {(
e1,
b) |
b  G2
G2}.
很容易就可檢查出 N' 和 M' 都是 G' 的 subgroups. 事實上它們都是
G' 的 normal subgroups. 這是因為對於 G' 中的任一元素
(g1, g2), 由於
g1  G1 所以 若 a
G1 所以 若 a  G1 則
g1 . a . g1-1
G1 則
g1 . a . g1-1  G1, 因此
G1, 因此
(
g1,
g2)
. (
a,
e2)
. (
g1,
g2)
-1 = (
g1 . a . g1-1,
g2 . e2 . g2-1) = (
g1 . a . g1-1,
e2)
 N'
N'.
(
g1,
g2)
. (
e1,
b)
. (
g1,
g2)
-1  M'
M'.
我們也很容易看出
N'  G1: 這是因為考慮函數
G1: 這是因為考慮函數
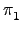 : N
: N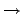 G1
定為
G1
定為
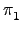 ((a, e2)) = a, 則不難看出
((a, e2)) = a, 則不難看出 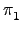 是一個 group
isomorphism. 同理可得
M'
是一個 group
isomorphism. 同理可得
M'  G2. 另外 N' 和 M' 的特點是
G2. 另外 N' 和 M' 的特點是
G =
N' . M' and
N' 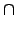 M'
M' = {(
e1,
e2)}.
因為 G' 中的元素都是
(g1, g2) 這種形式, 其中
g1  G1,
g2
G1,
g2  G2. 然而
(g1, e2)
G2. 然而
(g1, e2)  N' 且
(e1, g2)
N' 且
(e1, g2)  M', 故
M', 故
(
g1,
g2) = (
g1,
e2)
. (
e1,
g2)
 N' . M'
N' . M'.
 N'
N'  M', 則由
(g1, g2)
M', 則由
(g1, g2)  N' 得 g2 = e2, 再由
(g1, g2)
N' 得 g2 = e2, 再由
(g1, g2)  M' 得 g1 = e1. 故知
{(e1, e2)} = N'
M' 得 g1 = e1. 故知
{(e1, e2)} = N'  M'.
M'.
Theorem 3.2.4
G  G1
G1×
G2 若且為若
G 中存在兩個 normal subgroups
N
和
M 符合以下條件
-
N
 G1 且
M
G1 且
M  G2.
G2.
-
G = N . M
-
N
 M = {e}, 其中 e 是 G 的 identity.
M = {e}, 其中 e 是 G 的 identity.
証 明.
利用前面所定的
N' 及
M', 我們知
N' 和
M' 是
G1×
G2
的 normal subgroups, 且
N'  G1
G1 及
M'  G2
G2. 我們也知
G1×
G2 =
N' . M' 及
N'  M'
M' = {(
e1,
e2)}.
假設
 : G
: G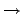 G1×G2 是一個 isomorphism. 則令
G1×G2 是一個 isomorphism. 則令
N = {
a  G
G |

(
a)
 N'
N'} and
M = {
b  G
G |

(
b)
 M'
M'}.
由
Correspondence 定理 (Theorem
2.7.1), 知
N 和
M 都是
G 的
normal subgroups, 又
N/ker(

)
 N'
N' 且
M/ker(

)
 M'
M'. 但因

是一對一, 故由 Lemma
2.5.6 得
ker(

) = {
e}. 因此
再來對於所有
x  G
G, 我們得

(
x)
 G1
G1×
G2, 但因
G1×
G2 =
N' . M', 故知

(
x) =
N' . M'. 也就是說存在
n'  N'
N' 和
m'  M'
M' 使得

(
x) =
n' . m'. 但因

是 onto 的故存在
n  N
N 和
m  M
M 使得

(
n) =
n' 且

(
m) =
m'. 換句話說:

(
x) =

(
n)
. 
(
m) =

(
n . m).
然而

是一對一的故上式得
x =
n . m. 我們得
G 中的任一元素都可寫成
n . m 這種形式, 其中
n  N
N,
m  M
M. 換句話說
G = N . M.
最後, 若
x  N
N  M
M, 則由
x  N
N 得

(
x)
 N'
N',
再由
x  M
M 得

(
x)
 M'
M'. 也就是

(
x)
 N'
N'  M'
M'.
然而已知
N'  M'
M' 是
G1×
G2 的 identity, 故知
x 
ker(

). 再由
ker(

) = {
e} 知
x =
e. 故得證
N 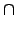 M
M = {
e}.
反知若 G 中存在兩個 normal subgroup N 和 M 滿足 (1), (2), (3).
考慮函數
 : G
: G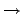 N×M 定義成: 若
x = n . m
N×M 定義成: 若
x = n . m  G, 其中
n
G, 其中
n  N 和 m
N 和 m  M, 則
M, 則
 (x) = (n, m). 這裡要注意
(x) = (n, m). 這裡要注意  是否為
well-defined function? G 中的任一元素由於
G = N . M,
確實可以寫成 n . m 這種形式, 不過寫法唯一嗎? 萬一不唯一, 即
x = n . m = n' . m', 其中 n
是否為
well-defined function? G 中的任一元素由於
G = N . M,
確實可以寫成 n . m 這種形式, 不過寫法唯一嗎? 萬一不唯一, 即
x = n . m = n' . m', 其中 n n' 或 m
n' 或 m m', 則
m', 則
 (x) = (n, m) 又等於 (n', m') 表示
(x) = (n, m) 又等於 (n', m') 表示  是一對多,
那就不是好函數了. 事實上這種寫法是唯一的: 這是因為若
n . m = n' . m' 其中 n, n'
是一對多,
那就不是好函數了. 事實上這種寫法是唯一的: 這是因為若
n . m = n' . m' 其中 n, n'  N, m, m'
N, m, m'  M. 則
M. 則
n'-1 . n = m' . m-1.
然而
n'-1 . n  N
N
且
m' . m-1  M
M, 故知
n'-1 . n  N
N 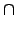 M
M.
再利用假設
N  M
M = {
e} 知
n'-1 . n =
e, 也就是說
n =
n'. 同理可得
m =
m'. 所以寫法唯一. 好了! 既然

是一個好函數, 我們接下來證

是一個 group homomorphism.
也就是若
x =
n . m,
x' =
n' . m' 其中
n,
n'  N
N 且
m,
m'  M
M, 則要證明

(
x . x') =

(
x)
. 
(
x'). 不過
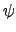
(
x)
. 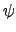
(
x') = (
n,
m)
. (
n',
m') = (
n . n',
m . m'),
如果我們能證明
x . x' = (
n . n')
. (
m . m'), 則由於
n . n'  N
N
且
m . m'  M
M, 故利用

的定義我們有
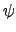
(
x . x') = (
n . n',
m . m').
因此得

(
x . x') =

(
x)
. 
(
x'). 換句話說要證明

是一個 group homomorphism
等於要證
(n . m) . (n' . m') = (n . n') . (m . m').
利用結合率
(n . m) . (n' . m') = n . (m . n') . m'
且
(n . n') . (m . m') = n . (n' . m) . m',
也就是說我們只要證明
m . n' =
n' . m 就可.
要怎麼證
m . n' =
n' . m 呢? 我們知
a =
b 若且為若
a . b-1 =
e. 所以我們考慮
(m . n') . (n' . m)-1 = m . n' . m-1 . n'-1.
然而
m . n' . m-1  N
N
(這是因為
n'  N
N 且
N 是
G 的 normal subgroup), 我們有
m . n' . m-1 . n'-1 = (
m . n' . m-1)
. n'-1  N
N.
同理利用
M 是
G 的
normal subgroup, 我們有
m . n' . m-1 . n'-1 =
m . (
n' . m-1 . n'-1)
 M
M.
因此知
(
m . n')
. (
n' . m)
-1  N
N 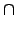 M
M.
再利用
N  M
M = {
e} 得
(
m . n')
. (
n' . m)
-1 =
e, 也就是說
m . n' =
n' . m.
最後我們證

是 1-1 and onto. 若
x 
ker(

), 也就是說

(
x) 是
N×
M 中的 identity (
e,
e) (別忘了
e 是
G 的
identity 所以當然是
N 和
M 的 identity). 因
x  G
G 故存在
n  N
N,
m  M
M 使得
x =
n . m. 由此得

(
x) = (
n,
m) = (
e,
e).
也就是說
n =
e 且
m =
e, 故
x =
e . e =
e. 得證
ker(

) = {
e}
故

是一對一. 要證明

是 onto, 我們必須任取
N×
M
中的任一元素 (
n,
m), 然後說
G 中存在一元素
x 使得

(
x) = (
n,
m). 我們只要令
x =
n . m 即可, 因為由定義此時

(
x) = (
n,
m). 好了我們證得

是一個 isomorphism 故
G 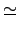 N
N×
M.
不過我們不是該證
G  G1
G1×
G2 嗎? 沒關係,
因為由假設
N  G1
G1 且
M  G2
G2, 利用下一個 Lemma,
我們就可知
G 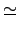 N
N×
M 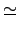 G1
G1×
G2.

証 明.
由假設我們之存在 isomorphisms:
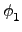
:
G1 G1
G1', 且
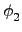
:
G2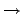 G2
G2'. 定義新的函數

:
G1×
G2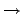 G1
G1'×
G2',
使得對所有的
(
g1,
g2)
 G1
G1×
G2,

((
g1,
g2)) = (
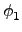
(
g1),
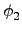
(
g2)).
因為
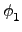
(
g1)
 G1
G1',
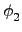
(
g2)
 G2
G2',

真的把
G1×
G2
的元素送到
G1'×
G2'. 利用
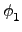
和
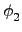
是 group
homomorphism, 我們很容易驗證

也是一個 group homomorphism.
 是 onto 的嗎? 若
(y1, y2)
是 onto 的嗎? 若
(y1, y2)  G1'×G2', 即
y1
G1'×G2', 即
y1  G1' 且
y2
G1' 且
y2  G2', 則因
G2', 則因 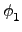 和
和 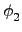 是 onto, 故存在
x1
是 onto, 故存在
x1  G1 且
x2
G1 且
x2  G2 使得
G2 使得
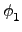 (x1) = y1 且
(x1) = y1 且
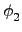 (x2) = y2. 故選
(x1, x2)
(x2) = y2. 故選
(x1, x2)  G1×G2, 則
G1×G2, 則

((
x1,
x2)) = (
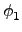
(
x1),
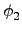
(
x2)) = (
y1,
y2).
所以

是 onto.
什麼是
ker( ) 呢? 若
(a, b)
) 呢? 若
(a, b)  ker(
ker( ), 因
G1'×G2' 的 identity 是
(e1', e2'), 其中 e1' 和 e2' 分別是
G1' 和 G2' 的 identity, 故得
), 因
G1'×G2' 的 identity 是
(e1', e2'), 其中 e1' 和 e2' 分別是
G1' 和 G2' 的 identity, 故得

((
a,
b)) = (
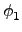
(
a),
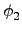
(
b)) = (
e1',
e2').
由此知
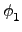
(
a) =
e1' 且
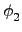
(
b) =
e2'. 換句話說
a 
ker(
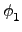
)
且
b 
ker(
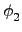
). 然而
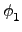
和
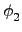
由假設都是一對一的, 故
ker(
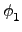
) = {
e1} 且
ker(
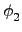
) = {
e2}, 其中
e1 和
e2 分別是
G1 和
G2
的 identity. 故得
a =
e1,
b =
e2, 換句話說
ker(

) 是
G1×
G2 的 identity, 故由 Lemma
2.5.6 知

是一對一的. 因而得證

是一個 isomorphism, 即
G1×
G2 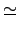 G1
G1'×
G2'.

我們已了解兩個 group 的 direct product 相關的性質, 其實兩個 groups
G1 和 G2 的 direct product
G1×G2 仍是一個 group
所以還可以和第三個 group G3 作 direct product 得
(G1×G2)×G3. 這樣一直推演下去, 可以得到任意 n 個 groups 的
direct product.


下一頁: Finite Abelian Groups
上一頁: 一些常見的 Groups
前一頁: Cyclic Groups
Administrator
2005-06-18
![]() G1: 這是因為考慮函數
G1: 這是因為考慮函數
![]() : N
: N![]() G1
定為
G1
定為
![]() ((a, e2)) = a, 則不難看出
((a, e2)) = a, 則不難看出 ![]() 是一個 group
isomorphism. 同理可得
M'
是一個 group
isomorphism. 同理可得
M' ![]() G2. 另外 N' 和 M' 的特點是
G2. 另外 N' 和 M' 的特點是
![]() : G
: G![]() G1×G2 是一個 isomorphism. 則令
G1×G2 是一個 isomorphism. 則令
![]() : G
: G![]() N×M 定義成: 若
x = n . m
N×M 定義成: 若
x = n . m ![]() G, 其中
n
G, 其中
n ![]() N 和 m
N 和 m ![]() M, 則
M, 則
![]() (x) = (n, m). 這裡要注意
(x) = (n, m). 這裡要注意 ![]() 是否為
well-defined function? G 中的任一元素由於
G = N . M,
確實可以寫成 n . m 這種形式, 不過寫法唯一嗎? 萬一不唯一, 即
x = n . m = n' . m', 其中 n
是否為
well-defined function? G 中的任一元素由於
G = N . M,
確實可以寫成 n . m 這種形式, 不過寫法唯一嗎? 萬一不唯一, 即
x = n . m = n' . m', 其中 n![]() n' 或 m
n' 或 m![]() m', 則
m', 則
![]() (x) = (n, m) 又等於 (n', m') 表示
(x) = (n, m) 又等於 (n', m') 表示 ![]() 是一對多,
那就不是好函數了. 事實上這種寫法是唯一的: 這是因為若
n . m = n' . m' 其中 n, n'
是一對多,
那就不是好函數了. 事實上這種寫法是唯一的: 這是因為若
n . m = n' . m' 其中 n, n' ![]() N, m, m'
N, m, m' ![]() M. 則
M. 則
![]() 是 onto 的嗎? 若
(y1, y2)
是 onto 的嗎? 若
(y1, y2) ![]() G1'×G2', 即
y1
G1'×G2', 即
y1 ![]() G1' 且
y2
G1' 且
y2 ![]() G2', 則因
G2', 則因 ![]() 和
和 ![]() 是 onto, 故存在
x1
是 onto, 故存在
x1 ![]() G1 且
x2
G1 且
x2 ![]() G2 使得
G2 使得
![]() (x1) = y1 且
(x1) = y1 且
![]() (x2) = y2. 故選
(x1, x2)
(x2) = y2. 故選
(x1, x2) ![]() G1×G2, 則
G1×G2, 則
![]() ) 呢? 若
(a, b)
) 呢? 若
(a, b) ![]() ker(
ker(![]() ), 因
G1'×G2' 的 identity 是
(e1', e2'), 其中 e1' 和 e2' 分別是
G1' 和 G2' 的 identity, 故得
), 因
G1'×G2' 的 identity 是
(e1', e2'), 其中 e1' 和 e2' 分別是
G1' 和 G2' 的 identity, 故得