next up previous
下一頁: Roots of Polynomials 上一頁: 中級 Field 的性質 前一頁: Algebraic Elements

Algebraic Closure

當 F 是一個 field, L 是 F 的一個 extension 時, 我們可以將 L 中的元素分成 algebraic over F 和不是 algebraic over F 的兩種. 在這一節中我們將探討 L 中所有 algebraic over F 的元素所成之集合.

Definition 10.2.1   假設 F 是一個 field 且 L 是 F 的一個 extension. 我們令

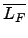
$\displaystyle \overline{L_F}$ = {a $\displaystyle \in$ L | a 是 algebraic over F},

稱之為 F 在 L 的 algebraic closure.

F 中的元素當然是 algebraic over F, 所以由定義知 F $ \subseteq$ $ \overline{L_F}$ $ \subseteq$ L. 另� 如果 L 是 F 的一個 finite extension, 則由 Lemma 9.4.5 知 L 中的元素都 algebraic over F, 所以在這個假設之下 $ \overline{L_F}$ = L.

接下來我們要證明 $ \overline{L_F}$ 的一個重要性質, 即 $ \overline{L_F}$ 是一個 field. 換言之, 我們要證明若 a, b $ \in$ $ \overline{L_F}$, 其中 b$ \ne$ 0, 則 a - b 以及 a . b-1 皆在 $ \overline{L_F}$ 中 (Lemma 9.1.4). 要如何證明這些元素都是 algebraic over F 呢? 當然不可能用找 polynomial 的方法, 我們必須藉助 Theorem 10.1.9. 在這之前我們先推廣一下 Definition 10.1.6.

Definition 10.2.2   假設 F 是一個 field 且 L 是 F 的一個 extension. 若 a1,..., an $ \in$ L, 則定 F(a1,..., an) 表示為 L 中包含 F 以及 a1,..., an 最小的 field.

Lemma 10.2.3   假設 F 是一個 field 且 L 是 F 的一個 extension. 若 a1,..., an $ \in$ L 皆為 algebraic over F, 則 F(a1,..., an) 是 F 的一個 finite extension. 事實上, 如果已知 a1,..., an over F 的 degree 分別為 m1,..., mn, 則

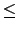[F(a1,..., an) : F]$\displaystyle \le$m1 ... mn.

証 明. 為了方便, 我們令

K1 = F(a1), K2 = K1(a2) = F(a1, a2),..., Kn = Kn - 1(an) = F(a1,..., an).

對任意的 i, 我們有 [Ki : Ki - 1] = [Ki - 1(ai) : Ki]$ \le$mi. 這裡 [Ki - 1(ai) : Ki - 1] 會小於或等於 mi 的原因是: 由 Corollary 10.1.7 知 [Ki - 1(ai) : Ki - 1] 的值剛好是 ai over Ki - 1 的 minimal polynomial qi(x) $ \in$ Ki - 1[x] 的 degree. 然而由假設 ai over F 的 minimal polynomial pi(x) $ \in$ F[x] 的 degree 為 mi. 由於 pi(x) $ \in$ F[x] $ \subseteq$ Ki - 1[x] 且 pi(ai) = 0, 故由 qi(x) 是 ai over Ki - 1 的 minimal polynomial 的假設知 deg(qi(x))$ \le$deg(pi(x)) = mi. 故知

[Ki : Ki - 1] = [Ki - 1(ai) : Ki - 1] = deg(qi(x))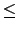$\displaystyle \le$mi.

畢b由於每一段 [Ki : Ki - 1] 都是有限的, 所以我們可以連續套用 Theorem 9.4.6 得:

[F(a1,..., an) : F] = [Kn : Kn - 1][Kn - 1 : F]  
  = [Kn : Kn - 1][Kn - 1 : Kn - 2][Kn - 2 : F]  
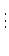  $\displaystyle \vdots$    
  = [Kn : Kn - 1] ... [K1 : F]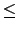$\displaystyle \le$mn ... m1.  

故得證 F(a1,..., an) 是 F 的一個 finite extension. $ \qedsymbol$

利用 Lemma 10.2.3 我們馬上可得知 $ \overline{L_F}$ 是一個 field.

Theorem 10.2.4   假設 F 是一個 field 且 L 是 F 的一個 extension. 若 a, b $ \in$ L, 其中 b$ \ne$ 0, 皆為 algebraic over F, 則 a + b, a - b, a . b 以及 a . b-1 皆為 algebraic over F. 由此我們可得 $ \overline{L_F}$ 是一個 field.

証 明. 由 Lemma 10.2.3 我們知 F(a, b) 是 F 的一個 finite extension. 由於 a, b $ \in$ F(a, b), b$ \ne$ 0 且 F(a, b) 是一個 field, 我們自然有 a + b, a - b, a . b 以及 a . b-1 皆為 F(a, b) 的元素. 故由 Theorem 10.1.9 (或 Lemma 10.1.3) 知這四個元素皆為 algebraic over F.

今若 a, b $ \in$ $ \overline{L_F}$, 其中 b$ \ne$ 0, 則由定義知 a, b 皆為 algebraic over F. 故由前知 a + b, a - b, a . b 以及 a . b-1 皆為 algebraic over F. 故知這四個元素皆在 $ \overline{L_F}$ 中, 因此得證 $ \overline{L_F}$ 是一個 field. $ \qedsymbol$

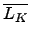假設 L 是 F 的一個 extension, 且 K 是 L over F 的 subextension (即 F $ \subseteq$ K $ \subseteq$ L). L 中是 algebraic over K 的元素未必是 algebraic over F. 不過 L 中是 algebraic over F 的元素就一定是 algebraic over K. 這是因為若 a $ \in$ $ \overline{L_F}$ (即 a $ \in$ L 是 algebraic over F), 表示在 F[x] 中存在 f (x)$ \ne$ 0 使得 f (a) = 0. 由於 f (x) $ \in$ F[x] $ \subseteq$ K[x], 我們自然得 a 也是 algebraic over K. 故得 a $ \in$ $ \overline{L_K}$, 換句話說我們總是有

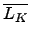$\displaystyle \overline{L_F}$ $\displaystyle \subseteq$ $\displaystyle \overline{L_K}$.

我們有興趣知道什麼時候 $ \overline{L_F}$ 會等於 $ \overline{L_K}$. 以下是一個例子.

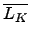
Lemma 10.2.5   假設 F 是一個 field, L 是 F 的一個 extension, 且 K 是 L over F 的 subextension. 若 K 是 F 的一個 finite extension, 則 $ \overline{L_F}$ = $ \overline{L_K}$

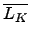
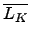
証 明. 我們已知 $ \overline{L_F}$ $ \subseteq$ $ \overline{L_K}$, 所以只要證明 $ \overline{L_K}$ $ \subseteq$ $ \overline{L_F}$. 也就是要證明: 若 a $ \in$ L 是 algebraic over K, 則 a 是 algebraic over F. 我們考� K(a) 這一個 field. 由假設 a 是 algebraic over K, 故利用 Corollary 10.1.7 知 K(a) 是 K 的一個 finite extension. 再加上 K 是 F 的一個 finite extension, 套用 Theorem 9.4.6 可得

[K(a) : F] = [K(a) : K][K : F],

因此 K(a) 是 F 的一個 finite extension. 故利用 a $ \in$ K(a) 以及 Theorem 10.1.9 (或 Lemma 10.1.3) 知 a 是 algebraic over F. $ \qedsymbol$

我們可以將 Lemma 10.2.5 推廣到更一般的狀況. 回顧一下若 K 是 F 的一個 algebraic extension 表示 K 中的元素皆為 algebraic over F. 在 Lemma 10.2.5 中的假設 K 是 F 的 finite extension, 所以自然是 F 的一個 algebraic extension. 我們要將 Lemma 10.2.5 推廣到 K 是 F 的 algebraic extension 這個狀況.

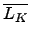
Theorem 10.2.6   假設 F 是一個 field, L 是 F 的一個 extension, 且 K 是 L over F 的 subextension. 若 K 是 F 的一個 algebraic extension, 則 $ \overline{L_F}$ = $ \overline{L_K}$

証 明. 和 Lemma 10.2.5 相同的情形, 我們只要證明: 若 a $ \in$ L 是 algebraic over K, 則 a 是 algebraic over F. 不過這裡碰到的狀況是 K 可能不是 finite extension over F, 所以我們不能直接套用 Lemma 10.2.5. 要克服這個困難, 我們必須想辦法找到一個 F 的 finite extension K' 且滿足 a 是 algebraic over K'. 如此再套用 Lemma 10.2.5 得證 a 是 algebraic over F.

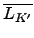由假設 a 是 algebraic over K, 知存在 f (x)$ \ne$ 0 且 f (x) $ \in$ K[x] 使得 f (a) = 0. 假設 f (x) = anxn + ... + a0. 由於 an,..., a0 $ \in$ K 且 K 是 F 的一個 algebraic extension, 故知 an,..., a0 皆為 algebraic over F. 令 K' = F(an,..., a0), 由 Lemma 10.2.3 知 K' 是 F 的一個 finite extension. 故利用 Lemma 10.2.5 知 $ \overline{L_{K'}}$ = $ \overline{L_F}$. 另� 由於 an,..., a0 $ \in$ F(an,..., a0) = K', 我們知 f (x) $ \in$ K'[x]. 故由 f (a) = 0 知 a 是 algebraic over K'. 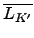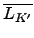換言之, 我們有 a $ \in$ $ \overline{L_{K'}}$, 故由 $ \overline{L_{K'}}$ = $ \overline{L_F}$ 得知 a $ \in$ $ \overline{L_F}$. 因此得證 a 是 algebraic over F. $ \qedsymbol$

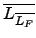我們已知 $ \overline{L_F}$ 是一個 filed (Theorem 10.2.4) 且 F $ \subseteq$ $ \overline{L_F}$ $ \subseteq$ L. 如果我們再收集 L 中是 algebraic over $ \overline{L_F}$ 的元素會不會得到更大的 field 的呢? 換句話來說, 我們想知道 $ \overline{L_{\overline{L_F}}}$ (不要被這符號� 著了) 是什麼? 事實上所謂的 algebraic closure 就是說 L 中 algebraic over $ \overline{L_F}$ 的元素所成的集合就是 $ \overline{L_F}$ 自己.

Corollary 10.2.7   假設 F 是一個 field 且 L 是 F 的一個 extension, 若 a $ \in$ L 且 a 是 algebraic over $ \overline{L_F}$, 則 a 是 algebraic over F. 也就是說, 我們有

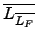
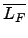
$\displaystyle \overline{L_{\overline{L_F}}}$ = $\displaystyle \overline{L_F}$.

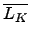
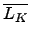
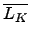
証 明. 首先注意由定義 $ \overline{L_F}$ 中的元素都是 algebraic over F, 故知 $ \overline{L_F}$ 是 F 的一個 algebraic extension. 因此若令 K = $ \overline{L_F}$, 則 K 符合 Theorem 10.2.6 的條件, 故知 $ \overline{L_K}$ = $ \overline{L_F}$. 也因此若 a $ \in$ L 是 algebraic over $ \overline{L_F}$ = K, 表示 a $ \in$ $ \overline{L_K}$. 故由 $ \overline{L_K}$ = $ \overline{L_F}$ 得知 a $ \in$ $ \overline{L_F}$, 也就是說 a 是 algebraic over F. $ \qedsymbol$

next up previous
下一頁: Roots of Polynomials 上一頁: 中級 Field 的性質 前一頁: Algebraic Elements
Administrator 2005-06-18