


§U§@≠∂: Finite Fields
§W§@≠∂: §§ĮŇ Field ™ļ© ĹŤ
ęe§@≠∂: Algebraic Closure
≥o§@ł`§§ßŕ≠ŐĪNįQĹ◊§@≠” polynomial ¶b§@≠” field §§•¶™ļģŕ™ļ© ĹŤ.
≠ļ•żßŕ≠ŐŃŔ¨O®”¨›§jģa≥ŐľŰĪx™ļĺl¶°©w≤z.
Lemma 10.3.1
į≤≥]
F ¨O§@≠” field. ≠Y
f (
x)
 F
F[
x], ®š§§
deg(
f (
x)) =
n, •B
a  F
F ļ°®¨
f (
a) = 0, ęh¶s¶b
h(
x)
 F
F[
x], ®š§§
deg(
h(
x)) =
n - 1, ®ŌĪo
f (
x) = (
x -
a)
. h(
x).
Ķż ©ķ.
•—©ů
F ¨O§@≠” field, ¶“ľ
f (
x)
 F
F[
x] •H§ő
(
x -
a)
 F
F[
x],
ßQ•ő Euclid's Algorithm (Theorem
7.2.4) ™ĺ¶s¶b
h(
x),
r(
x)
 F
F[
x] ļ°®¨
f (
x) = (
x -
a)
. h(
x) +
r(
x), ®š§§
r(
x) = 0 ©ő
deg(
r(
x)) < deg(
x -
a) = 1. ¶p™G
r(
x)

0 •—
deg(
r(
x)) < 1 ™ĺ
r(
x) =
c  F
F ¨O§@≠”Ī`ľ∆. ¶ż•—©ů
f (
a) = 0 ¨GĪN
a •N§J
f (
x) = (
x -
a)
. h(
x) +
c Īo
c = 0, ¶Ļ©M
r(
x)

0 ¨Ř•Ŕ¨ř¨G™ĺ
r(
x) = 0. §]īN¨O
f (
x) = (
x -
a)
. h(
x). ¶‹©ů
deg(
h(
x)) =
n - 1, •i•—
Lemma
7.2.2 ™ĹĪĶĪo™ĺ.

•—©ů
deg(x - a) = 1, ßŕ≠Ő™ĺĻD x - a ¨O F[x] §§™ļ irreducible
element. ¶]¶Ļ Lemma 10.3.1 ßi∂Dßŕ≠Ő≠Y f (a) = 0, ęh x - a ∑|¨O
f (x) ™ļ§@≠” irreducible divisor. ßQ•ő F[x] ¨O unique
factorization domain (Theorem 7.2.14), ßŕ≠Ő™ĺ¶s¶b
k 
 •H§ő
q(x)
•H§ő
q(x)  F[x] ®ŌĪo
f (x) = (x - a)k . q(x), ®š§§ q(a)
F[x] ®ŌĪo
f (x) = (x - a)k . q(x), ®š§§ q(a) 0
(ßY x - a §£¨O q(x) ™ļ divisor). ßŕ≠Ő®Ő¶Ļ®”©włq a ¶b f (x)
™ļ≠ęģŕľ∆.
0
(ßY x - a §£¨O q(x) ™ļ divisor). ßŕ≠Ő®Ő¶Ļ®”©włq a ¶b f (x)
™ļ≠ęģŕľ∆.
Definition 10.3.2
į≤≥]
F ¨O§@≠” field. ≠Y
f (
x)
 F
F[
x] •B
a  F
F ļ°®¨
f (
a) = 0,
ęhļŔ
a ¨O§@≠”
root of
f (
x). §S¶p™G
f (
x) = (
x -
a)
k . q(
x), ®š§§
q(
a)

0, ęhļŔ
a ¨O§@≠”
root of
multiplicity k of
f (
x).
ĪĶ§U®”§]¨O§jģaľŰĪx™ļ©w≤z: §@≠” n ¶ł¶h∂Ķ¶°¶b§@≠” field
§§≠pļ‚≠ęģŕ¶b§ļ¶‹¶h¶≥ n ≠”ģŕ. ≥ołŐ꣙ļ≠pļ‚≠ęģŕ¶b§ļ¨OĽ°¶p™G a ¨O
k ≠ęģŕ, ęh≠nļ‚¶®¨O k ≠”ģŕ.
Theorem 10.3.3
į≤≥]
F ¨O§@≠” field. ≠Y
f (
x)
 F
F[
x] •B
deg(
f (
x)) =
n
1,
ęh¶b
F §§ĪN multiplicity ≠pļ‚¶b§ļ,
f (
x) ¶‹¶h¶≥
n ≠” roots.
Ķż ©ķ.
ßŕ≠ŐßQ•ő induction. ¶p™G
deg(
f (
x)) = 1, ęh
f (
x) ∑ŪĶM∂»¶≥ 1
≠”ģŕ. į≤≥] degree §p©ů
n ™ļ polynomial ©w≤z¨“¶®•Ŗ. ≤¶“ľ
f (
x)
 F
F[
x] •B
deg(
f (
x)) =
n ™ļĪ°ßő. ¶p™G
f (
x) ¶b
F §§®S¶≥ root,
ęh©w≤z∑ŪĶM¶®•Ŗ. ¶p™G
a  F
F ¨O
f (
x) ™ļ§@≠” root of multiplicity
k, ßY™Ū•‹¶s¶b
q(
x)
 F
F[
x] ®ŌĪo
f (
x) = (
x -
a)
k . q(
x), ®š§§
q(
a)

0. ßQ•ő degree ™ļ© ĹŤ (Lemma
7.2.2) ßŕ≠Ő¶≥
deg(
q(
x)) =
n -
k <
n, ¨GßQ•ő induction ™ļį≤≥]™ĺ¶b
F §§ĪN
multiplicity ≠pļ‚¶b§ļ,
q(
x) ¶‹¶h¶≥
n -
k ≠” roots. ĶM¶”≠Y
b  F
F
¨O
f (
x) ™ļ§@≠” root, ßŕ≠Ő¶≥
0 = f (b) = (b - a)k . q(b).
ßQ•ő
F
¨O integral domain, ßŕ≠Ő™ĺ
f (
x) ™ļ roots ≠n§£¨O
a īN¨O
q(
x) ™ļ
roots. ¶]¶Ļ¶b
F §§
f (
x) roots ™ļ≠”ľ∆īN¨O
k •[§W
q(
x) ™ļ
roots ™ļ≠”ľ∆, ©“•H¶‹¶h¶≥
k + (
n -
k) =
n ≠”.

ßŕ≠Ő≠n¨›§@≠”§łĮņ a ¨Oß_¨O f (x) ™ļ§@≠”ģŕ, §jģa™ĹńĪ™ļ∑Q™kīN¨OĪN
a •N§J f (x) ¨›¨Oß_¨į 0. ®∆ĻͧW≥o¨O§£ĻÔ™ļ, ≠nĪN a •N§J f (x)
≤oߍ§W a ©M f (x) ™ļęYľ∆∂°™ļ•[™k©M≠ľ™k. īꮕ§ß¶p™G a
ģył®¶b§@≠”•]ßt F ©M a ™ļ field L (¶‹§÷≠n¨O ring) §§,
≥oľňßŕ≠Ő§ •i•HĪN a ©M f (x) ™ļęYľ∆¶“ľ¶®¨O L ™ļ§łĮņ¶”•[•HĻBļ‚.
≥oľň f (a) (¨›¶®¨O L ™ļ§łĮņ) § ¶≥∑Nłq.
≥oīN¨O¨į¨∆ĽÚßŕ≠Őęe≠Ī™ļįQĹ◊≥£∑|•żĶĻ F ™ļ§@≠” extension L,
ĶMꊶAĹÕĹ◊ a  L ĽP F[x] §§™ļ polynomials ™ļ√ŲęY.
©“•Hßŕ≠Ő¶ŘĶM∑|į›: ĶĻ©w•Ű§@ęDĪ`ľ∆™ļ
f (x)
L ĽP F[x] §§™ļ polynomials ™ļ√ŲęY.
©“•Hßŕ≠Ő¶ŘĶM∑|į›: ĶĻ©w•Ű§@ęDĪ`ľ∆™ļ
f (x)  F[x] ¨Oß_•i•Hßš®ž F
™ļ§@≠” extension L ®ŌĪo f (x) ¶b L §§¶≥ģŕ? Ķ™ģ◊¨O™÷©w™ļ.
•H§U™ļ©w≤zīN¨O¶^Ķ™≥o≠”į›√D. ßŕ≠ŐĪN∑|ęōļc§@≠” F ™ļ extension field
ĶMꊼ°©ķ¶b®š§§•ißš®ž§@≠”ģŕ. ≥o≠”©w≤z™ļ√“©ķ¶Pĺ«©ő≥|ńĪĪo``ĶÍĶÍ''™ļ,
¶]¨į¶nĻ≥®S¶≥Įu™ļ¶bßšģŕ™ļ∑PńĪ.
§£ĻL≥oīN¨Oľ∆嫶bĹÕ¶s¶b© ©“√Ų§Ŗ™ļ≠ę¬I,
ßŕ≠Ő•u≠n™ĺĻD™F¶Ť¶s¶b¶”§£•≤Įu•Ņßi∂DßA™F¶Ť¨O§įĽÚ.
F[x] ¨Oß_•i•Hßš®ž F
™ļ§@≠” extension L ®ŌĪo f (x) ¶b L §§¶≥ģŕ? Ķ™ģ◊¨O™÷©w™ļ.
•H§U™ļ©w≤zīN¨O¶^Ķ™≥o≠”į›√D. ßŕ≠ŐĪN∑|ęōļc§@≠” F ™ļ extension field
ĶMꊼ°©ķ¶b®š§§•ißš®ž§@≠”ģŕ. ≥o≠”©w≤z™ļ√“©ķ¶Pĺ«©ő≥|ńĪĪo``ĶÍĶÍ''™ļ,
¶]¨į¶nĻ≥®S¶≥Įu™ļ¶bßšģŕ™ļ∑PńĪ.
§£ĻL≥oīN¨Oľ∆嫶bĹÕ¶s¶b© ©“√Ų§Ŗ™ļ≠ę¬I,
ßŕ≠Ő•u≠n™ĺĻD™F¶Ť¶s¶b¶”§£•≤Įu•Ņßi∂DßA™F¶Ť¨O§įĽÚ.
Theorem 10.3.4
į≤≥]
F ¨O§@≠” field •B
p(
x)
 F
F[
x] ¨O
F[
x] §§™ļ irreducible
element, ęh¶s¶b§@≠” field
L ¨O
F ™ļ finite extension, ®š§§
[
L :
F] = deg(
p(
x)) •B
L §§¶s¶b
a  L
L ļ°®¨
p(
a) = 0.
Ķż ©ķ.
•O
L =
F[
x]/
 p
p(
x)

. •—©ů
p(
x) ¨O irreducible, ßŕ≠Ő™ĺ
 p
p(
x)

¨O
F[
x] §§™ļ maximal ideal, ¨G™ĺ
L ¨O§@≠” field.
≠ļ•żßŕ≠Ő≠nŇÁ√“ L §§¶s¶b§@≠” subfield ©M F ¨O isomorphic ™ļ,
¶]¶Ļßŕ≠Ő•i•HĪN L ¨›¶®¨O F ™ļ§@≠” extension. ®∆ĻͧW¶“ľ
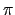 : F
: F F[x]/
F[x]/ p(x)
p(x) , ©włq¶®
, ©włq¶®
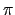 (c) =
(c) = 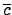 , ę‹ģe©ŲŇÁ√“
, ę‹ģe©ŲŇÁ√“ 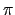 ¨O§@≠”
ring homomorphism. §]ę‹ģe©ŲŇÁ√“
¨O§@≠”
ring homomorphism. §]ę‹ģe©ŲŇÁ√“ 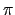 ¨O§@ĻÔ§@™ļ: ≥o¨O¶]¨į¶p™G
c
¨O§@ĻÔ§@™ļ: ≥o¨O¶]¨į¶p™G
c  ker(
ker(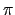 ), ™Ū•‹
), ™Ū•‹
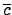 =
=  , ßY
c
, ßY
c 
 p(x)
p(x) . ¶ż¨O
. ¶ż¨O
 p(x)
p(x) §§į£§F 0 •H• ®S¶≥®š•L™ļĪ`ľ∆, ¨GĪo c = 0 (§]•iģM•ő
Proposition 9.1.5 (2) Īo®ž
§§į£§F 0 •H• ®S¶≥®š•L™ļĪ`ľ∆, ¨GĪo c = 0 (§]•iģM•ő
Proposition 9.1.5 (2) Īo®ž 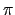 ¨O§@ĻÔ§@). ¶]¶ĻĪo√“
im(
¨O§@ĻÔ§@). ¶]¶ĻĪo√“
im(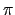 ) ¨O L ™ļ subfield •B©M F ¨O isomorphic ™ļ.
) ¨O L ™ļ subfield •B©M F ¨O isomorphic ™ļ.
≤¶b≠n√“©ķ L §§¶s¶b§@§łĮņ¨O p(x) ™ļģŕ. ¶“ľ
a = 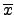
 L,
ßŕ≠Ő≠nĽ°©ķ
p(
L,
ßŕ≠Ő≠nĽ°©ķ
p(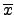 ) =
) =  (™`∑N
(™`∑N
 ¨O
L = F[x]/
¨O
L = F[x]/ p(x)
p(x) ™ļ 0). į≤≥]
p(x) = anxn + ... + a1x + a0, ®š§§ ai
™ļ 0). į≤≥]
p(x) = anxn + ... + a1x + a0, ®š§§ ai  F. ®ļĽÚ
p(a) ∑|¨O§įĽÚ©O? ßOß—§Fßŕ≠Őī£ĻL≥ołŐ•N§J a •≤∂∑•ő®ž™ļ¨O L
§§™ļĻBļ‚, ¶”¶b L §§ c
F. ®ļĽÚ
p(a) ∑|¨O§įĽÚ©O? ßOß—§Fßŕ≠Őī£ĻL≥ołŐ•N§J a •≤∂∑•ő®ž™ļ¨O L
§§™ļĻBļ‚, ¶”¶b L §§ c  F ¨OĽ›łgĻL
F ¨OĽ›łgĻL 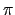 įe®ž L ™ļ,
īę•ył‹Ľ°ßŕ≠Ő•≤∂∑¶“ľ™ļ¨O
įe®ž L ™ļ,
īę•ył‹Ľ°ßŕ≠Ő•≤∂∑¶“ľ™ļ¨O
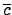 . ¶]¶Ļ¶≥
. ¶]¶Ļ¶≥
| p(a) |
= |
p(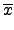 ) ) |
|
| |
= |
an . 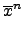 + ... + a1 . + ... + a1 . 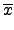 + a0 + a0 |
|
| |
= |
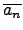 . . 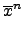 + ... + + ... + 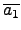 . . 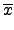 + + 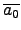 ( ( ) ) |
|
| |
= |
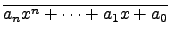 |
|
| |
= |
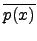 = =  |
|
©“•H
L §§Įu™ļ¶s¶b§@≠”§łĮņ•N§J
p(
x) Ķ•©ů
L §§™ļ 0.
≥Őꊕ— Lemma 9.3.6 ™ĺ
[L : F] = dimF(L) = dimF(F[x]/ p(x)
p(x) ) = deg(p(x)).
) = deg(p(x)). 
•— Theorem 10.3.4 ßŕ≠Őę‹ģe©ŲĪo®ž•H§U§@ĮŽ™ļ™¨™p.
Corollary 10.3.5
į≤≥]
F ¨O§@≠” field •B
f (
x)
 F
F[
x], ®š§§
deg(
f (
x)) =
n
1,
ęh¶s¶b§@≠” field
L ¨O
F ™ļ finite extension, ®š§§
[
L :
F]
 n
n
•B
L §§¶s¶b
a  L
L ļ°®¨
f (
a) = 0.
Ķż ©ķ.
•—©ů
f (
x)
 F
F[
x] ¶”•B
deg(
f (
x))

1, ©“•H
f (
x) §£¨O
F[
x]
§§™ļ unit. ßQ•ő
F[
x] ¨O unique factorization domain, ßŕ≠Ő™ĺ¶s¶b
p(
x)
 F
F[
x] ¨O
F[
x] §§™ļ irreducible element ļ°®¨
p(
x) |
f (
x). ™`∑N¶p™G
p(
a) = 0, ęh∑ŪĶMĪo
f (
a) = 0. ¶]¶Ļ•— Theorem
10.3.4 ™ĺ¶s¶b
L, ®š§§
[
L :
F] = deg(
p(
x))

deg(
f (
x)) •B
a  L
L, ļ°®¨
f (
a) =
p(
a) = 0.

ßŕ≠Ő•i•H§@™ĹģM•ő Corollary 10.3.5 ßš®ž§@≠” F ™ļ finite
extension L' ®ŌĪo f (x) ¶b L' §§•i•HßĻ•Ģ§ņł—. ≥ołŐ©“Ņ◊™ļ f (x)
¶b L' ßĻ•Ģ§ņł—īN¨OĽ°: ¶p™G
deg(f (x)) = n, ęh f (x) ¶b L'[x]
§§•i•Hľg¶®
f (x) = c . (x - a1) ... (x - an), ®š§§ ai  L'.
¶Ļģ…ßŕ≠Ő≥qĪ`ļŔ f (x) splits into linear factors in L'.
L'.
¶Ļģ…ßŕ≠Ő≥qĪ`ļŔ f (x) splits into linear factors in L'.
Theorem 10.3.6
į≤≥]
F ¨O§@≠” field •B
f (
x)
 F
F[
x], ®š§§
deg(
f (
x)) =
n
1,
ęh¶s¶b§@≠” field
L' ¨O
F ™ļ finite extension, ®š§§
[
L' :
F]
 n
n!, ®ŌĪo
f (
x) splits into linear factors in
L'.
Ķż ©ķ.
ßQ•ő Corollary
10.3.5 ™ĺ¶s¶b
L1 ¨O
F ™ļ§@≠” extension
ļ°®¨
[
L1 :
F]
 n
n •B
a1  L1
L1 ®ŌĪo
f (
a1) = 0. ¨G•— Lemma
10.3.1 ™ĺ¶s¶b
f1(
x)
 L1
L1[
x] •B
deg(
f1(
x)) =
n - 1 ®ŌĪo
f (
x) = (
x -
a1)
. f1(
x). ĻÔ
f1(
x) ¶AģM•ő§@¶ł Corollary
10.3.5 ™ĺ¶s¶b
L2 ¨O
L1 ™ļ§@≠” extension ļ°®¨
[
L2 :
L1]
 n
n - 1 •B
a2  L2
L2 ®ŌĪo
f1(
a2) = 0. ™`∑N¶Ļģ…
[
L2 :
F] = [
L2 :
L1][
L1 :
F]
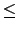 n
n(
n - 1),
•B¶s¶b
f2(
x)
 L2
L2[
x]
®ŌĪo
f (x) = (x - a1) . (x - a2) . f2(x).
©“•H≥oľň§@™Ĺß@§U•h
(©ő¨OĻÔ degree ß@ induction) ßŕ≠ŐĪo√“•Ľ©w≤z.

≥ŐęŠßŕ≠ŐĪjĹ’§@§U Theorem 10.3.6 łŐ™ļ L' ∑ŪĶM∑|¶] f (x)
§£¶P¶”§£¶P, §£ĻL®∆ĻͧWßŕ≠Ő•i•Hßš®ž§@≠” F ™ļ extension 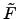 ®ŌĪo F[x] §§™ļ©“¶≥ polynomial ¶b
®ŌĪo F[x] §§™ļ©“¶≥ polynomial ¶b 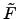 §§≥£•i•H splits into
linear factors (∑ŪĶM¶Ļģ…
§§≥£•i•H splits into
linear factors (∑ŪĶM¶Ļģ… 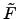 ¶≥•iĮŗ§£¨O F ™ļ finite
extension). §£ĻL•—©ů≥o≠”©w≤z™ļ√“©ķĽ›•ő®ž©“Ņ◊™ļ Zorn's Lemma,
ßŕ≠ŐīN≤§•h§£√“§F.
¶≥•iĮŗ§£¨O F ™ļ finite
extension). §£ĻL•—©ů≥o≠”©w≤z™ļ√“©ķĽ›•ő®ž©“Ņ◊™ļ Zorn's Lemma,
ßŕ≠ŐīN≤§•h§£√“§F.



§U§@≠∂: Finite Fields
§W§@≠∂: §§ĮŇ Field ™ļ© ĹŤ
ęe§@≠∂: Algebraic Closure
Administrator
2005-06-18
![]()
![]() •H§ő
q(x)
•H§ő
q(x) ![]() F[x] ®ŌĪo
f (x) = (x - a)k . q(x), ®š§§ q(a)
F[x] ®ŌĪo
f (x) = (x - a)k . q(x), ®š§§ q(a)![]() 0
(ßY x - a §£¨O q(x) ™ļ divisor). ßŕ≠Ő®Ő¶Ļ®”©włq a ¶b f (x)
™ļ≠ęģŕľ∆.
0
(ßY x - a §£¨O q(x) ™ļ divisor). ßŕ≠Ő®Ő¶Ļ®”©włq a ¶b f (x)
™ļ≠ęģŕľ∆.
![]() L ĽP F[x] §§™ļ polynomials ™ļ√ŲęY.
©“•Hßŕ≠Ő¶ŘĶM∑|į›: ĶĻ©w•Ű§@ęDĪ`ľ∆™ļ
f (x)
L ĽP F[x] §§™ļ polynomials ™ļ√ŲęY.
©“•Hßŕ≠Ő¶ŘĶM∑|į›: ĶĻ©w•Ű§@ęDĪ`ľ∆™ļ
f (x) ![]() F[x] ¨Oß_•i•Hßš®ž F
™ļ§@≠” extension L ®ŌĪo f (x) ¶b L §§¶≥ģŕ? Ķ™ģ◊¨O™÷©w™ļ.
•H§U™ļ©w≤zīN¨O¶^Ķ™≥o≠”į›√D. ßŕ≠ŐĪN∑|ęōļc§@≠” F ™ļ extension field
ĶMꊼ°©ķ¶b®š§§•ißš®ž§@≠”ģŕ. ≥o≠”©w≤z™ļ√“©ķ¶Pĺ«©ő≥|ńĪĪo``ĶÍĶÍ''™ļ,
¶]¨į¶nĻ≥®S¶≥Įu™ļ¶bßšģŕ™ļ∑PńĪ.
§£ĻL≥oīN¨Oľ∆嫶bĹÕ¶s¶b© ©“√Ų§Ŗ™ļ≠ę¬I,
ßŕ≠Ő•u≠n™ĺĻD™F¶Ť¶s¶b¶”§£•≤Įu•Ņßi∂DßA™F¶Ť¨O§įĽÚ.
F[x] ¨Oß_•i•Hßš®ž F
™ļ§@≠” extension L ®ŌĪo f (x) ¶b L §§¶≥ģŕ? Ķ™ģ◊¨O™÷©w™ļ.
•H§U™ļ©w≤zīN¨O¶^Ķ™≥o≠”į›√D. ßŕ≠ŐĪN∑|ęōļc§@≠” F ™ļ extension field
ĶMꊼ°©ķ¶b®š§§•ißš®ž§@≠”ģŕ. ≥o≠”©w≤z™ļ√“©ķ¶Pĺ«©ő≥|ńĪĪo``ĶÍĶÍ''™ļ,
¶]¨į¶nĻ≥®S¶≥Įu™ļ¶bßšģŕ™ļ∑PńĪ.
§£ĻL≥oīN¨Oľ∆嫶bĹÕ¶s¶b© ©“√Ų§Ŗ™ļ≠ę¬I,
ßŕ≠Ő•u≠n™ĺĻD™F¶Ť¶s¶b¶”§£•≤Įu•Ņßi∂DßA™F¶Ť¨O§įĽÚ.
![]() : F
: F![]() F[x]/
F[x]/![]() p(x)
p(x)![]() , ©włq¶®
, ©włq¶®
![]() (c) =
(c) = ![]() , ę‹ģe©ŲŇÁ√“
, ę‹ģe©ŲŇÁ√“ ![]() ¨O§@≠”
ring homomorphism. §]ę‹ģe©ŲŇÁ√“
¨O§@≠”
ring homomorphism. §]ę‹ģe©ŲŇÁ√“ ![]() ¨O§@ĻÔ§@™ļ: ≥o¨O¶]¨į¶p™G
c
¨O§@ĻÔ§@™ļ: ≥o¨O¶]¨į¶p™G
c ![]() ker(
ker(![]() ), ™Ū•‹
), ™Ū•‹
![]() =
= ![]() , ßY
c
, ßY
c ![]()
![]() p(x)
p(x)![]() . ¶ż¨O
. ¶ż¨O
![]() p(x)
p(x)![]() §§į£§F 0 •H• ®S¶≥®š•L™ļĪ`ľ∆, ¨GĪo c = 0 (§]•iģM•ő
Proposition 9.1.5 (2) Īo®ž
§§į£§F 0 •H• ®S¶≥®š•L™ļĪ`ľ∆, ¨GĪo c = 0 (§]•iģM•ő
Proposition 9.1.5 (2) Īo®ž ![]() ¨O§@ĻÔ§@). ¶]¶ĻĪo√“
im(
¨O§@ĻÔ§@). ¶]¶ĻĪo√“
im(![]() ) ¨O L ™ļ subfield •B©M F ¨O isomorphic ™ļ.
) ¨O L ™ļ subfield •B©M F ¨O isomorphic ™ļ.
![]()
![]() L,
ßŕ≠Ő≠nĽ°©ķ
p(
L,
ßŕ≠Ő≠nĽ°©ķ
p(![]() ) =
) = ![]() (™`∑N
(™`∑N
![]() ¨O
L = F[x]/
¨O
L = F[x]/![]() p(x)
p(x)![]() ™ļ 0). į≤≥]
p(x) = anxn + ... + a1x + a0, ®š§§ ai
™ļ 0). į≤≥]
p(x) = anxn + ... + a1x + a0, ®š§§ ai ![]() F. ®ļĽÚ
p(a) ∑|¨O§įĽÚ©O? ßOß—§Fßŕ≠Őī£ĻL≥ołŐ•N§J a •≤∂∑•ő®ž™ļ¨O L
§§™ļĻBļ‚, ¶”¶b L §§ c
F. ®ļĽÚ
p(a) ∑|¨O§įĽÚ©O? ßOß—§Fßŕ≠Őī£ĻL≥ołŐ•N§J a •≤∂∑•ő®ž™ļ¨O L
§§™ļĻBļ‚, ¶”¶b L §§ c ![]() F ¨OĽ›łgĻL
F ¨OĽ›łgĻL ![]() įe®ž L ™ļ,
īę•ył‹Ľ°ßŕ≠Ő•≤∂∑¶“ľ™ļ¨O
įe®ž L ™ļ,
īę•ył‹Ľ°ßŕ≠Ő•≤∂∑¶“ľ™ļ¨O
![]() . ¶]¶Ļ¶≥
. ¶]¶Ļ¶≥ ![]() p(x)
p(x)![]() ) = deg(p(x)).
) = deg(p(x)). ![]()
![]() L'.
¶Ļģ…ßŕ≠Ő≥qĪ`ļŔ f (x) splits into linear factors in L'.
L'.
¶Ļģ…ßŕ≠Ő≥qĪ`ļŔ f (x) splits into linear factors in L'.
![]() ®ŌĪo F[x] §§™ļ©“¶≥ polynomial ¶b
®ŌĪo F[x] §§™ļ©“¶≥ polynomial ¶b ![]() §§≥£•i•H splits into
linear factors (∑ŪĶM¶Ļģ…
§§≥£•i•H splits into
linear factors (∑ŪĶM¶Ļģ… ![]() ¶≥•iĮŗ§£¨O F ™ļ finite
extension). §£ĻL•—©ů≥o≠”©w≤z™ļ√“©ķĽ›•ő®ž©“Ņ◊™ļ Zorn's Lemma,
ßŕ≠ŐīN≤§•h§£√“§F.
¶≥•iĮŗ§£¨O F ™ļ finite
extension). §£ĻL•—©ů≥o≠”©w≤z™ļ√“©ķĽ›•ő®ž©“Ņ◊™ļ Zorn's Lemma,
ßŕ≠ŐīN≤§•h§£√“§F.