假如 L 是 n-th cyclotomic field, 則由 Theorem 4.1.4 知
L/![]() 是 Galois extension, 我們要探討
L/
是 Galois extension, 我們要探討
L/![]() 的 Galois group
Gal(L/
的 Galois group
Gal(L/![]() ) 為何. 首先注意所有 xn - 1 的根在乘法群之下形成一個
cyclic group of order n, 事實上若令
) 為何. 首先注意所有 xn - 1 的根在乘法群之下形成一個
cyclic group of order n, 事實上若令
![]() = cos(2
= cos(2![]() /n) + i sin(2
/n) + i sin(2![]() /n) 則知
/n) 則知 ![]() 是其 generator.
換言之若 Cn 是所有 xn - 1 的根所成的集合, 則
Cn = {
是其 generator.
換言之若 Cn 是所有 xn - 1 的根所成的集合, 則
Cn = {![]() | 1
| 1![]() t
t![]() n} . 因此我們知
L =
n} . 因此我們知
L = ![]() (
(![]() ).
).
現若
![]()
![]() Gal(L/
Gal(L/![]() ), 則
), 則
![]() (
(![]() )n =
)n = ![]() (
(![]() ) = 1, 故知
) = 1, 故知
![]() (
(![]() ) 仍為
xn - 1 的一個根. 另一方面若
) 仍為
xn - 1 的一個根. 另一方面若
![]() (
(![]() )m = 1, 表示
)m = 1, 表示
![]() (
(![]() ) = 1, 故由
) = 1, 故由 ![]() 是 1-1 知
是 1-1 知
![]() = 1. 但由於
= 1. 但由於
![]() 的 order 為 n, 得證 n | m. 也就是說
的 order 為 n, 得證 n | m. 也就是說
![]() (
(![]() ) 的 order 也是 n. 在 Cn 中 order 是 n
的元素, 我們稱之為 primitive n-th root of 1. 也就是說若
) 的 order 也是 n. 在 Cn 中 order 是 n
的元素, 我們稱之為 primitive n-th root of 1. 也就是說若
![]()
![]() Gal(L/
Gal(L/![]() ), 則
), 則
![]() (
(![]() ) 是一個 primitive n-th
root of 1.
) 是一個 primitive n-th
root of 1.
那麼 Cn 中有多少 primitive n-th root of 1 呢? 現若
![]() 是一個 primitive n-th root of 1, 則由於
是一個 primitive n-th root of 1, 則由於 ![]() 的 order 為
n/gcd(t, n) (參見大學基礎代數講義Proposition 2.3.3) 我們得知
gcd(t, n) = 1. 也就是說 primitive n-th root of 1 的個數就是 1
到 n 之間和 n 互質的整數個數. 這個數在整數論中我們用
的 order 為
n/gcd(t, n) (參見大學基礎代數講義Proposition 2.3.3) 我們得知
gcd(t, n) = 1. 也就是說 primitive n-th root of 1 的個數就是 1
到 n 之間和 n 互質的整數個數. 這個數在整數論中我們用 ![]() (n)
來表示, 其中
(n)
來表示, 其中 ![]() 我們稱之為 Euler
我們稱之為 Euler ![]() -function.
-function.
事實上 1 到 n 之間和 n 互質的整數在
![]() /n
/n![]() 中形成一個乘法群, 通常我們都用
(
中形成一個乘法群, 通常我們都用
(![]() /n
/n![]() )* 來表示. 千萬不要將
)* 來表示. 千萬不要將
![]() /n
/n![]() 和
(
和
(![]() /n
/n![]() )* 搞混. 要注意
)* 搞混. 要注意
![]() /n
/n![]() 是一個 order 為
n 的加法群, 而
(
是一個 order 為
n 的加法群, 而
(![]() /n
/n![]() )* 是一個 order 為
)* 是一個 order 為 ![]() (n)
的乘法群. 另外
(n)
的乘法群. 另外
![]() /n
/n![]() 是 cyclic group 但
(
是 cyclic group 但
(![]() /n
/n![]() )*
有可能不是 cyclic group, 不過當然仍是 abelian group. 例如
)*
有可能不是 cyclic group, 不過當然仍是 abelian group. 例如
![]() /12
/12![]() = {
= {![]() ,
,![]() ,...,
,...,![]() } 是一個 cyclic group
generated by
} 是一個 cyclic group
generated by
![]() . 但
. 但
要了解
Gal(L/![]() ) 首先就需要知道
[L :
) 首先就需要知道
[L : ![]() ] 為何, 由於
L =
] 為何, 由於
L = ![]() (
(![]() ), 所以我們要知道
), 所以我們要知道 ![]() over
over
![]() 的 minimal
polynomial 的 degree 為何. 前面已知若
的 minimal
polynomial 的 degree 為何. 前面已知若
![]()
![]() Gal(L/
Gal(L/![]() ), 則
), 則
![]() (
(![]() ) =
) = ![]() , 其中
1
, 其中
1![]() t
t![]() n 且滿足
gcd(t, n) = 1, 又由於
n 且滿足
gcd(t, n) = 1, 又由於
![]() (
(![]() ) 必為
) 必為 ![]() over
over
![]() 的
minimal polynomial 的一個根, 所以我們很自然會考慮以下的多項式:
的
minimal polynomial 的一個根, 所以我們很自然會考慮以下的多項式:
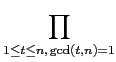 (x -
(x -
首先我們要證明
fn(x) ![]()
![]() [x], 再利用
[x], 再利用
![]() [x] 上的分解性質證明
fn(x) 是
[x] 上的分解性質證明
fn(x) 是
![]() [x] 中的 irreducible polynomial.
[x] 中的 irreducible polynomial.
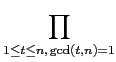 (x -
(x -
現在我們要證明
fn(x) ![]()
![]() [x]. 由於
xn - 1 =
[x]. 由於
xn - 1 = ![]() (x -
(x - ![]() ), 所以存在
g(x)
), 所以存在
g(x) ![]() L[x] 使得
xn - 1 = fn(x)g(x).
對任意
L[x] 使得
xn - 1 = fn(x)g(x).
對任意
![]()
![]() Gal(L/
Gal(L/![]() ), 將
), 將 ![]() 作用到兩邊多項式的係數,
得
xn - 1 = fn
作用到兩邊多項式的係數,
得
xn - 1 = fn![]() (x)g
(x)g![]() (x) = fn(x)g
(x) = fn(x)g![]() (x). 因此由
(x). 因此由
![]() [x] 上的唯一分解性質, 得知對任意
[x] 上的唯一分解性質, 得知對任意
![]()
![]() Gal(L/
Gal(L/![]() ) 皆有
g
) 皆有
g![]() (x) = g(x). 故知
g(x)
(x) = g(x). 故知
g(x) ![]()
![]() [x]. 現因為 fn(x) 和 g(x)
都是
[x]. 現因為 fn(x) 和 g(x)
都是
![]() [x] 中的 monic polynomial, 所以存在
c1, c2
[x] 中的 monic polynomial, 所以存在
c1, c2 ![]()
![]() 使得
c1fn(x), c2g(x)
使得
c1fn(x), c2g(x) ![]()
![]() [x] 且 c1fn(x) 和 c2g(x) 皆為
primitive polynomials (即各項係數的最大公因數為 1). 因此由
(c1fn(x))(c2g(x)) = c1c2(xn - 1)
[x] 且 c1fn(x) 和 c2g(x) 皆為
primitive polynomials (即各項係數的最大公因數為 1). 因此由
(c1fn(x))(c2g(x)) = c1c2(xn - 1) ![]()
![]() [x], 利用 Gauss Lemma
(參見大學基礎代數講義Lemma 7.3.5) 可得 c1c2 = 1, 故知
fn(x), g(x)
[x], 利用 Gauss Lemma
(參見大學基礎代數講義Lemma 7.3.5) 可得 c1c2 = 1, 故知
fn(x), g(x) ![]()
![]() [x]. 因此證得
fn(x)
[x]. 因此證得
fn(x) ![]()
![]() [x].
[x]. ![]()
接著我們要證明 fn(x) 在
![]() [x] 是 irreducible polynomial.
不過在證明之前我們需要一個滿技巧性的 Lemma. 首先介紹一下 notation.
若 p 是一個質數 且
a
[x] 是 irreducible polynomial.
不過在證明之前我們需要一個滿技巧性的 Lemma. 首先介紹一下 notation.
若 p 是一個質數 且
a ![]()
![]() , 則令
, 則令
![]() p =
p = ![]() /p
/p![]() 且
且
![]() 表示 a 在
表示 a 在
![]() p 中的值 (即 a modulo p). 同時若
f (x) = amxm + ... + a1x + a0
p 中的值 (即 a modulo p). 同時若
f (x) = amxm + ... + a1x + a0 ![]()
![]() [x], 則我們令
[x], 則我們令
![]() (x) =
(x) = ![]() xm + ... +
xm + ... + ![]() x +
x + ![]()
![]()
![]() p[x].
p[x].
回顧一下因為
![]() p 是一個 p 個元素的 finite field, 所以
p 是一個 p 個元素的 finite field, 所以
![]() p
的 characteristic 為 p 且對任意
a
p
的 characteristic 為 p 且對任意
a ![]()
![]() 皆有
皆有
![]() =
= ![]() .
因此若
l (x) = xm + am - 1xm - 1 + ... + a1x + a0, 則
.
因此若
l (x) = xm + am - 1xm - 1 + ... + a1x + a0, 則
| = | (xp)m + |
||
| = | (xm)p + |
||
| = | (xm + |
||
| = |
現在我們可以利用 Lemma 4.3.3 來證明 fn(x) 是
![]() [x] 中的
irreducible polynomial.
[x] 中的
irreducible polynomial.
現令 h(x) 為 ![]() over
over
![]() 的 minimal polynomial, 由於
fn(
的 minimal polynomial, 由於
fn(![]() ) = 0, 知 h(x) 在
) = 0, 知 h(x) 在
![]() [x] 中整除 fn(x). 但因為
fn(x) 是
[x] 中整除 fn(x). 但因為
fn(x) 是
![]() [x] 中的 monic polynomial, 由 Gauss Lemma 我們知
h(x)
[x] 中的 monic polynomial, 由 Gauss Lemma 我們知
h(x) ![]()
![]() [x] 且存在
l (x)
[x] 且存在
l (x) ![]()
![]() [x] 使得
fn(x) = h(x)l (x)
(參見大學基礎代數講義Lemma 7.3.8). 我們要證明若
1
[x] 使得
fn(x) = h(x)l (x)
(參見大學基礎代數講義Lemma 7.3.8). 我們要證明若
1![]() t
t![]() n 且
gcd(t, n) = 1, 則
h(
n 且
gcd(t, n) = 1, 則
h(![]() ) = 0.
) = 0.
假設 t 的質因數分解為
t = p1 ... pr (這裡 pi 未必相異),
由於
gcd(t, n) = 1, 我們知
pi![]() n. 由於
gcd(p1, n) = 1, 知
n. 由於
gcd(p1, n) = 1, 知
![]() 是一個 primitive n-th root of 1, 故知
fn(
是一個 primitive n-th root of 1, 故知
fn(![]() ) = 0, 但因為
h(
) = 0, 但因為
h(![]() ) = 0 且
) = 0 且
![]() (x) 在
(x) 在
![]() p1[x] 中是 separable polynomial, 由 Lemma 4.3.3 知
p1[x] 中是 separable polynomial, 由 Lemma 4.3.3 知
![]() 不可能是 l (x) 的一個根, 故得
h(
不可能是 l (x) 的一個根, 故得
h(![]() ) = 0.
同理由於
gcd(p2, n) = 1, 我們知
(
) = 0.
同理由於
gcd(p2, n) = 1, 我們知
(![]() )p2 也是
primitive n-th root of 1. 故由
fn((
)p2 也是
primitive n-th root of 1. 故由
fn((![]() )p2) = 0,
h(
)p2) = 0,
h(![]() ) = 0 以及
) = 0 以及
![]() (x) 在
(x) 在
![]() p2[x] 中是
separable polynomial, 再次利用 Lemma 4.3.3, 我們得知
h(
p2[x] 中是
separable polynomial, 再次利用 Lemma 4.3.3, 我們得知
h(![]() ) = 0. 因此用 induction, 我們知
h(
) = 0. 因此用 induction, 我們知
h(![]() ) = h(
) = h(![]() ) = 0.
) = 0.
我們證得了所有的 primitive n-th root of 1 都是 h(x) 的根,
而這些 primitive n-th root of 1 又剛好是 fn(x) 所有的根, 故由
h(x) 和 fn(x) 都是 monic polynomial 且 h(x) 整除 fn(x)
得證
h(x) = fn(x). 也就是說 fn(x) 是
![]() [x] 中的 irreducible
polynomial.
[x] 中的 irreducible
polynomial.
![]()
事實上在 Proposition 4.3.4 中我們證得了 fn(x) 就是
![]() over
over
![]() 的 minimal polynomial.
的 minimal polynomial.
現考慮函數
![]() : Gal(L/
: Gal(L/![]() )
)![]() (
(![]() /n
/n![]() )*, 其定義為: 若
)*, 其定義為: 若
![]()
![]() Gal(L/
Gal(L/![]() ), 且
), 且
![]() (
(![]() ) =
) = ![]() , 則定
, 則定
![]() (
(![]() ) =
) = ![]()
![]()
![]() /n
/n![]() . 首先檢查
. 首先檢查 ![]() 是一個
well-defined 函數. 假設
是一個
well-defined 函數. 假設
![]() (
(![]() ) =
) = ![]() 且
t'
且
t' ![]()
![]() 使得
使得
![]() =
= ![]() , 得
, 得
![]() = 1. 由於
= 1. 由於 ![]() 的 order 為 n, 故得
n | t - t', 也就是
的 order 為 n, 故得
n | t - t', 也就是
![]() -
- ![]() =
= ![]() =
= ![]() . 因此知
. 因此知
![]() =
= ![]() .
另一方面因為
.
另一方面因為
![]() (
(![]() ) 必為 primitive n-th root of 1,
故若
) 必為 primitive n-th root of 1,
故若
![]() (
(![]() ) =
) = ![]() , 則
gcd(t, n) = 1, 因此知
, 則
gcd(t, n) = 1, 因此知
![]() (
(![]() ) =
) = ![]()
![]() (
(![]() /n
/n![]() )*.
)*.
接下來檢查 ![]() 是一個 group homomorphism. 假設
是一個 group homomorphism. 假設
![]() ,
,![]()
![]() Gal(L/
Gal(L/![]() ) 且
) 且
![]() (
(![]() ) =
) = ![]() 以及
以及
![]() (
(![]() ) =
) = ![]() . 則
. 則
現假設
![]()
![]() ker(
ker(![]() ), 表示
), 表示
![]() (
(![]() ) =
) = ![]() . 現若
. 現若
![]() (
(![]() ) =
) = ![]() , 知
, 知
![]() (
(![]() ) =
) = ![]() =
= ![]() .
因而得知存在
m
.
因而得知存在
m ![]()
![]() 使得 t = mn + 1. 故知
使得 t = mn + 1. 故知
![]() (
(![]() ) =
) = ![]() =
= ![]() =
= ![]() . 也就是說
. 也就是說
![]() 是 L 到 L 的 identity. 得證
是 L 到 L 的 identity. 得證 ![]() 是 1-1. 最後由於
L/
是 1-1. 最後由於
L/![]() 是 Galois extension, 我們有
是 Galois extension, 我們有
![]() Gal(L/
Gal(L/![]() )
)![]() = [L :
= [L : ![]() ] =
] = ![]() (n) =
(n) = ![]() (
(![]() /n
/n![]() )*
)*![]() . 故由
. 故由
![]() : Gal(L/
: Gal(L/![]() )
)![]() (
(![]() /n
/n![]() )* 是 1-1 得證
)* 是 1-1 得證 ![]() 是 onto.
因此得證
Gal(L/
是 onto.
因此得證
Gal(L/![]() )
) ![]() (
(![]() /n
/n![]() )*.
)*.
![]()
當一個 field extension 是 Galois extension 且其 Galois group 是
abelian group 時, 我們稱此 extension 為 abelian extension.
Theorem 4.3.5 就是告訴我們當 L 是一個 cyclotomic field 時,
L/![]() 一定是一個 abelian extension. 特別當 p 是一個質數且 L 是
p-th cyclotomic field, 由於
一定是一個 abelian extension. 特別當 p 是一個質數且 L 是
p-th cyclotomic field, 由於
![]() /p
/p![]() 是 finite field 知
(
是 finite field 知
(![]() /p
/p![]() )* 是一個 cyclic group, 所以
L/
)* 是一個 cyclic group, 所以
L/![]() 是一個 cyclic
extension.
是一個 cyclic
extension.
一般來說當 L/K 是一個 abelian extension 且 [L : K] = m 時, 我們知
Gal(L/K) 是一個 order m 的 abelian group. 由 abelian group
的性質知, 對任意滿足 s | m 的正整數 s 皆存在一個 (不一定唯一)
subgroup
H ![]() Gal(L/K) 滿足
Gal(L/K) 滿足
![]() H
H![]() = s. 反之若 H 是
Gal(L/K) 的 subgroup, 由 Lagrange Theorem 知
= s. 反之若 H 是
Gal(L/K) 的 subgroup, 由 Lagrange Theorem 知
![]() H
H![]() | m.
另外因為
Gal(L/K) 是 abelian group, 所以
Gal(L/K) 的 subgroup
H 都是 normal subgroup, 而且 H 以及
Gal(L/K)/H 都是 abelian
groups. 綜合這些結果, 由 First Fundamental Theorem 4.1.5
我們知道對任意 s | m, 皆存在一個 L/K 的 intermediate field F
滿足 [L : F] = s, 而且我們知
Gal(L/F) 是一個 abelian group of order
s. 另外因為
Gal(L/F) 是
Gal(L/K) 的 normal subgroup, 所以由
Second Fundamental Theorem 4.1.8 知 F/K 也是 Galois
extension, 而且
Gal(F/K) isomorphic to
Gal(L/K)/Gal(L/F)
也是一個 abelian group. 這些結果都可套用到 L 是 cyclotomic field
且
K =
| m.
另外因為
Gal(L/K) 是 abelian group, 所以
Gal(L/K) 的 subgroup
H 都是 normal subgroup, 而且 H 以及
Gal(L/K)/H 都是 abelian
groups. 綜合這些結果, 由 First Fundamental Theorem 4.1.5
我們知道對任意 s | m, 皆存在一個 L/K 的 intermediate field F
滿足 [L : F] = s, 而且我們知
Gal(L/F) 是一個 abelian group of order
s. 另外因為
Gal(L/F) 是
Gal(L/K) 的 normal subgroup, 所以由
Second Fundamental Theorem 4.1.8 知 F/K 也是 Galois
extension, 而且
Gal(F/K) isomorphic to
Gal(L/K)/Gal(L/F)
也是一個 abelian group. 這些結果都可套用到 L 是 cyclotomic field
且
K = ![]() 的情形. 因此當 F 是
L/
的情形. 因此當 F 是
L/![]() 的 intermediate field 時,
我們得 L/F 以及
F/
的 intermediate field 時,
我們得 L/F 以及
F/![]() 都是 abelian extension.
都是 abelian extension.
我們知道了每一個 cyclotomic field 的 subfield 都是 finite abelian
extension over
![]() . 事實上反過來也是對的: 任意 finite abelian
extension over
. 事實上反過來也是對的: 任意 finite abelian
extension over
![]() 都會是某一個 cyclotomic field 的 subfield.
這就是所謂的 Kronecker-Weber Theorem.
當然了這個定理的證明超出了這個講義的範圍, 不過相信若你已熟悉了
Galois 理論, 要探索這些進階的理論已不是難事.
都會是某一個 cyclotomic field 的 subfield.
這就是所謂的 Kronecker-Weber Theorem.
當然了這個定理的證明超出了這個講義的範圍, 不過相信若你已熟悉了
Galois 理論, 要探索這些進階的理論已不是難事.