-
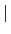 Gal(L/K)
Gal(L/K)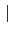 = [L : K]
= [L : K]
- Gal(L/K) 的 fixed field 是 K.
- L/K 是一個 normal and separable extension.
在一般代數書中對於 Galois extension 的定義不盡相同, 不過這些定義其實是等價的. 我們首先來探討這些等價關係.
(2) ![]() (3): 回顧
Gal(L/K) 的 fixed field 的定義為
{
(3): 回顧
Gal(L/K) 的 fixed field 的定義為
{![]()
![]() L |
L | ![]() (
(![]() ) =
) = ![]() ,
, ![]()
![]()
![]() Gal(L/K)}. 所以
K 為
Gal(L/K) 的 fixed field 不只是說 K 中的元素都會被所有的
Gal(L/K)}. 所以
K 為
Gal(L/K) 的 fixed field 不只是說 K 中的元素都會被所有的
![]()
![]() Gal(L/K) 固定, 也表示 L 中被所有的
Gal(L/K) 固定, 也表示 L 中被所有的
![]()
![]() Gal(L/K) 固定的元素必定落在 K 中. 現任取 a
Gal(L/K) 固定的元素必定落在 K 中. 現任取 a ![]() L,
假設 a over K 的 minimal polynomial 為 p(x). 令
a = a1, a2,..., an 為 p(x) 在 L 中所有的相異根. 考慮
f (x) = (x - a1)(x - a2) ... (x - an). 由於 n 為 p(x) 在 L
中相異根的個數, 因此我們知
deg(f (x)) = n
L,
假設 a over K 的 minimal polynomial 為 p(x). 令
a = a1, a2,..., an 為 p(x) 在 L 中所有的相異根. 考慮
f (x) = (x - a1)(x - a2) ... (x - an). 由於 n 為 p(x) 在 L
中相異根的個數, 因此我們知
deg(f (x)) = n![]() deg(p(x)). 又由於
a1, a2,..., an
deg(p(x)). 又由於
a1, a2,..., an ![]() L, 我們有
f (x)
L, 我們有
f (x) ![]() L[x]. 現假設
f (x) = xn + cn - 1xn - 1 + ... + c1x + c0, 其中 ci
L[x]. 現假設
f (x) = xn + cn - 1xn - 1 + ... + c1x + c0, 其中 ci ![]() L. 對任意
L. 對任意
![]()
![]() Gal(L/K), 我們有
Gal(L/K), 我們有
| f |
(3) ![]() (1): 假設 L/K 是一個 normal and separable
extension, 由 separable extension 的性質 (Theorem 3.4.5)
知若 N/K 是包含 L 的 finite normal extension, 則
(1): 假設 L/K 是一個 normal and separable
extension, 由 separable extension 的性質 (Theorem 3.4.5)
知若 N/K 是包含 L 的 finite normal extension, 則
![]()
![]()
![]() = [L : K]. 但由於 L/K 是 normal extension, 由 Lemma
3.2.6 知
Gal(L/K) =
= [L : K]. 但由於 L/K 是 normal extension, 由 Lemma
3.2.6 知
Gal(L/K) = ![]() , 得證
, 得證
![]() Gal(L/K)
Gal(L/K)![]() = [L : K].
= [L : K].
![]()
我們對符合以上任一項的 finite extension 稱之為 Galois extension.
要注意由於 F/K 不一定是 normal extension (參見 Example 3.2.4 (1)), 所以在 Proposition 4.1.3 中 F/K 不一定是 Galois extension.
在一般的情況如何檢查一個 extension 是否為 normal 和 separable extension 呢? 在 Theorem 3.2.2 和 Theorem 3.4.7, 我們分別介紹了檢查 normal extension 和 separable extension 的方法, 所以綜合這兩個定理, 我們得到了檢查 Galois extension 的方法.
(2) ![]() (1): 假設
b1,..., bm
(1): 假設
b1,..., bm ![]() L 是 f (x) 所有的根.
因為 L 是 f (x) over K 的 splitting field, 我們得
L = K(b1,..., bm). 由於 f (x) 是 separable polynomial, 每一個
bi over K 的 minimal polynomial 因為整除 f (x) 必也是
separable polynomial, 因此 bi 皆為 separable element over K.
故由 Theorem 3.4.7 知 L/K 是 separable extension. 又因為
L 是 f (x) over K 的 splitting field, 故由 Theorem 3.2.2
知 L/K 是 normal extension. 因此得 L/K 是 Galois extension.
L 是 f (x) 所有的根.
因為 L 是 f (x) over K 的 splitting field, 我們得
L = K(b1,..., bm). 由於 f (x) 是 separable polynomial, 每一個
bi over K 的 minimal polynomial 因為整除 f (x) 必也是
separable polynomial, 因此 bi 皆為 separable element over K.
故由 Theorem 3.4.7 知 L/K 是 separable extension. 又因為
L 是 f (x) over K 的 splitting field, 故由 Theorem 3.2.2
知 L/K 是 normal extension. 因此得 L/K 是 Galois extension.
![]()
我們曾經提過, Galois 理論就是要探討一個 extension 其 Galois group 的
subgroups 以及這個 extension 的 intermediate fields 之間的關係.
我們曾介紹過兩個函數來探討它們之間的關係, 現在回顧一下這兩個函數.
假設 L/K 是 finite extension. 我們定義
![]() 是 L/K 的
intermediate fields 所成的集合, 即
是 L/K 的
intermediate fields 所成的集合, 即
![]() . 且令
. 且令
![]() 是
Gal(L/K) 的 subgroups 所成的集合, 即
是
Gal(L/K) 的 subgroups 所成的集合, 即
![]() 我們定義函數
我們定義函數
![]() :
: ![]() 如下: 對任意 L/K 的 intermediate field F (即
F
如下: 對任意 L/K 的 intermediate field F (即
F ![]()
![]() ), 我們定義
), 我們定義
![]() (F) = Gal(L/F). 而函數
(F) = Gal(L/F). 而函數
![]() :
: ![]() 的定義為: 對任意
Gal(L/K) 的 subgroup H (即
H
的定義為: 對任意
Gal(L/K) 的 subgroup H (即
H ![]()
![]() ), 我們定義
), 我們定義
![]() (H) 為 H 的 fixed field, 即
(H) 為 H 的 fixed field, 即
![]() (H) = LH.
(H) = LH.
對於一般的 finite extension L/K, Corollary 2.3.6 告訴我們
![]() 是 1-1 的函數且
是 1-1 的函數且
![]() 是 onto 的函數. 當 L/K 是 Galois extension
時我們可得
是 onto 的函數. 當 L/K 是 Galois extension
時我們可得
![]() 是 onto 的(因此是 1-1 且 onto 的函數) 以及
是 onto 的(因此是 1-1 且 onto 的函數) 以及
![]() 是
1-1 的函數 (因此是 1-1 且 onto 的函數). 這就是所謂 Galois 理論的
fundamental theory. 這個 fundamental theory 事實上有兩部分,
我們將它們分開討論.
是
1-1 的函數 (因此是 1-1 且 onto 的函數). 這就是所謂 Galois 理論的
fundamental theory. 這個 fundamental theory 事實上有兩部分,
我們將它們分開討論.
接著要說明
![]() :
: ![]() , 給了
, 給了
![]() 到
到
![]() 之間一個一對一的對應關係. 注意這裡提的一對一對應關係 (one to one
correspondence) 指的是兩個集合間的對應關係, 也就是說
之間一個一對一的對應關係. 注意這裡提的一對一對應關係 (one to one
correspondence) 指的是兩個集合間的對應關係, 也就是說
![]() 中的每一個元素在
中的每一個元素在
![]() 中都可找到唯一的元素與之對應, 反之亦然.
因此我們不只要說明
中都可找到唯一的元素與之對應, 反之亦然.
因此我們不只要說明
![]() :
: ![]() 是 1-1 且要說明其為 onto. 現若
F1, F2
是 1-1 且要說明其為 onto. 現若
F1, F2 ![]()
![]() 滿足
滿足
![]() (F1) =
(F1) = ![]() (F2), 套用
(F2), 套用
![]() 於其上得
於其上得
![]() (
(![]() (F1)) =
(F1)) = ![]() (
(![]() (F2)). 故由
(F2)). 故由
![]() (
(![]() (F)) = F, 得知 F1 = F2.
另一方面任取
H
(F)) = F, 得知 F1 = F2.
另一方面任取
H ![]()
![]() , 考慮
F =
, 考慮
F = ![]() (H), 則由
(H), 則由
![]() (
(![]() (H)) = H
(Corollary 2.3.6) 知
(H)) = H
(Corollary 2.3.6) 知
![]() (F) = H. 故得知
(F) = H. 故得知
![]() :
: ![]() 確實給了
確實給了
![]() 和
和
![]() 兩個集合之間一個一對一的對應關係.
兩個集合之間一個一對一的對應關係.
![]()
當 L/K 是 finite Galois extension, 由 Corollary 2.3.6 以及
Theorem 4.1.5 我們知道對所有
H ![]()
![]() 以及
F
以及
F ![]()
![]() 皆有
皆有
![]() (
(![]() (H)) = H 以及
(H)) = H 以及
![]() (
(![]() (F)) = F. 也就是說此時
(F)) = F. 也就是說此時
![]() 和
和
![]() 互為反函數. 不過要注意若
F1, F2
互為反函數. 不過要注意若
F1, F2 ![]()
![]() 且
F1
且
F1 ![]() F2, 則
F2, 則
![]() (F2)
(F2) ![]()
![]() (F1) (Lemma 2.1.2). 也就是說較大的
intermediate field 對應到較小的 subgroup. 反之, 若
H1, H2
(F1) (Lemma 2.1.2). 也就是說較大的
intermediate field 對應到較小的 subgroup. 反之, 若
H1, H2 ![]()
![]() 且
H1
且
H1 ![]() H2, 則
H2, 則
![]() (H2)
(H2) ![]()
![]() (H1) (Lemma
2.2.2). 因此要注意較大的 subgroup 對應到較小的 intermediate
field. 這樣大小顛倒的對應關係也可由以下 extension degree 和 group
order 的關係看出.
(H1) (Lemma
2.2.2). 因此要注意較大的 subgroup 對應到較小的 intermediate
field. 這樣大小顛倒的對應關係也可由以下 extension degree 和 group
order 的關係看出.
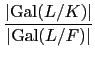 =
= 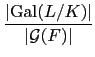 .
.
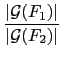 .
.
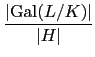 .
.
(2) 利用 Corollary 2.3.5 我們知
[![]() (H) : K] = [L : K]/
(H) : K] = [L : K]/![]() H
H![]() ,
故利用 L/K 是 Galois extension, 我們有
[
,
故利用 L/K 是 Galois extension, 我們有
[![]() (H) : K] =
(H) : K] = ![]() Gal(L/K)
Gal(L/K)![]() /
/![]() H
H![]() . 現若
H1
. 現若
H1 ![]() H2, 則
H2, 則
![]() (H2)
(H2) ![]()
![]() (H1), 故知
[
(H1), 故知
[![]() (H1) :
(H1) : ![]() (H2)] = [
(H2)] = [![]() (H1) : K]/[
(H1) : K]/[![]() (H2) : K] =
(H2) : K] = ![]() H2
H2![]() /
/![]() H1
H1![]() .
. ![]()
既然第一個 fundamental theorem 告訴我們 L/K 的 intermediate field 和 Gal(L/K) 的 subgroup 之間的對應關係. 所以我們很自然的會問到 Gal(L/K) 這個 group 的性質會不會影響到 L/K 的 intermediate field 的性質. 下一個 Lemma 就是告訴我們它們之間如何``互動''.
現假設
![]()
![]() Gal(L/
Gal(L/![]() (F)), 我們有
(F)), 我們有
![]() : L
: L![]() L 且對任意
L 且對任意
![]()
![]() F 皆有
F 皆有
![]() (
(![]() (
(![]() )) =
)) = ![]() (
(![]() ). 令
). 令
![]() =
= ![]() o
o![]() o
o![]() : L
: L![]() L. 因為
Gal(L/K)
是一個 group 且
L. 因為
Gal(L/K)
是一個 group 且
![]()
![]() Gal(L/
Gal(L/![]() (F))
(F)) ![]() Gal(L/K), 我們知
Gal(L/K), 我們知
![]()
![]() Gal(L/K). 又對於任意
Gal(L/K). 又對於任意
![]()
![]() F, 皆有
F, 皆有
反之, 若
![]()
![]()
![]() oGal(L/F)o
oGal(L/F)o![]() , 表示存在
, 表示存在
![]()
![]() Gal(L/F) 滿足
Gal(L/F) 滿足
![]() =
= ![]() o
o![]() o
o![]() . 因為
Gal(L/K) 是一個 group 且
. 因為
Gal(L/K) 是一個 group 且
![]()
![]() Gal(L/F)
Gal(L/F) ![]() Gal(L/K),
我們知
Gal(L/K),
我們知
![]()
![]() Gal(L/K). 然而對任意
Gal(L/K). 然而對任意
![]()
![]() F, 因為
F, 因為 ![]() 固定 F 中的元素, 所以
固定 F 中的元素, 所以
![]() (
(![]() ) =
) = ![]() . 因此對任意
. 因此對任意
![]()
![]() F 皆有
F 皆有
現若 F/K 是 Galois extension, 則依定義知 F/K 是 finite normal
extension. 對任意
![]()
![]() Gal(L/K), 由於
Gal(L/K), 由於
![]() |F : F
|F : F![]() L
是一個 F 到 L 的 K-monomorphism, 故由 Lemma 3.2.6 知
L
是一個 F 到 L 的 K-monomorphism, 故由 Lemma 3.2.6 知
![]() |F 是一個 F 到 F 的 K-monomorphism. 換句話說
|F 是一個 F 到 F 的 K-monomorphism. 換句話說
![]() (F) = F, 因此由 Lemma 4.1.7 知
(F) = F, 因此由 Lemma 4.1.7 知
反之, 若
Gal(L/F) 是
Gal(L/K) 的 normal subgroup, 表示對任意
![]()
![]() Gal(L/K) 皆有
Gal(L/F) =
Gal(L/K) 皆有
Gal(L/F) = ![]() oGal(L/F)o
oGal(L/F)o![]() . 故由 Lemma
4.1.7 知
Gal(L/F) = Gal(L/
. 故由 Lemma
4.1.7 知
Gal(L/F) = Gal(L/![]() (F)). 也就是說對任意
(F)). 也就是說對任意
![]()
![]() Gal(L/K) 皆有
Gal(L/K) 皆有
![]() (F) =
(F) = ![]() (
(![]() (F)). 由於 L/K 是
Galois extension, 故得
(F)). 由於 L/K 是
Galois extension, 故得
![]() :
: ![]() 是一對一的函數 (Theorem
4.1.5), 因此對任意
是一對一的函數 (Theorem
4.1.5), 因此對任意
![]()
![]() Gal(L/K) 皆有
Gal(L/K) 皆有
![]() (F) = F.
換言之, 對任意
(F) = F.
換言之, 對任意
![]()
![]() Gal(L/K), 皆有
Gal(L/K), 皆有
![]() |F : F
|F : F![]() F 是 F
到 F 的 K-monomorphism, 因此知
F 是 F
到 F 的 K-monomorphism, 因此知
![]() |F
|F ![]() Gal(F/K).
現考慮函數
Gal(F/K).
現考慮函數
![]() : Gal(L/K)
: Gal(L/K)![]() Gal(F/K), 使得對任意
Gal(F/K), 使得對任意
![]()
![]() Gal(L/K), 定義
Gal(L/K), 定義
![]() (
(![]() ) =
) = ![]() |F. 很容易得知
|F. 很容易得知
![]() 是一個 group homomorphism. 若
是一個 group homomorphism. 若
![]()
![]() Gal(F/K), 則由於
F
Gal(F/K), 則由於
F ![]() L 可將
L 可將 ![]() 視為 F 到 L 的 K-monomorphism.
又因為 L/K 是 normal extension, 故利用 Theorem 3.2.7
知存在
視為 F 到 L 的 K-monomorphism.
又因為 L/K 是 normal extension, 故利用 Theorem 3.2.7
知存在
![]()
![]() Gal(L/K) 使得
Gal(L/K) 使得
![]() |F =
|F = ![]() . 也就是說, 對任意
. 也就是說, 對任意
![]()
![]() Gal(F/K) 皆存在
Gal(F/K) 皆存在
![]()
![]() Gal(L/K) 使得
Gal(L/K) 使得
![]() (
(![]() ) =
) = ![]() . 證得
. 證得
![]() : Gal(L/K)
: Gal(L/K)![]() Gal(F/K) 是 onto.
接著我們要探討
ker(
Gal(F/K) 是 onto.
接著我們要探討
ker(![]() ) (即
) (即 ![]() 的 kernel) 為何. 若
的 kernel) 為何. 若
![]()
![]() ker(
ker(![]() ), 表示
), 表示
![]() (
(![]() ) =
) = ![]() |F 是
Gal(F/K)
的 identity. 亦即對任意
|F 是
Gal(F/K)
的 identity. 亦即對任意
![]()
![]() F 皆有
F 皆有
![]() (
(![]() ) =
) = ![]() |F(
|F(![]() ) =
) = ![]() . 因此知
. 因此知
![]() : L
: L![]() L
將 F 的元素固定, 也就是說
L
將 F 的元素固定, 也就是說
![]()
![]() Gal(L/F). 另一方面若
Gal(L/F). 另一方面若
![]()
![]() Gal(L/F), 則依定義
Gal(L/F), 則依定義 ![]() 將 F 的元素固定, 故知
將 F 的元素固定, 故知
![]() | F : F
| F : F![]() F 是 identity. 也就是說
F 是 identity. 也就是說
![]()
![]() ker(
ker(![]() ), 得證
ker(
), 得證
ker(![]() ) = Gal(L/F). 因此利用 group 的 first isomorphism 定理
(參見大學基礎代數講義Theorem 2.6.1) 得知:
) = Gal(L/F). 因此利用 group 的 first isomorphism 定理
(參見大學基礎代數講義Theorem 2.6.1) 得知:
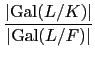 =
= ![$\displaystyle {\frac{[L:K]}{[L:F]}}$](img260.gif) =
= ![$\displaystyle {\frac{[L:F][F:K]}{[L:F]}}$](img261.gif) = [F : K].
= [F : K].
要注意 Theorem 4.1.8 事實上就是證明在 L/K 是 finite Galois
extension 的前提之下, F/K 是 normal extension 若且唯若
Gal(L/F) 是
Gal(L/K) 的 normal subgroup. 不過在 F/K 是
normal extension 推導得
Gal(L/F) 是
Gal(L/K) 的 normal
subgroup 的過程中我們僅需 L/K 是 normal extension 的假設 (即不需
L/K 是 separable extension). 不過由
Gal(L/F) 是
Gal(L/K) 的
normal subgroup 推導得 F/K 是 normal extension 的過程中我們需要
L/K 是 Galois extension 的假設 (即不只 L/K 是 normal extension
且需 L/K 是 separable extension). 比方說證明中我們用到了
![]() 是
1-1 的性質就需 L/K 是 Galois extension 才會對.
是
1-1 的性質就需 L/K 是 Galois extension 才會對.
我們已經介紹完了在大學代數中需了解的 Galois 理論. 如果你只想知道 Galois 理論是什麼, 那麼原則上讀到這裡已經達到了這個目的, 可以不必繼續研讀下去. 不過若沒有探討一些相關的應用或例子, 或許大家無法理解如何運用這些理論以及其重要性. 從歷史的角度來看, Galois 理論的應用最好的例子, 就是解決了一般多項式方程式的公式解問題以及一些尺規作圖問題. 不過談論這些例子需要再探討一些 Group Theory 的問題. 一來我們不想將討論的東西複雜化以致掩蓋了我們要探討 Galois 理論的目的; 二來這些例子的結論在更進階的代數理論中並沒有太多的用處. 因此我們選擇不去探討這些古典的問題, 而在接下來幾節中談論一些在探討更進階的代數理論時可能比較需要的應用與例子.