


下一頁: Galois Extension
上一頁: Normal Extension 和 Separable
前一頁: Separable Polynomial
目 錄
在這一節中我們介紹另一個重要的 extension, separable extension.
首先我們會發現幾乎在大學代數中談的 extension 都是 separable
extension, 然後我們會進一步討論 separable extension 重要的性質.
在前面我們提過當
L = K( ) 是 K 的 finite simple extension 時,
若
) 是 K 的 finite simple extension 時,
若  的 minimal polynomial 沒有重根時, 我們就可以由其 minimal
polynomial degree 確實知道有關 L 的 K-monomorphisms 的個數.
所以我們有以下之定義.
的 minimal polynomial 沒有重根時, 我們就可以由其 minimal
polynomial degree 確實知道有關 L 的 K-monomorphisms 的個數.
所以我們有以下之定義.
Definition 3.4.1
假設
L/
K 是一個 finite extension. 若
a  L
L 且
a over
K 的
minimal polynomial 是 separable polynomial, 則稱
a 是一個
separable element over
K. 如果
L 中所有元素皆為 separable
element over
K, 則稱
L/
K 是一個
separable extension.
要注意要談一個元素是否是一個 separable element, 仍必須說明是 over
哪一個 field. 有可能在
K  F 的情形, a 是一個 separable
element over F 但不是 separable over K. 不過反過來如果已知 a
是一個 separable element over K 那麼 a 一定是一個 separable
element over F. 這是因為如果
mK(x)
F 的情形, a 是一個 separable
element over F 但不是 separable over K. 不過反過來如果已知 a
是一個 separable element over K 那麼 a 一定是一個 separable
element over F. 這是因為如果
mK(x)  K[x] 和
mF(x)
K[x] 和
mF(x)  F[x]
分別為 a over K 的 minimal polynomial 和 a over F 的 minimal
polynomial, 則 mF(x) 在 F[x] 中必整除 mK(x). 因此如果
mK(x) 沒有重根, 當然 mF(x) 也不會有重根.
F[x]
分別為 a over K 的 minimal polynomial 和 a over F 的 minimal
polynomial, 則 mF(x) 在 F[x] 中必整除 mK(x). 因此如果
mK(x) 沒有重根, 當然 mF(x) 也不會有重根.
當 L/K 是一個 finite extension, 前面提過我們很關心一些 L/K
的性質是否在 intermediate fields 之間保持. 事實上 separable
extension 和 algebraic extension 一樣是會被保持的.
Lemma 3.4.2
假設
L/
K 是一個 finite separable extension 且
F 是
L/
K 的
intermediate field. 則
L/
F 和
F/
K 都是 separable extension.
証 明.
任取
a  F
F, 由於
a  L
L 且
L/
K 是 separable extension, 得知
a 是一個 separable element over
K. 因此由定義知
F/
K 是
separable extension. 另外任取
a  L
L, 由於
K  F
F 且
a
是一個 separable element over
K, 由前面討論知
a 也是一個
separable element over
F. 因此知
L/
F 也是一個 separable
extension.
事實上以後我們會知道如果 L/F 和 F/K 都是 separable extension 則
L/K 也會是一個 separable extension (再一次強調 normal extension
就沒有這麼好).
要檢查 L/K 是否為 separable extension, 依定義就得檢查 L
中所有元素是否為 separable element over K.
我們自然希望有一個等價但比較容易檢查的條件 (就像前面提的 normal
extension). 以後等我們了解更多 separable extension 的性質之後,
我們會發現和 normal extension (Theorem 3.2.2) 一樣
只要檢查有限多個元素就可以了. 不過事實上在目前大學代數大家所熟悉的
field extension 都是 separable extension.
Proposition 3.4.3
假設
K 是一個 field. 則在以下兩個狀況之下的 finite extension 都是
separable extension.
- 當 K 的 characteristic 是 0 時;
- 當 K 是 finite field 時.
証 明.
(1) 當
K 的 characteristic 是 0 時, 由 Proposition
3.3.7
我們知所有
K[
x] 中的 irreducible polynomial 皆為 separable
polynomial. 若
L/
K 是 finite extension, 因為任意
a  L
L over
K
的 minimal polynomial 都是
K[
x] 中的 irreducible polynomial, 故得
a 皆為 separable element over
K. 得證
L/
K 是 separable
extension.
(2) 當 K 是 finite field 時, 首先我們複習一下 finite field 的性質.
我們知道 K 的 characteristic 必為一質數 p (參見大學基礎代數講義Lemma
9.2.3) 且 K 中元素個數必為 pn, 其中
n 
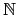 (參見大學基礎代數講義
Theorem 10.4.1). 由於
K
(參見大學基礎代數講義
Theorem 10.4.1). 由於
K 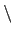 {0} 共有 pn - 1
個元素且在乘法之下是一個 group, 因此利用 Lagrange Theorem
我們知對任意 a
{0} 共有 pn - 1
個元素且在乘法之下是一個 group, 因此利用 Lagrange Theorem
我們知對任意 a  K 且 a
K 且 a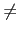 0 皆有
apn - 1 = 1. 兩邊各乘上
a, 得 K 中任意元素 a 皆滿足 apn = a. 因此若令
b = apn - 1, 則
bp = (apn - 1)p = apn = a. 換言之, 對任意
a
0 皆有
apn - 1 = 1. 兩邊各乘上
a, 得 K 中任意元素 a 皆滿足 apn = a. 因此若令
b = apn - 1, 則
bp = (apn - 1)p = apn = a. 換言之, 對任意
a  K, 皆存在 b
K, 皆存在 b  K 使得 bp = a. 另外由於 K 的
characteristic 為 p, 當 a, b
K 使得 bp = a. 另外由於 K 的
characteristic 為 p, 當 a, b  K 時我們有
(a + b)p = ap + bp
(參見大學基礎代數講義Lemma 9.2.5). 因此若
f (x) =
K 時我們有
(a + b)p = ap + bp
(參見大學基礎代數講義Lemma 9.2.5). 因此若
f (x) = 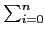 aixi, 則
f (x)p =
aixi, 則
f (x)p = 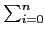 aipxip (參見大學基礎代數講義Lemma 9.2.6).
aipxip (參見大學基礎代數講義Lemma 9.2.6).
現假設 L/K 是一個 finite extension, 且假設存在 a  L 不是一個
separable element over K. 換言之, 若 a over K 的 minimal
polynomial 為 f (x), 則
f (x)
L 不是一個
separable element over K. 換言之, 若 a over K 的 minimal
polynomial 為 f (x), 則
f (x)  K[x] 不是一個 separable
polynomial. 因此由 Proposition 3.3.7 (2) 我們知存在
g(x) =
K[x] 不是一個 separable
polynomial. 因此由 Proposition 3.3.7 (2) 我們知存在
g(x) = 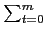 atxt
atxt  K[x] 使得
f (x) = g(xp). 由前面討論知,
對任意
t
K[x] 使得
f (x) = g(xp). 由前面討論知,
對任意
t  {0, 1,..., m} 皆存在 bt
{0, 1,..., m} 皆存在 bt  K 使得 btp = at.
因此
K 使得 btp = at.
因此
f (
x) =
g(
xp) =
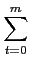 at
at(
xp)
t =
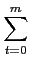 btp
btp(
xt)
p = (
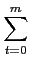 btxt
btxt)
p.
換言之, 若令
h(
x) =
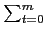 btxt
btxt  K
K[
x], 則
f (
x) =
h(
x)
p.
這和
f (
x) 在
K[
x] 中是 irreducible polynomial 相矛盾, 因此
L
中每個元素皆為 separable element over
K. 得證
L/
K 是 separable
extension.
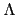
由此結果我們知, 以後若是談論
 的 finite extension 或是 finite
field 的 finite extension, 我們都可以直接說是 separable extension.
雖然 Proposition 3.4.3 幾乎涵蓋了我們常見的 extension,
但並沒有涵蓋所有的情形. 接下來我們簡單的介紹一個 finite extension
但不是 separable extension 的例子.
的 finite extension 或是 finite
field 的 finite extension, 我們都可以直接說是 separable extension.
雖然 Proposition 3.4.3 幾乎涵蓋了我們常見的 extension,
但並沒有涵蓋所有的情形. 接下來我們簡單的介紹一個 finite extension
但不是 separable extension 的例子.
Example 3.4.4
令
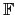 2
2 為一個只有兩個元素的 finite field,

是
transcendental over
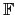 2
2 且令
K =
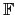 2
2(

). 要注意
K
雖然不再是 finite field 但是其 characteristic 仍為 2. 考慮
x2 -

 K
K[
x], 而令
L =
K(
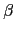
) 是
x2 -

over
K 的
splitting field, 其中
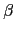
滿足
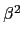
=

. 首先觀察
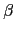
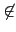 K
K. 這是因為若
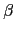
 K
K, 即表示存在
f (
x),
g(
x)

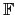 2
2[
x], 其中
g(
x)
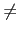
0 使得
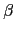
=
f (

)/
g(

).
換言之,
f (

)
2/
g(

)
2 =

. 這會造成

是
f (
x)
2 -
x . g(
x)
2 
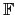 2
2[
x] 的一個根, 和

是
transcendental over
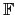 2
2 相矛盾. 故知
x2 -

是
K[
x] 中的
irreducible polynomial. 又因若令
h(
x) =
x -

, 則
x2 -

=
h(
x2), 故由 Proposition
3.3.7 知
x2 -

不是 separable polynomial. 因此
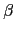
不是一個 separable element
over
K, 進而得知
L =
K(
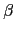
) 不是一個 separable extension over
K.
大家應該不難將這個例子推廣到一般 characteristic p 的例子.
接下來我們就來看看當初要介紹 separable extension 最主要的原因.
這也是有關 separable extension 最重要的性質.
Theorem 3.4.5
假設
L/
K 是一個 finite extension 且
N 是一個
L 的 extension
滿足
N/
K 是 finite normal extension. 則
L/
K 是一個 separable
extension 若且唯若
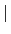
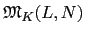
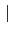
= [
L :
K].
証 明.
首先我們用類似 Proposition
3.2.13 的證明方法對 [
L :
K] 作
induction, 證明若
L/
K 是一個 finite separable extension 且
N
是一個
L 的 extension 滿足
N/
K 是 finite normal extension, 則
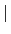
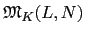
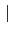
= [
L :
K]. 當 [
L :
K] = 1 時, 因為
L 到
N 的
K-monomorphism 只有 identity, 所以自然成立. 假設對所有 extension
degree 小於
n 的 separable extensions 皆成立. 現考慮 [
L :
K] =
n > 1
的情形. 任取

 L
L 但

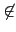 K
K. 令
F =
K(

),
此時我們有 [
F :
K] > 1 故知 [
L :
F] <
n. 假設
p(
x)
 K
K[
x] 是

over
K 的 minimal polynomial. 由於

 L
L 且
L/
K 是
separable extension, 所以

是一個 separable element over
K, 也就是說
p(
x) 是一個 separable polynomial. 然而
N/
K 是
normal extension, 故
p(
x) 在
N 中完全分解, 再加上
p(
x)
沒有重根, 故得
p(
x) 在
N 中的根的個數等於
deg(
p(
x)) = [
F :
K].
因此利用所有
K(

) 到
N 的
K-monomorphisms 的個數等於
p(
x) 在
N 中根的個數, 得知
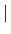
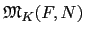
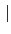
= [
F :
K].
另一方面因為 [
L :
F] <
n,
N/
F 是 normal extension (Corollary
3.2.3) 且
L/
F 是 separable extension (Lemma
3.4.2),
故套用 induction 的假設知
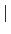
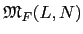
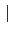
= [
L :
F]. 因此利用 Lemma
3.2.12 得知
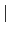
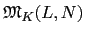
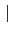
=
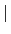
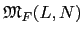
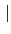
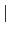
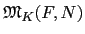
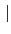
= [
L :
F][
F :
K] = [
L :
K].
反之, 如果 L/K 不是 separable extension, 由定義知存在
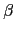
 L
不是 separable element over K. 換言之, 若
L
不是 separable element over K. 換言之, 若 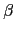 over K 的
minimal polynomial 為 h(x), 則 h(x) 在 N 中有重根.
因此若令
F = K(
over K 的
minimal polynomial 為 h(x), 則 h(x) 在 N 中有重根.
因此若令
F = K(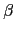 ) 則
) 則
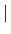
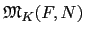
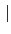 < deg(h(x)) = [F : K].
另一方面由 Proposition 3.2.13 我們知
< deg(h(x)) = [F : K].
另一方面由 Proposition 3.2.13 我們知
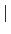
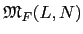
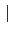
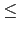 [L : F]. 故套用 Lemma 3.2.12 得知
[L : F]. 故套用 Lemma 3.2.12 得知
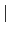
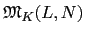
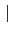
=
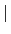
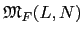
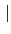
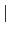
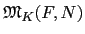
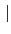
< [
L :
F][
F :
K] = [
L :
K].
利用 Theorem 3.4.5 我們便可以回答當初談到 Lemma 3.4.2
的反向為何也是對的.
Proposition 3.4.6
假設
L/
K 是一個 finite extension 且
F 是
L/
K 的 intermediate
field. 則
L/
K 是 separable extension 若且唯若
L/
F 和
F/
K 都是
separable extension.
証 明.
在 Lemma
3.4.2 中我們已證得若
L/
K 是 separable extension 則
L/
F 和
F/
K 都是 separable extension.
至於另一方向, 首先令 N 為 L/K 的 normal closure. 我們得 N 是
L 的一個 extension 且 N/K 以及 N/F 是 finite normal
extensions. 因此若 L/F 和 F/K 是 separable extensions, 則利用
Theorem 3.4.5 知
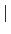
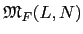
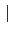 = [L : F] 且
= [L : F] 且
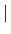
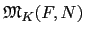
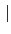 = [F : K]. 故利用 Lemma 3.2.12 得到
= [F : K]. 故利用 Lemma 3.2.12 得到
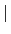
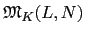
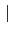 = [L : F][F : K] = [L : K]. 因此再次利用 Theorem
3.4.5 得知 L/K 是 separable extension.
= [L : F][F : K] = [L : K]. 因此再次利用 Theorem
3.4.5 得知 L/K 是 separable extension.
最後我們得到一個判別 separable extension 的好方法.
Theorem 3.4.7
假設
L/
K 是一個 field extension. 下列敘述是等價的.
- L/K 是 finite separable extension.
-
L = K(a1,..., am), 其中
a1,..., am 皆為 algebraic 且 separable element over
K.
証 明.
(1)
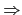
(2) 由於
L/
K 是 finite extension, 由 Proposition
1.3.4 知存在
a1,...,
am 是 algebraic over
K 使得
L =
K(
a1,...,
am). 又因為
L/
K 是 separable extension, 所有
L
中的元素都是 separable element over
K, 故知
ai 皆為 separable
element over
K.
(2) 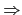 (1) 因為
a1,..., am 皆為 algebraic over K,
所以
L = K(a1,..., am) 是 finite extension over K. 我們對
[L : K] 作 induction. 假設 [L : K] = 1, 此時 L = K 所以 L/K 當然是
separable extension. 假設對於所有 degree 小於 n 的 extension
皆成立. 現若 [L : K] = n > 1, 故存在 ai 滿足
ai
(1) 因為
a1,..., am 皆為 algebraic over K,
所以
L = K(a1,..., am) 是 finite extension over K. 我們對
[L : K] 作 induction. 假設 [L : K] = 1, 此時 L = K 所以 L/K 當然是
separable extension. 假設對於所有 degree 小於 n 的 extension
皆成立. 現若 [L : K] = n > 1, 故存在 ai 滿足
ai 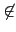 K.
不失一般性我們假設
a1
K.
不失一般性我們假設
a1 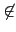 K. 令 F = K(a1), 則由於 [F : K] > 1,
我們有 [L : F] < n. 因為 a1 是 separable element over K, 所以
a1 over K 的 minimal polynomial p(x) 為 separable polynomial.
若令 N 為 L/K 的 normal closure, 我們得所有 F 到 N 的
K-monomorphisms 的個數等於
deg(p(x)) = [F : K]. 因此由 Theorem
3.4.5 知 F/K 是 finite separable extension. 另一方面由於
L = K(a1, a2,..., am) = K(a1)(a2,..., am) = F(a2,..., am) 且
a2,..., am 皆為 separable element over K, 當然也都是
separable element over F (因為
K
K. 令 F = K(a1), 則由於 [F : K] > 1,
我們有 [L : F] < n. 因為 a1 是 separable element over K, 所以
a1 over K 的 minimal polynomial p(x) 為 separable polynomial.
若令 N 為 L/K 的 normal closure, 我們得所有 F 到 N 的
K-monomorphisms 的個數等於
deg(p(x)) = [F : K]. 因此由 Theorem
3.4.5 知 F/K 是 finite separable extension. 另一方面由於
L = K(a1, a2,..., am) = K(a1)(a2,..., am) = F(a2,..., am) 且
a2,..., am 皆為 separable element over K, 當然也都是
separable element over F (因為
K  F), 故由 [L : F] < n
套用 induction 的假設知 L/F 是 finite separable extension.
因此利用 Proposition 3.4.6, 由 F/K 是 finite separable
extension 以及 L/F 是 finite separable extension 得知 L/K 是一個
finite separable extension.
F), 故由 [L : F] < n
套用 induction 的假設知 L/F 是 finite separable extension.
因此利用 Proposition 3.4.6, 由 F/K 是 finite separable
extension 以及 L/F 是 finite separable extension 得知 L/K 是一個
finite separable extension.
簡單來說 Theorem 3.4.7 告訴我們只要加入的元素都是 separable
element 那麼所得的 extension 就是 separable extension.
因此只要檢查加入的元素而不必檢查所有的元素.
最後我們要說明一點. 由於在這裡我們只談 finite extension,
所以我們只討論在 finite extension 之下的 normal extension 和 separable
extension. 事實上 normal extension 和 separable extension
的性質在一般的 algebraic extension 中也都可以討論.



下一頁: Galois Extension
上一頁: Normal Extension 和 Separable
前一頁: Separable Polynomial
目 錄
Li
2006-05-18
![]() ) 是 K 的 finite simple extension 時,
若
) 是 K 的 finite simple extension 時,
若 ![]() 的 minimal polynomial 沒有重根時, 我們就可以由其 minimal
polynomial degree 確實知道有關 L 的 K-monomorphisms 的個數.
所以我們有以下之定義.
的 minimal polynomial 沒有重根時, 我們就可以由其 minimal
polynomial degree 確實知道有關 L 的 K-monomorphisms 的個數.
所以我們有以下之定義.
![]()
![]() (參見大學基礎代數講義
Theorem 10.4.1). 由於
K
(參見大學基礎代數講義
Theorem 10.4.1). 由於
K ![]() {0} 共有 pn - 1
個元素且在乘法之下是一個 group, 因此利用 Lagrange Theorem
我們知對任意 a
{0} 共有 pn - 1
個元素且在乘法之下是一個 group, 因此利用 Lagrange Theorem
我們知對任意 a ![]() K 且 a
K 且 a![]() 0 皆有
apn - 1 = 1. 兩邊各乘上
a, 得 K 中任意元素 a 皆滿足 apn = a. 因此若令
b = apn - 1, 則
bp = (apn - 1)p = apn = a. 換言之, 對任意
a
0 皆有
apn - 1 = 1. 兩邊各乘上
a, 得 K 中任意元素 a 皆滿足 apn = a. 因此若令
b = apn - 1, 則
bp = (apn - 1)p = apn = a. 換言之, 對任意
a ![]() K, 皆存在 b
K, 皆存在 b ![]() K 使得 bp = a. 另外由於 K 的
characteristic 為 p, 當 a, b
K 使得 bp = a. 另外由於 K 的
characteristic 為 p, 當 a, b ![]() K 時我們有
(a + b)p = ap + bp
(參見大學基礎代數講義Lemma 9.2.5). 因此若
f (x) =
K 時我們有
(a + b)p = ap + bp
(參見大學基礎代數講義Lemma 9.2.5). 因此若
f (x) = ![]() aixi, 則
f (x)p =
aixi, 則
f (x)p = ![]() aipxip (參見大學基礎代數講義Lemma 9.2.6).
aipxip (參見大學基礎代數講義Lemma 9.2.6).
![]() L 不是一個
separable element over K. 換言之, 若 a over K 的 minimal
polynomial 為 f (x), 則
f (x)
L 不是一個
separable element over K. 換言之, 若 a over K 的 minimal
polynomial 為 f (x), 則
f (x) ![]() K[x] 不是一個 separable
polynomial. 因此由 Proposition 3.3.7 (2) 我們知存在
g(x) =
K[x] 不是一個 separable
polynomial. 因此由 Proposition 3.3.7 (2) 我們知存在
g(x) = ![]() atxt
atxt ![]() K[x] 使得
f (x) = g(xp). 由前面討論知,
對任意
t
K[x] 使得
f (x) = g(xp). 由前面討論知,
對任意
t ![]() {0, 1,..., m} 皆存在 bt
{0, 1,..., m} 皆存在 bt ![]() K 使得 btp = at.
因此
K 使得 btp = at.
因此
![]()
![]() L
不是 separable element over K. 換言之, 若
L
不是 separable element over K. 換言之, 若 ![]() over K 的
minimal polynomial 為 h(x), 則 h(x) 在 N 中有重根.
因此若令
F = K(
over K 的
minimal polynomial 為 h(x), 則 h(x) 在 N 中有重根.
因此若令
F = K(![]() ) 則
) 則
![]()
![]()
![]() < deg(h(x)) = [F : K].
另一方面由 Proposition 3.2.13 我們知
< deg(h(x)) = [F : K].
另一方面由 Proposition 3.2.13 我們知
![]()
![]()
![]()
![]() [L : F]. 故套用 Lemma 3.2.12 得知
[L : F]. 故套用 Lemma 3.2.12 得知
![]()
![]()
![]() = [L : F] 且
= [L : F] 且
![]()
![]()
![]() = [F : K]. 故利用 Lemma 3.2.12 得到
= [F : K]. 故利用 Lemma 3.2.12 得到
![]()
![]()
![]() = [L : F][F : K] = [L : K]. 因此再次利用 Theorem
3.4.5 得知 L/K 是 separable extension.
= [L : F][F : K] = [L : K]. 因此再次利用 Theorem
3.4.5 得知 L/K 是 separable extension.
![]()
![]() (1) 因為
a1,..., am 皆為 algebraic over K,
所以
L = K(a1,..., am) 是 finite extension over K. 我們對
[L : K] 作 induction. 假設 [L : K] = 1, 此時 L = K 所以 L/K 當然是
separable extension. 假設對於所有 degree 小於 n 的 extension
皆成立. 現若 [L : K] = n > 1, 故存在 ai 滿足
ai
(1) 因為
a1,..., am 皆為 algebraic over K,
所以
L = K(a1,..., am) 是 finite extension over K. 我們對
[L : K] 作 induction. 假設 [L : K] = 1, 此時 L = K 所以 L/K 當然是
separable extension. 假設對於所有 degree 小於 n 的 extension
皆成立. 現若 [L : K] = n > 1, 故存在 ai 滿足
ai ![]() K.
不失一般性我們假設
a1
K.
不失一般性我們假設
a1 ![]() K. 令 F = K(a1), 則由於 [F : K] > 1,
我們有 [L : F] < n. 因為 a1 是 separable element over K, 所以
a1 over K 的 minimal polynomial p(x) 為 separable polynomial.
若令 N 為 L/K 的 normal closure, 我們得所有 F 到 N 的
K-monomorphisms 的個數等於
deg(p(x)) = [F : K]. 因此由 Theorem
3.4.5 知 F/K 是 finite separable extension. 另一方面由於
L = K(a1, a2,..., am) = K(a1)(a2,..., am) = F(a2,..., am) 且
a2,..., am 皆為 separable element over K, 當然也都是
separable element over F (因為
K
K. 令 F = K(a1), 則由於 [F : K] > 1,
我們有 [L : F] < n. 因為 a1 是 separable element over K, 所以
a1 over K 的 minimal polynomial p(x) 為 separable polynomial.
若令 N 為 L/K 的 normal closure, 我們得所有 F 到 N 的
K-monomorphisms 的個數等於
deg(p(x)) = [F : K]. 因此由 Theorem
3.4.5 知 F/K 是 finite separable extension. 另一方面由於
L = K(a1, a2,..., am) = K(a1)(a2,..., am) = F(a2,..., am) 且
a2,..., am 皆為 separable element over K, 當然也都是
separable element over F (因為
K ![]() F), 故由 [L : F] < n
套用 induction 的假設知 L/F 是 finite separable extension.
因此利用 Proposition 3.4.6, 由 F/K 是 finite separable
extension 以及 L/F 是 finite separable extension 得知 L/K 是一個
finite separable extension.
F), 故由 [L : F] < n
套用 induction 的假設知 L/F 是 finite separable extension.
因此利用 Proposition 3.4.6, 由 F/K 是 finite separable
extension 以及 L/F 是 finite separable extension 得知 L/K 是一個
finite separable extension.
![]()