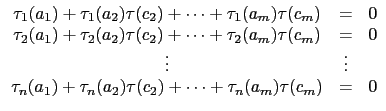


下一頁: Normal Extension 和 Separable
上一頁: Galois Group 和 Fixed
前一頁: Fixed Field
目 錄
當 L/K 是 finite extension 時
Gal(L/K) 會是一個 finite group
而且
Gal(L/K) 的 order 和 L/K 的 degree 相關.
這一節中我們就是要探討
 Gal(L/K)
Gal(L/K) 和 [L : K] 的關係.
和 [L : K] 的關係.
在 Corollary 2.1.4 中我們知道當 L/K 是 finite simple
extension 時,
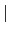 Gal(L/K)
Gal(L/K)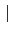
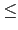 [L : K]. 所以知道在這情形時
Gal(L/K) 是一個 finite group. 事實上不需 simple 的假設, 當 L/K
是 finite extension 時
Gal(L/K) 必是一個 finite group.
[L : K]. 所以知道在這情形時
Gal(L/K) 是一個 finite group. 事實上不需 simple 的假設, 當 L/K
是 finite extension 時
Gal(L/K) 必是一個 finite group.
Lemma 2.3.1
若
L/
K 是一個 finite extension, 則
Gal(
L/
K) 是一個 finite
group.
証 明.
利用 Proposition
1.3.4, 我們知存在
a1,...,
an  L
L,
其中這些
ai 皆 algebraic over
K, 使得
L =
K(
a1,...,
an). 由
Lemma
1.3.5, 我們知對任意

 L
L, 皆存在
f (
x1,...,
xn)
 K
K[
x1,...,
xn] 使得

=
f (
a1,...,
an). 因此若
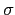

Gal(
L/
K), 則由於
f (
x1,...,
xn) 的係數都在
K 中, 可得
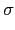
(
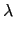
) =
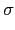
(
f (
a1,...,
an)) =
f (
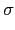
(
a1),...,
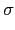
(
an)).
也就是說
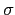
對
L 中元素的取值完全可由
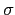
(
a1),...,
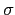
(
an) 來決定. 換句話說若
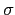
,
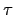

Gal(
L/
K) 且對於所有的
i = 1,...,
n, 皆有
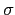
(
ai) =
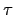
(
ai), 則
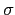
=
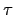
.
當
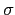
 Gal(L/K) 時,
Gal(L/K) 時,
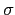 (ai) 有哪些可能的取值呢? 若
fi(x)
(ai) 有哪些可能的取值呢? 若
fi(x)  K[x] 是 ai over K 的 minimal polynomial, 且
deg(fi(x)) = mi, 則由於
K[x] 是 ai over K 的 minimal polynomial, 且
deg(fi(x)) = mi, 則由於
fi(
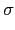
(
ai)) =
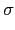
(
fi(
ai)) =
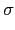
(0) = 0,
我們知
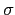
(
ai)
仍為
fi(
x) 在
L 中的一個根. 因此每個
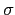
(
ai) 最多只有
mi 個選擇. 所以對任何
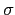

Gal(
L/
K) 這些
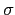
(
a1),...,
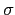
(
an) 最多有
m1 ... mn 種選擇, 故知
Gal(
L/
K) 最多只能有
m1 ... mn 個元素.
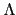
要注意如果 fi(x) 在 L 中有 si 個根, 並不能像 simple
extension 的情況得到
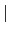 Gal(L/K)
Gal(L/K)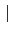 = s1 ... sn.
這是因為任意給定
= s1 ... sn.
這是因為任意給定
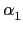 ,...,
,...,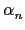
 L 分別為
f1(x) = 0,..., fn(x) 在 L 的根, 並不能保證存在
L 分別為
f1(x) = 0,..., fn(x) 在 L 的根, 並不能保證存在
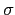
 Gal(L/K) 會同時滿足
Gal(L/K) 會同時滿足
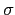 (a1) =
(a1) = 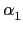 ,...,
,...,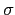 (an) =
(an) = 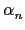 .
.
利用 Corollary 2.1.4 以及 induction 我們可以推導出, 若
L/K 是 finite extension, 則
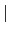 Gal(L/K)
Gal(L/K)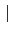
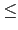 [L : K]. 例如若
L = K(a1, a2), 我們令 F = K(a1), 則知 L = F(a2). 因此由 L/F 和
F/K 都是 finite simple extensions, 利用 Corollary 2.1.4
可得
[L : K]. 例如若
L = K(a1, a2), 我們令 F = K(a1), 則知 L = F(a2). 因此由 L/F 和
F/K 都是 finite simple extensions, 利用 Corollary 2.1.4
可得
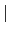
Gal(
L/
F)
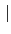
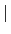
Gal(
F/
K)
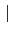
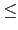
[
L :
F][
F :
K] = [
L :
K].
接著我們只要再探討
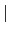 Gal(L/K)
Gal(L/K)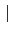 和
和
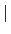 Gal(L/F)
Gal(L/F)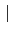
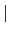 Gal(F/K)
Gal(F/K)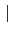 的關係就可得所要的結論. 要得到
的關係就可得所要的結論. 要得到
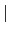 Gal(L/K)
Gal(L/K)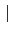 和
和
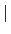 Gal(L/F)
Gal(L/F)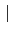
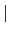 Gal(F/K)
Gal(F/K)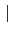 的關係其實並不直接, 不過由於我們想更精準的得到 Galois groups 和
fixed fields 之間的關係, 在此我們就不去探討而選擇另外的方法來處理.
的關係其實並不直接, 不過由於我們想更精準的得到 Galois groups 和
fixed fields 之間的關係, 在此我們就不去探討而選擇另外的方法來處理.
既然 [L : K] 是用 vector space 的 dimension 來定義, 要找到
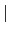 Gal(L/K)
Gal(L/K)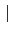 和 [L : K] 的關係, 我們也要想辦法將
Gal(L/K) 和
vector space 扯上關係. 我們考慮的 vector space 是所有從 L 到 L
的函數所成的集合, 即考慮
V = {f : L
和 [L : K] 的關係, 我們也要想辦法將
Gal(L/K) 和
vector space 扯上關係. 我們考慮的 vector space 是所有從 L 到 L
的函數所成的集合, 即考慮
V = {f : L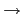 L}. 雖然
Gal(L/K)
中的元素不只是 L 到 L 的函數, 還必須是 ring homomorphism 且是
1-1 and onto, 不過兩個 ring homomorphisms 相加有可能不再是 ring
homomorphism, 而兩個 1-1 and onto 的函數相加也可能不再是 1-1 and
onto. 所以我們不能考慮所有 ring homomorphisms 所成的集合,
也不能考慮所有 1-1 and onto 的函數所成的集合.
它們都無法保持加法封閉, 當然無法形成 vector space.
因此我們必須把條件放寬到考慮所有 L 到 L 的函數. 這時候對於
f, g
L}. 雖然
Gal(L/K)
中的元素不只是 L 到 L 的函數, 還必須是 ring homomorphism 且是
1-1 and onto, 不過兩個 ring homomorphisms 相加有可能不再是 ring
homomorphism, 而兩個 1-1 and onto 的函數相加也可能不再是 1-1 and
onto. 所以我們不能考慮所有 ring homomorphisms 所成的集合,
也不能考慮所有 1-1 and onto 的函數所成的集合.
它們都無法保持加法封閉, 當然無法形成 vector space.
因此我們必須把條件放寬到考慮所有 L 到 L 的函數. 這時候對於
f, g  V 和 c
V 和 c  L, 若我們定義 f + g 和 c . f 這兩個函數為:
對任意
L, 若我們定義 f + g 和 c . f 這兩個函數為:
對任意

 L, f + g 這個函數在
L, f + g 這個函數在  的取值為
f (
的取值為
f ( ) + g(
) + g( ) (即
(f + g)(
) (即
(f + g)( ) = f (
) = f ( ) + g(
) + g( ));
而 c . f 這個函數在
));
而 c . f 這個函數在  的取值為
c . f (
的取值為
c . f ( ) (即
(c . f )(
) (即
(c . f )( ) = c . f (
) = c . f ( )), 則很容易看出 f + g 和
c . f 仍為 L 到 L 的函數 (即
f + g, c . f
)), 則很容易看出 f + g 和
c . f 仍為 L 到 L 的函數 (即
f + g, c . f  V), 且 V
確實為一個 over L 的 vector space.
V), 且 V
確實為一個 over L 的 vector space.
Lemma 2.3.2
假設
L 為一個 field 且

,...,


Aut(
L)
為一組兩兩相異的
L 的 automorphisms. 若考慮

,...,

是
V = {
f :
L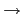 L
L} 這個 vector space over
L 的元素, 則

,...,

是 linearly
independent over
L.
証 明.
考慮
W =
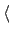

,...,

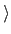
為以

,...,

over
L span 而成的 subspace of
V. 既然

,...,

可展成
W, 要證明

,...,

是 linearly independent over
L, 只要證明
dim
L(
W) =
n 即可.
我們用反證法. 假設
dimL(W) = l < n, 由線性代數的性質知可在
 ,...,
,..., 中找到 l 個元素成為 W over L 的一組
basis. 經過重排, 我們假設
中找到 l 個元素成為 W over L 的一組
basis. 經過重排, 我們假設
 ,...,
,...,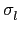 就是 W over
L 的一組 basis. 因為
就是 W over
L 的一組 basis. 因為

 W, 利用 basis 的性質,
我們知道存在唯一的一組
c1,..., cl
W, 利用 basis 的性質,
我們知道存在唯一的一組
c1,..., cl  L 使得
L 使得
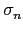 = c1 . = c1 . 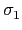 + ... + cl . + ... + cl . 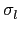 . . |
(2.2) |
因為

不為 0 函數, 一定存在一
ci 
{
c1,...,
cl} 滿足
ci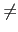
0, 為了方便記, 我們就假設
c1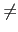
0. 由於

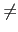

, 必存在

 L
L 使得

(

)
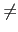

(

). 注意因為

和

是 ring homomorphism, 所以

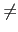
0 (否則會造成

(

) = 0 =

(

)). 現在對任意
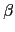
 L
L,
我們將

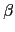
代入

以及
c1 . 
+
... +
cl . 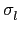
中,
由於它們是相等的函數, 我們得
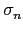 ( (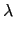 ) )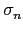 ( (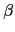 ) ) |
= |
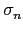 ( (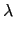 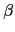 ) ) |
|
| |
= |
c1 . 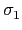 ( (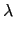 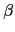 ) + ... + cl . ) + ... + cl . 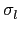 ( (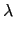 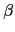 ) ) |
|
| |
= |
c1 . 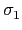 ( (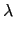 ) )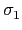 ( (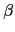 ) + ... + cl . ) + ... + cl . 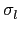 ( (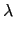 ) )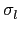 ( (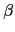 ) ) |
|
因為

是 ring isomorphism 且

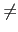
0, 我們知

(

)
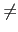
0. 上式兩邊同除

(

), 得
由於這個等式是對所有
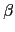
 L 都成立, 所以看成 L 到 L
的函數, 我們有
L 都成立, 所以看成 L 到 L
的函數, 我們有
由於

(

)
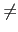

(

) 且
c1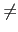
0, 故知
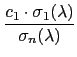
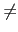 c1
c1.
比較
(
2.2) 和 (
2.3) 兩式, 我們得到

 W
W
有兩種不同用

,...,
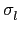
的線性組合的表示法. 這和

,...,
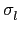
是
W 的一組 basis 相違背, 故知
dim
L(
W) =
l =
n.
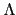
當 L/K 是一個 finite extension, 由 Lemma 2.3.1 我們知
Gal(L/K) 是
Aut(L) 中的一個 finite subgroup, 再利用 Lemma
2.3.2 知
Gal(L/K) 的元素是 linearly independent over L.
由此我們可推得以下重要的性質.
証 明.
假設
Gal(
L/
K) = {

,...,

} 以及
a1,...,
am  L
L 是
L/
K 的一組 basis. 我們利用反證法: 即假設
n >
m 而推得矛盾.
對於任意的
i 
{1,...,
n},
j 
{1,...,
m}, 由於
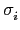

Aut(
L) 且
aj  L
L, 我們有
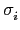
(
aj)
 L
L.
因此可以考慮以下係數在
L 的
n 個變數,
m
個線性方程式的聯立方程式:
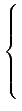 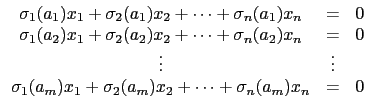 |
(2.4) |
因為變數的個數
n 大於方程式的個數
m,
由線性代數知在
L 中必存在一組不全為 0 的解
c1,...,
cn  L
L
使得
x1 =
c1,...,
xn =
cn 滿足聯立方程式 (
2.4).
也就是說
c1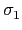 (aj) + c2 (aj) + c2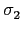 (aj) + ... + cn (aj) + ... + cn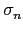 (aj) = 0, (aj) = 0, 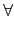 j j 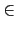 {1,..., m}. {1,..., m}. |
(2.5) |
現因為
a1,..., am 是 L/K 的一組 basis, 對任意

 L
都存在一組
r1,..., rm
L
都存在一組
r1,..., rm  K 使得
K 使得
 = r1a1 + ... + rmam. 若將
= r1a1 + ... + rmam. 若將  代入
c1 .
代入
c1 .  + ... + cn .
+ ... + cn .  這個函數中可得:
這個函數中可得:
(c1 . 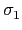 + ... + cn . + ... + cn . 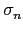 )( )(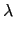 ) ) |
= |
c1 . 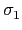 ( (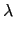 ) + ... + cn . ) + ... + cn . 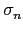 ( (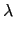 ) ) |
|
| |
= |
c1 . 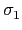 ( (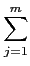 rjaj) + ... + cn . rjaj) + ... + cn . 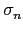 ( (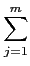 rjaj) rjaj) |
|
| |
= |
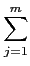 c1 c1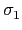 (rjaj) + ... + cn (rjaj) + ... + cn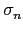 (rjaj). (rjaj). |
|
由於
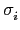

Gal(
L/
K) 將
K 中的元素都固定以及式子
(
2.5), 我們得
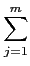 c1 c1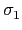 (rjaj) + ... + cn (rjaj) + ... + cn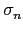 (rjaj) (rjaj) |
= |
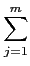 c1rj c1rj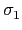 (aj) + ... + cnrj (aj) + ... + cnrj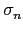 (aj) (aj) |
|
| |
= |
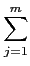 rj(c1 rj(c1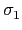 (aj) + ... + cn (aj) + ... + cn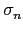 (aj)) (aj)) |
|
| |
= |
0. |
|
也就是說對任意

 L
L 代入
c1 . 
+
... +
cn . 
這個函數後都得到 0,
故得
c1 . 
+
... +
cn . 
是一個零函數 (即
c1 . 
+
... +
cn . 
= 0). 由於
c1,...,
cn  L
L 是
L 中一組不全為 0 的數,
c1 . 
+
... +
cn . 
= 0 和 Lemma
2.3.2
所知

,...,

是 linearly independent over
L
相矛盾, 故得證
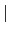
Gal(
L/
K)
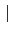
=
n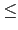 m
m = [
L :
K].
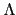
利用類似的方法, 我們可以得到以下更好的結果, 讓我們更清楚 Galois
group 和 fixed field 之間的關係.
Theorem 2.3.4
假設
L/
K 是一個 finite extension 且
H 是
Gal(
L/
K) 的
subgroup. 則
証 明.
回顧一下

(
H) =
LH 是
H 的 fixed field 而且是
L/
K 的
intermediate field. 若考慮
L/

(
H) 這一個 extension, 當然也是
finite extension, 故套用 Proposition
2.3.3, 得
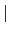
Gal(
L/

(
H))
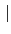
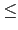
[
L :

(
H)]. 依定義
Gal(
L/

(
H)) =
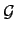
(

(
H)), 故由 Proposition
2.2.3 知
H 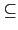
Gal(
L/

(
H)), 而得
假設
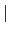 H
H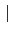
=
n, 若我們能證明任取
L 中
n + 1 個元素必定 linearly
dependent over

(
H), 則知
[
L :

(
H)]
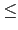 n
n =
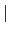 H
H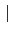
. 故得證
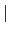 H
H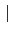
= [
L :

(
H)].
假設
H = {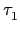 ,...,
,...,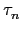 }, 其中
}, 其中 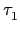 = I 是 identity. 任取
a1,..., an + 1
= I 是 identity. 任取
a1,..., an + 1  L, 我們欲證明
a1,..., an + 1 是 linearly
dependent over
L, 我們欲證明
a1,..., an + 1 是 linearly
dependent over
 (H). 首先我們考慮以下係數在 L 的 n + 1 個變數,
n 個線性方程式的聯立方程式:
(H). 首先我們考慮以下係數在 L 的 n + 1 個變數,
n 個線性方程式的聯立方程式:
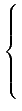 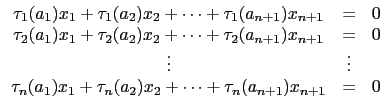 |
(2.6) |
注意因
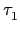
=
I 所以聯立方程式 (
2.6)
中的第一個式子其實是
a1x1 + a2x2 + ... + an + 1xn + 1 = 0.
若我們能證明聯立方程式 (
2.6) 在

(
H)
中存在一組不全為 0 的解
c1,...,
cn + 1 

(
H), 則得
c1a1 + c2a2 + ... + cn + 1an + 1 = 0,
故知
a1,...,
an + 1
是 linearly dependent over

(
H).
現由於聯立方程式 (2.6) 變數的個數 n + 1 大於方程式的個數
n, 由線性代數知在 L 中必存在一組不全為 0 的解.
我們考慮所有聯立方程式 (2.6) 的解中不等於 0
的項數最少的一組解. 經過重排我們假設
x1 = b1,..., xn + 1 = bn + 1
是聯立方程式 (2.6) 的一組解, 其中這些 bi  L 且
b1,..., bm
L 且
b1,..., bm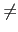 0 以及
bm + 1,..., bn + 1 = 0.
依我們的找法知若在 L 中找到一組解且其不等於 0 的項數少於 m,
則這一組解必全等於 0. 又因為 b1
0 以及
bm + 1,..., bn + 1 = 0.
依我們的找法知若在 L 中找到一組解且其不等於 0 的項數少於 m,
則這一組解必全等於 0. 又因為 b1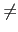 0, 且聯立方程式
(2.6) 是線性的, 同除以 b1 我們知
0, 且聯立方程式
(2.6) 是線性的, 同除以 b1 我們知
x1 = 1, x2 = b2/b1,..., xm = bm/b1, xm + 1 = 0,..., xn + 1 = 0
仍然是聯立方程式 (
2.6) 的一組不全為 0 的解. 為了方便我們將
bi/
b1 記為
ci, 也就是說我們有以下的等式:
 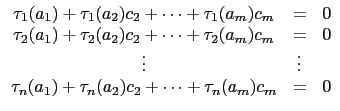 |
(2.7) |
這些
c2,...,
cm 是在
L 中皆不為 0 的數, 我們要證明這些
c2,...,
cm 事實上是在

(
H)
中. 依定義

(
H) 是被所有
H 的元素固定的
L
中的元素所成的集合, 因此要證明
ci 

(
H), 我們只要證明對任意
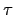
 H
H 皆有
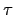
(
ci) =
ci. 所以對任意
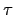
 H
H
我們將之作用於式子 (
2.7) 中的每一個式子得到對任意
j 
{1,...,
n}, 皆有
| 0 |
= |
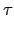 ( (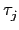 (a1) + (a1) + 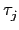 (a2)c2 + ... + (a2)c2 + ... + 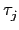 (am)cm) (am)cm) |
|
| |
= |
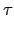 ( (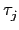 (a1)) + (a1)) + 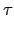 ( (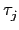 (a2)) (a2))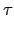 (c2) + ... + (c2) + ... + 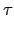 ( (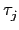 (am)) (am))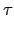 (cm) (cm) |
|
| |
= |
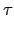 o o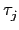 (a1) + (a1) + 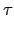 o o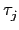 (a2) (a2)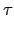 (c2) + ... + (c2) + ... + 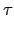 o o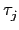 (am) (am)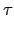 (cm) (cm) |
|
由於
H 是一個 group 且
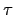
 H
H, 故對任意
j = {1,...,
n}
皆存在唯一的
j' 
{1,...,
n} 滿足
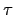 o
o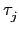
=
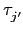
.
因此我們可以將上式改寫成
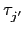
(
a1) +
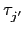
(
a2)
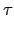
(
c2) +
... +
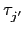
(
am)
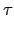
(
cm) = 0.
再加上若
j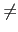 k
k, 則
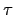 o
o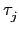
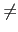
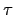 o
o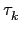
, 因此當
j 跑遍所有的 1,...,
n 時, 所對應的
j' 也跑遍所有的
1,...,
n. 因此上式的是對任意的
j' 
{1,...,
n} 都成立的,
也就是說我們有以下的等式:
換言之對任意
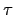
 H
H,
x1 = 1,
x2 =
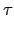
(
c2),...,
xm =
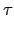
(
cm),
xm + 1 = 0,...,
xn + 1 = 0
是聯立方程式 (
2.6) 的一組解. 由於
x1 = 1, x2 = c2,..., xm = cm, xm + 1 = 0,..., xn + 1 = 0
已是聯立方程式 (
2.6) 的一組解且聯立方程式 (
2.6)
是線性的, 所以知
x1 = 1 - 1 = 0,
x2 =
c2 -
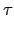
(
c2),...,
xm =
cm -
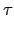
(
cm),
xm + 1 = 0,...,
xn + 1 = 0
也是聯立方程式 (
2.6)
的一組解. 很顯然的這一組解不等於 0 的項數少於
m, 但當初我們假設
m 是所有不全為 0 的解中不為 0 的項數最少的. 因此知這組解應全為
0, 也就是說
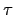
(
c2) =
c2,...,
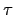
(
cm) =
cm. 又這是對任意
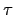
 H
H 都成立的, 故得
c2,...,
cm 

(
H). 故再由
c2,...,
cm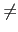
0 以及
a1 +
c2a2 +
... +
cmam = 0, 知
a1,...,
am 是 linearly dependent over

(
H). 所以當然
a1,...,
am,...,
an + 1 是 linearly dependent over

(
H),
得證本定理.
利用 Theorem 2.3.4 我們馬上可推導出一些有用的性質.
証 明.
由於
K 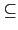

(
H)
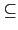 L
L, 利用 Lemma
1.2.3 我們知
[
L :
K] = [
L :

(
H)][

(
H) :
K]. 再利用 Theorem
2.3.4 我們知
[
L :

(
H)] =
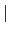 H
H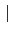
, 故得證.
Corollary 2.3.6
假設
L/
K 是一個 finite extension 且
H 是
Gal(
L/
K) 的
subgroup, 則
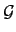
(
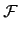
(
H)) =
H.
証 明.
由 Proposition
2.2.3 我們知
H 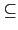
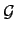
(

(
H)),
因此若要證得
H =
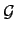
(

(
H)) 只要檢查是否
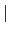 H
H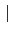
=
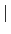
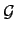
(

(
H))
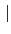
. 由於
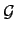
(

(
H)) 仍為
Gal(
L/
K) 的
subgroup, 故由 Theorem
2.3.4 知
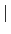
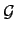
(

(
H))
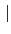
= [
L :

(
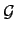
(

(
H)))]. 又由於

(
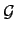
(

(
H))) =

(
H) (Proposition
2.2.3) 故知
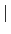
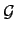
(

(
H))
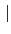
= [
L :

(
H)] =
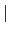 H
H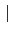
. 得證
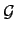
(

(
H)) =
H.
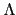
回顧一下, 當 L/K 是一個 finite extension, 我們令
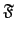 是
L/K 的 intermediate fields 所成的集合且令
是
L/K 的 intermediate fields 所成的集合且令
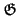 是
Gal(L/K) 的 subgroups 所成的集合, 而
是
Gal(L/K) 的 subgroups 所成的集合, 而
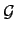 :
: 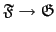 是一個從
是一個從
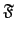 到
到
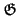 的函數, 且
的函數, 且
 :
: 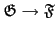 是一個從
是一個從
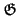 到
到
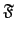 的函數. Corollary 2.3.6 告訴我們當
H
的函數. Corollary 2.3.6 告訴我們當
H 
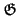 時
時
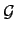 (
( (H)) = H,
也就是說
(H)) = H,
也就是說
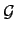 o
o :
: 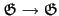 是一個從
是一個從
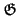 送到
送到
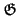 的
identity map. 因此我們知
的
identity map. 因此我們知
 這個函數是 1-1 (因為若
這個函數是 1-1 (因為若
 (H1) =
(H1) =  (H2), 將之代入
(H2), 將之代入
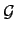 得 H1 = H2) 而
得 H1 = H2) 而
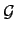 是 onto
(對任意
H
是 onto
(對任意
H 
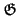 , 取
F =
, 取
F =  (H)
(H) 
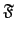 , 可得
, 可得
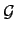 (F) = H). 在 Example
2.1.5 中我們知一般來說
(F) = H). 在 Example
2.1.5 中我們知一般來說
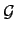 不一定是 1-1, 以後我們將探討何時
不一定是 1-1, 以後我們將探討何時
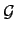 會是 1-1.
會是 1-1.



下一頁: Normal Extension 和 Separable
上一頁: Galois Group 和 Fixed
前一頁: Fixed Field
目 錄
Li
2006-05-18
![]() Gal(L/K)
Gal(L/K)![]()
![]() [L : K]. 所以知道在這情形時
Gal(L/K) 是一個 finite group. 事實上不需 simple 的假設, 當 L/K
是 finite extension 時
Gal(L/K) 必是一個 finite group.
[L : K]. 所以知道在這情形時
Gal(L/K) 是一個 finite group. 事實上不需 simple 的假設, 當 L/K
是 finite extension 時
Gal(L/K) 必是一個 finite group.
![]()
![]() Gal(L/K) 時,
Gal(L/K) 時,
![]() (ai) 有哪些可能的取值呢? 若
fi(x)
(ai) 有哪些可能的取值呢? 若
fi(x) ![]() K[x] 是 ai over K 的 minimal polynomial, 且
deg(fi(x)) = mi, 則由於
K[x] 是 ai over K 的 minimal polynomial, 且
deg(fi(x)) = mi, 則由於
![]() Gal(L/K)
Gal(L/K)![]() = s1 ... sn.
這是因為任意給定
= s1 ... sn.
這是因為任意給定
![]() ,...,
,...,![]()
![]() L 分別為
f1(x) = 0,..., fn(x) 在 L 的根, 並不能保證存在
L 分別為
f1(x) = 0,..., fn(x) 在 L 的根, 並不能保證存在
![]()
![]() Gal(L/K) 會同時滿足
Gal(L/K) 會同時滿足
![]() (a1) =
(a1) = ![]() ,...,
,...,![]() (an) =
(an) = ![]() .
.
![]() Gal(L/K)
Gal(L/K)![]()
![]() [L : K]. 例如若
L = K(a1, a2), 我們令 F = K(a1), 則知 L = F(a2). 因此由 L/F 和
F/K 都是 finite simple extensions, 利用 Corollary 2.1.4
可得
[L : K]. 例如若
L = K(a1, a2), 我們令 F = K(a1), 則知 L = F(a2). 因此由 L/F 和
F/K 都是 finite simple extensions, 利用 Corollary 2.1.4
可得
![]() Gal(L/K)
Gal(L/K)![]() 和 [L : K] 的關係, 我們也要想辦法將
Gal(L/K) 和
vector space 扯上關係. 我們考慮的 vector space 是所有從 L 到 L
的函數所成的集合, 即考慮
V = {f : L
和 [L : K] 的關係, 我們也要想辦法將
Gal(L/K) 和
vector space 扯上關係. 我們考慮的 vector space 是所有從 L 到 L
的函數所成的集合, 即考慮
V = {f : L![]() L}. 雖然
Gal(L/K)
中的元素不只是 L 到 L 的函數, 還必須是 ring homomorphism 且是
1-1 and onto, 不過兩個 ring homomorphisms 相加有可能不再是 ring
homomorphism, 而兩個 1-1 and onto 的函數相加也可能不再是 1-1 and
onto. 所以我們不能考慮所有 ring homomorphisms 所成的集合,
也不能考慮所有 1-1 and onto 的函數所成的集合.
它們都無法保持加法封閉, 當然無法形成 vector space.
因此我們必須把條件放寬到考慮所有 L 到 L 的函數. 這時候對於
f, g
L}. 雖然
Gal(L/K)
中的元素不只是 L 到 L 的函數, 還必須是 ring homomorphism 且是
1-1 and onto, 不過兩個 ring homomorphisms 相加有可能不再是 ring
homomorphism, 而兩個 1-1 and onto 的函數相加也可能不再是 1-1 and
onto. 所以我們不能考慮所有 ring homomorphisms 所成的集合,
也不能考慮所有 1-1 and onto 的函數所成的集合.
它們都無法保持加法封閉, 當然無法形成 vector space.
因此我們必須把條件放寬到考慮所有 L 到 L 的函數. 這時候對於
f, g ![]() V 和 c
V 和 c ![]() L, 若我們定義 f + g 和 c . f 這兩個函數為:
對任意
L, 若我們定義 f + g 和 c . f 這兩個函數為:
對任意
![]()
![]() L, f + g 這個函數在
L, f + g 這個函數在 ![]() 的取值為
f (
的取值為
f (![]() ) + g(
) + g(![]() ) (即
(f + g)(
) (即
(f + g)(![]() ) = f (
) = f (![]() ) + g(
) + g(![]() ));
而 c . f 這個函數在
));
而 c . f 這個函數在 ![]() 的取值為
c . f (
的取值為
c . f (![]() ) (即
(c . f )(
) (即
(c . f )(![]() ) = c . f (
) = c . f (![]() )), 則很容易看出 f + g 和
c . f 仍為 L 到 L 的函數 (即
f + g, c . f
)), 則很容易看出 f + g 和
c . f 仍為 L 到 L 的函數 (即
f + g, c . f ![]() V), 且 V
確實為一個 over L 的 vector space.
V), 且 V
確實為一個 over L 的 vector space.
![]() ,...,
,...,![]() 中找到 l 個元素成為 W over L 的一組
basis. 經過重排, 我們假設
中找到 l 個元素成為 W over L 的一組
basis. 經過重排, 我們假設
![]() ,...,
,...,![]() 就是 W over
L 的一組 basis. 因為
就是 W over
L 的一組 basis. 因為
![]()
![]() W, 利用 basis 的性質,
我們知道存在唯一的一組
c1,..., cl
W, 利用 basis 的性質,
我們知道存在唯一的一組
c1,..., cl ![]() L 使得
L 使得
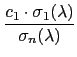
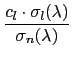
![]()
![]() L 都成立, 所以看成 L 到 L
的函數, 我們有
L 都成立, 所以看成 L 到 L
的函數, 我們有 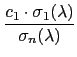
![]()
![]() L
都存在一組
r1,..., rm
L
都存在一組
r1,..., rm ![]() K 使得
K 使得
![]() = r1a1 + ... + rmam. 若將
= r1a1 + ... + rmam. 若將 ![]() 代入
c1 .
代入
c1 . ![]() + ... + cn .
+ ... + cn . ![]() 這個函數中可得:
這個函數中可得:
![]() ,...,
,...,![]() }, 其中
}, 其中 ![]() = I 是 identity. 任取
a1,..., an + 1
= I 是 identity. 任取
a1,..., an + 1 ![]() L, 我們欲證明
a1,..., an + 1 是 linearly
dependent over
L, 我們欲證明
a1,..., an + 1 是 linearly
dependent over
![]() (H). 首先我們考慮以下係數在 L 的 n + 1 個變數,
n 個線性方程式的聯立方程式:
(H). 首先我們考慮以下係數在 L 的 n + 1 個變數,
n 個線性方程式的聯立方程式:
![]() L 且
b1,..., bm
L 且
b1,..., bm![]() 0 以及
bm + 1,..., bn + 1 = 0.
依我們的找法知若在 L 中找到一組解且其不等於 0 的項數少於 m,
則這一組解必全等於 0. 又因為 b1
0 以及
bm + 1,..., bn + 1 = 0.
依我們的找法知若在 L 中找到一組解且其不等於 0 的項數少於 m,
則這一組解必全等於 0. 又因為 b1![]() 0, 且聯立方程式
(2.6) 是線性的, 同除以 b1 我們知
0, 且聯立方程式
(2.6) 是線性的, 同除以 b1 我們知