


下一頁: Extension Degree 和 Galois
上一頁: Galois Group 和 Fixed
前一頁: Galois Group
目 錄
當 L 是一個 field,

 Aut(L) 若
Aut(L) 若

 L 滿足
L 滿足
 (
( ) =
) =  , 我們就稱
, 我們就稱  被
被  固定
(fixed). 我們用 L
固定
(fixed). 我們用 L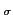 表示在 L 中所有被
表示在 L 中所有被  固定的元素所成的集合. L
固定的元素所成的集合. L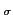 事實上是一個 field, 我們稱之為
事實上是一個 field, 我們稱之為
 的 fixed field. 這一節中我們主要是介紹 fixed field 以及其和
Galois group 的關係.
的 fixed field. 這一節中我們主要是介紹 fixed field 以及其和
Galois group 的關係.
首先我們來看 L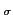 為何是一個 field. 若
為何是一個 field. 若
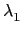 ,
,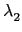
 L
L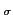 , 且
, 且
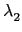
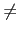 0 則由於
0 則由於
 (
(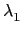 ) =
) = 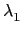 ,
,
 (
(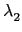 ) =
) = 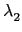 以及
以及

 Aut(L), 可得
Aut(L), 可得
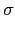
(
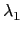
-
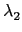
) =
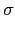
(
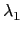
) -
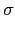
(
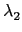
) =
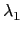
-
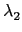
and
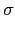
(
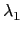
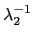
) =
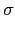
(
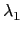
)
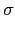
(
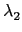
)
-1 =
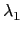
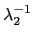
.
因此
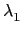 -
- 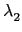
 L
L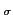 以及
以及
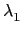
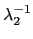
 L
L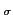 , 故知 L
, 故知 L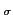 是一個 field.
特別當 L/K 是一個 field extension 且
是一個 field.
特別當 L/K 是一個 field extension 且

 Gal(L/K), 則由於
K 中的元素皆被
Gal(L/K), 則由於
K 中的元素皆被  , 固定我們有
K
, 固定我們有
K  L
L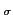
 L, 換言之 L
L, 換言之 L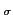 是 L/K 的 intermediate field.
是 L/K 的 intermediate field.
在前一節中我們定義了一個函數
 將 L/K 的 intermediate fields
送到
Gal(L/K) 的 subgroups. 一般來說
將 L/K 的 intermediate fields
送到
Gal(L/K) 的 subgroups. 一般來說
 不一定是 1-1 (參見
Example 2.1.5), 為了探討何時
不一定是 1-1 (參見
Example 2.1.5), 為了探討何時
 會 1-1,
以下我們引進了一個反向的函數將
Gal(L/K) 的 subgroups 送到 L/K
的 intermediate fields.
會 1-1,
以下我們引進了一個反向的函數將
Gal(L/K) 的 subgroups 送到 L/K
的 intermediate fields.
首先若 H 是
Gal(L/K) 的一個 subgroup 我們定義
LH = {
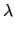
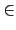 L
L |
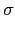
(
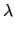
) =
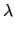
,
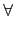
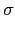
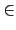 H
H} =
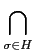 L
L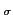
.
利用 fields 的交集仍是 field
以及對任意

 H
H  Gal(L/K) 皆有
K
Gal(L/K) 皆有
K  L
L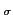 , 我們知 LH 仍為一個 field 且
K
, 我們知 LH 仍為一個 field 且
K  LH
LH  L. 故得 LH 仍為 L/K 的 intermediate field.
L. 故得 LH 仍為 L/K 的 intermediate field.
Definition 2.2.1
當
L/
K 是一個 field extension 且
H 是
Gal(
L/
K) 的一個
subgroup, 我們稱
LH = {

 L
L |

(

) =

,
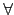

 H
H} 為
H 的
fixed field.
回顧上一節中當 L/K 是一個 field extension, 我們令
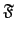 是 L/K 的 intermediate fields 所成的集合且令
是 L/K 的 intermediate fields 所成的集合且令
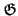 是
Gal(L/K) 的 subgroups 所成的集合. 現在我們可以定義一個函數
是
Gal(L/K) 的 subgroups 所成的集合. 現在我們可以定義一個函數
 :
: 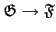 使得對任意
Gal(L/K) 的 subgroup H (即
H
使得對任意
Gal(L/K) 的 subgroup H (即
H 
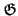 ), 我們定義
), 我們定義
 (H) = LH. 從前面的討論我們知 LH 是 L/K
的一個 intermediate field, 也就是說
(H) = LH. 從前面的討論我們知 LH 是 L/K
的一個 intermediate field, 也就是說
 (H)
(H) 
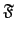 , 因此
, 因此
 確實是一個 well-defined 函數.
確實是一個 well-defined 函數.
當 I 是
Gal(L/K) 的 identity 時, 當然有 LI = L, 因此由定義知
 ({I}) = L. 要注意的是雖然
Gal(L/K) 將 K 的元素都固定, 但是
Gal(L/K) 的 fixed field 可能比 K 還大, 所以一般的情形不見得有
({I}) = L. 要注意的是雖然
Gal(L/K) 將 K 的元素都固定, 但是
Gal(L/K) 的 fixed field 可能比 K 還大, 所以一般的情形不見得有
 (Gal(L/K)) = K (後面我們會舉一個例子). 對於函數
(Gal(L/K)) = K (後面我們會舉一個例子). 對於函數
 我們有和
我們有和
 相對應的性質 (Lemma 2.1.2).
相對應的性質 (Lemma 2.1.2).
Lemma 2.2.2
給定一 extension
L/
K, 若
H1,
H2 
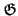
是
Gal(
L/
K) 之兩個
subgroups 且滿足
H1  H2
H2, 則

(
H2)


(
H1).
証 明.
若



(
H2) =
LH2, 表示對任意

 H2
H2 皆滿足

(

) =

. 現任取
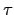
 H1
H1, 由於
H1  H2
H2, 我們有
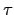
 H2
H2, 故由



(
H2) 的假設知
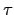
(

) =

, 因此

 LH1
LH1 =

(
H1). 得證

(
H2)


(
H1).
再次強調:
 是將 L/K 的 intermediate fields 送到
Gal(L/K)
的 subgroups, 而
是將 L/K 的 intermediate fields 送到
Gal(L/K)
的 subgroups, 而
 是將
Gal(L/K) 的 subgroups 送到 L/K 的
intermediate fields. 以下是這兩個函數相互的關係.
是將
Gal(L/K) 的 subgroups 送到 L/K 的
intermediate fields. 以下是這兩個函數相互的關係.
証 明.
(1) 首先觀察若
F 是
L/
K 的 intermediate field, 則

(
F) = Gal(
L/
F), 換言之對任意的



(
F) 都會將
F
中的元素固定. 因此若

 F
F, 則對任意



(
F)
皆滿足

(

) =

, 也就是說

 L
L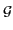 (F)
(F) =

(

(
F)). 故得證
F 

(

(
F)). 另一方面,
若
H 是
Gal(
L/
K) 的 subgroup, 則

(
H) 中的元素都會被
H
固定住. 因此若

 H
H, 則


Aut
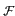 (H)
(H)(
L) = Gal(
L/

(
H)) =

(

(
H)). 故得證
H 

(

(
H)).
(2) 由於 F 和
 (
( (F)) 皆為 L/K 的 intermediate fields,
利用 (1)
F
(F)) 皆為 L/K 的 intermediate fields,
利用 (1)
F 
 (
( (F)) 以及 Lemma 2.1.2 我們得到
(F)) 以及 Lemma 2.1.2 我們得到
 (
( (
( (F)))
(F))) 
 (F). 然而
(F). 然而
 (F) 是
Gal(L/K) 的
subgroup, 故將 (1) 的 H 用
(F) 是
Gal(L/K) 的
subgroup, 故將 (1) 的 H 用
 (F) 取代, 可得
(F) 取代, 可得
 (F)
(F) 
 (
( (
( (F))). 因此得證
(F))). 因此得證
 (F) =
(F) =  (
( (
( (F))). 另一方面因為
H 和
(F))). 另一方面因為
H 和
 (
( (H)) 皆為
Gal(L/K) 的 subgroups, 利用 (1)
H
(H)) 皆為
Gal(L/K) 的 subgroups, 利用 (1)
H 
 (
( (H)) 以及 Lemma 2.2.2 我們得到
(H)) 以及 Lemma 2.2.2 我們得到
 (
( (
( (H)))
(H))) 
 (H). 然而
(H). 然而
 (H) 是 L/K 的
intermediate field, 故將 (1) 的 F 用
(H) 是 L/K 的
intermediate field, 故將 (1) 的 F 用
 (H) 取代, 可得
(H) 取代, 可得
 (H)
(H) 
 (
( (
( (H))). 因此得證
(H))). 因此得證
 (H) =
(H) =  (
( (
( (H))).
(H))). 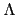
在一般的情形 Proposition 2.2.3 (1) 的等式有可能不成立 (即
F 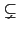
 (
( (F)) 和
H
(F)) 和
H 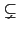
 (
( (H))
的情形有可能發生). 以後我們會知道當 L/K 是 finite extension 時,
對任意
Gal(L/K) 的 subgroup H 皆有
H =
(H))
的情形有可能發生). 以後我們會知道當 L/K 是 finite extension 時,
對任意
Gal(L/K) 的 subgroup H 皆有
H =  (
( (H)) 的性質.
不過對於 L/K 的 intermediate field F, 仍可能有
F
(H)) 的性質.
不過對於 L/K 的 intermediate field F, 仍可能有
F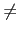
 (
( (F))
的情形發生 (下面我們會給一個例子). Galois 的理論就是要探討在哪些
extension L/K, 對任意的 L/K 的 intermediate field F 皆有
F =
(F))
的情形發生 (下面我們會給一個例子). Galois 的理論就是要探討在哪些
extension L/K, 對任意的 L/K 的 intermediate field F 皆有
F =  (
( (F)) 的性質.
(F)) 的性質.
以下我們利用前一節的例子, 來探討 Galois groups 和 fixed fields
之間的關係.
Example 2.2.4
我們沿用 Example
2.1.5 的 extension, 即
L =

(

) 其中

是
x4 - 2 唯一的正實根. 此時我們知
Gal(
L/

) = {
I,

}, 其中

(

) = -

. 又
F =

(
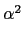
) 為
L/

的 intermediate field 且

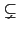 F
F 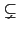 L
L.
Gal(L/ ) 只有兩個 subgroups: 即 {I} 和
Gal(L/
) 只有兩個 subgroups: 即 {I} 和
Gal(L/ ). 已知
). 已知
 ({I}) = L, 我們來探討
({I}) = L, 我們來探討
 (Gal(L/
(Gal(L/ )) 應該是哪一個 field.
由於
)) 應該是哪一個 field.
由於

(Gal(
L/

)) =
LI 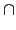 L
L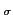
=
L 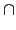 L
L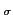
=
L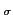
,
我們只要探討

的 fixed field 即可.
由於對任意 L 中的元素  都可唯一表示成
都可唯一表示成
 = r0 + r1
= r0 + r1 + r2
+ r2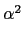 + r3
+ r3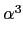 , 其中
r1, r2, r3, r4
, 其中
r1, r2, r3, r4 
 . 若
. 若

 L
L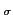 , 我們有
, 我們有
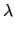
=
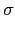
(
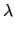
) =
r0 +
r1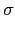
(
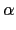
) +
r2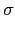
(
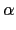
)
2 +
r3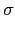
(
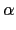
)
3 =
r0 -
r1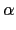
+
r2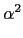
-
r3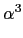
.
因此得知
r1 =
r3 = 0, 也就是說
L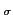
中的元素必可寫成
r0 +
r2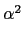
, 其中
r0,
r2 

這種形式. 故得
L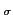


(
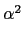
) =
F. 另一方面在 Example
2.1.5
中我們知
F 中的元素都被

固定, 故得
F  L
L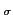
.
因此得證
L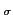
=
F, 也就是說

(Gal(
L/

)) =
F. 要注意,
我們曾經提過在一般的情形
Gal(
L/
K) 的 fixed field 不一定是
K,
在我們這個例子

(Gal(
L/

)) =
F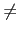

, 就是這種情形.
在 Example 2.1.5 我們已知
 (
( ) =
) =  (F) = Gal(L/
(F) = Gal(L/ ) 以及
) 以及
 (L) = {I}. 因此我們有
(L) = {I}. 因此我們有

(

(

)) =

(

(
F)) =

(Gal(
L/

)) =
F and

(

(
L)) =

({
I}) =
L.
因此知

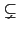

(

(

)),
F =

(

(
F)) and
L =

(

(
L)).
要注意

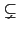

(

(

)) 就是
Proposition
2.2.3 (1) 等式不成立的一個例子.
另一方面我們有
 (
( ({I})) =
({I})) =  (L) 且
(L) 且
 (
( (Gal(L/
(Gal(L/ ))) =
))) =  (F) 因此知
(F) 因此知
{
I} =

(

({
I})) and Gal(
L/

) =

(

(Gal(
L/

))).
Example 2.2.5
在這個例子我們沿用 Example
2.1.6 的 extension, 即
L =

(

) 其中

=
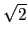
+
i. 此時我們知
Gal(
L/

) = {
I,
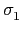
,
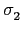
,
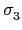
}, 其中
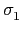
(

) = -

,
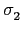
(

) = 3
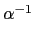
以及
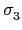
(

) = - 3
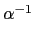
. 另外
L/

有三個相異的
nontrivial intermediate fields, 分別為
F1 =

(
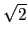 i
i),
F2 =

(
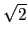
) 以及
F3 =

(
i).
在 Example 2.1.6 我們已知
Gal(L/ )
) 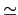
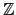 /2
/2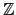 ×
×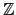 /2
/2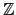 所以
Gal(L/
所以
Gal(L/ ) 共有 5
個 subgroups: {I},
Gal(L/
) 共有 5
個 subgroups: {I},
Gal(L/ ),
H1 = {I,
),
H1 = {I,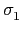 },
H2 = {I,
},
H2 = {I,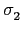 } 以及
H3 = {I,
} 以及
H3 = {I,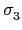 }. 我們先探討
}. 我們先探討
 在這 5 個 subgroups 的取值. 首先我們已知
在這 5 個 subgroups 的取值. 首先我們已知
 ({I}) = L. 對於
({I}) = L. 對於
 (H1), 由於
(H1), 由於
我們只要探討
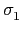
的 fixed field
即可. 不過在 Exampel
2.1.6, 我們知道
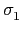
會固定
F1
的所有元素, 因此知
F1  L
L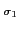
. 如果
F1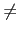 L
L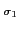
, 即
[
L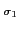
:
F1] > 1, 由 Lemma
1.2.3 知
2 = [
L :
F1] = [
L :
L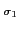
][
L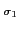
:
F1] > [
L :
L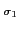
],
這迫使
[
L :
L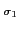
] = 1, 也就是說
L =
L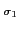
.
不過這是不可能的因為

 L
L 但
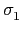
(

) = -

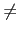

, 也就是說

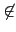 L
L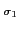
. 由此矛盾知
F1 =
L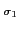
=
LH1 =

(
H1).
同理可得
F2 =

(
H2) 以及
F3 =

(
H3). 至於

(Gal(
L/

)), 由定義以及前面結果知
如果
F2 =
F1 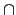 F2
F2 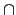 F3
F3,
表示
F2  F1
F1 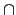 F3
F3  F3
F3, 這是不可能的 (因為
[
F2 :

] = [
F3 :

] = 2, 因此
F2  F3
F3 會導致
F2 =
F3).
故知
F2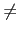 F1
F1 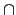 F2
F2  F3
F3, 也就是說
[
F2 :

(Gal(
L/

))] > 1. 再次利用 Lemma
1.2.3 知
2 = [
F2 :

] = [
F2 :

(Gal(
L/

))][

(Gal(
L/

)) :

] > [

(Gal(
L/

)) :

],
故得
[

(Gal(
L/

)) :

] = 1, 也就是說

(Gal(
L/

)) =

.
因此我們知

這個函數對
Gal(
L/

) 的 subgroups 取值分別為:

({
I}) =
L,

(
H1) =
F1,

(
H2) =
F2,

(
H3) =
F3 and

(Gal(
L/

)) =

.
由 Example
2.1.6 我們知

(
L) = {
I},

(
F1) =
H2,

(
F2) =
H2,

(
F3) =
H3 and

(

) = Gal(
L/

),
因此我們有
L =

(

(
L)),
F1 =

(

(
F1)),
F2 =

(

(
F2)),
F3 =

(

(
F3)) and

=

(

(

)),
以及
{
I} =

(

({
I})),
H1 =

(

(
H2)),
H2 =

(

(
H2)),
H3 =

(

(
H3)) and Gal(
L/

) =

(

(Gal(
L/

))).
以後我們會知道
L/ 的 intermediate fields 只有
的 intermediate fields 只有
 , F1,
F2, F3 以及 L, 因此知
, F1,
F2, F3 以及 L, 因此知
 :
: 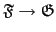 和
和
 :
: 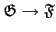 互為反函數, 也就是說
互為反函數, 也就是說
 和
和
 都是 1-1 且 onto. 這種 extension
就是所謂的 Galois Extension.
都是 1-1 且 onto. 這種 extension
就是所謂的 Galois Extension.



下一頁: Extension Degree 和 Galois
上一頁: Galois Group 和 Fixed
前一頁: Galois Group
目 錄
Li
2006-05-18
![]() 為何是一個 field. 若
為何是一個 field. 若
![]() ,
,![]()
![]() L
L![]() , 且
, 且
![]()
![]() 0 則由於
0 則由於
![]() (
(![]() ) =
) = ![]() ,
,
![]() (
(![]() ) =
) = ![]() 以及
以及
![]()
![]() Aut(L), 可得
Aut(L), 可得
![]() 將 L/K 的 intermediate fields
送到
Gal(L/K) 的 subgroups. 一般來說
將 L/K 的 intermediate fields
送到
Gal(L/K) 的 subgroups. 一般來說
![]() 不一定是 1-1 (參見
Example 2.1.5), 為了探討何時
不一定是 1-1 (參見
Example 2.1.5), 為了探討何時
![]() 會 1-1,
以下我們引進了一個反向的函數將
Gal(L/K) 的 subgroups 送到 L/K
的 intermediate fields.
會 1-1,
以下我們引進了一個反向的函數將
Gal(L/K) 的 subgroups 送到 L/K
的 intermediate fields.
![]() 是 L/K 的 intermediate fields 所成的集合且令
是 L/K 的 intermediate fields 所成的集合且令
![]() 是
Gal(L/K) 的 subgroups 所成的集合. 現在我們可以定義一個函數
是
Gal(L/K) 的 subgroups 所成的集合. 現在我們可以定義一個函數
![]() :
: ![]() 使得對任意
Gal(L/K) 的 subgroup H (即
H
使得對任意
Gal(L/K) 的 subgroup H (即
H ![]()
![]() ), 我們定義
), 我們定義
![]() (H) = LH. 從前面的討論我們知 LH 是 L/K
的一個 intermediate field, 也就是說
(H) = LH. 從前面的討論我們知 LH 是 L/K
的一個 intermediate field, 也就是說
![]() (H)
(H) ![]()
![]() , 因此
, 因此
![]() 確實是一個 well-defined 函數.
確實是一個 well-defined 函數.
![]() ({I}) = L. 要注意的是雖然
Gal(L/K) 將 K 的元素都固定, 但是
Gal(L/K) 的 fixed field 可能比 K 還大, 所以一般的情形不見得有
({I}) = L. 要注意的是雖然
Gal(L/K) 將 K 的元素都固定, 但是
Gal(L/K) 的 fixed field 可能比 K 還大, 所以一般的情形不見得有
![]() (Gal(L/K)) = K (後面我們會舉一個例子). 對於函數
(Gal(L/K)) = K (後面我們會舉一個例子). 對於函數
![]() 我們有和
我們有和
![]() 相對應的性質 (Lemma 2.1.2).
相對應的性質 (Lemma 2.1.2).
![]() 是將 L/K 的 intermediate fields 送到
Gal(L/K)
的 subgroups, 而
是將 L/K 的 intermediate fields 送到
Gal(L/K)
的 subgroups, 而
![]() 是將
Gal(L/K) 的 subgroups 送到 L/K 的
intermediate fields. 以下是這兩個函數相互的關係.
是將
Gal(L/K) 的 subgroups 送到 L/K 的
intermediate fields. 以下是這兩個函數相互的關係.
![]() (
(![]() (F)) 皆為 L/K 的 intermediate fields,
利用 (1)
F
(F)) 皆為 L/K 的 intermediate fields,
利用 (1)
F ![]()
![]() (
(![]() (F)) 以及 Lemma 2.1.2 我們得到
(F)) 以及 Lemma 2.1.2 我們得到
![]() (
(![]() (
(![]() (F)))
(F))) ![]()
![]() (F). 然而
(F). 然而
![]() (F) 是
Gal(L/K) 的
subgroup, 故將 (1) 的 H 用
(F) 是
Gal(L/K) 的
subgroup, 故將 (1) 的 H 用
![]() (F) 取代, 可得
(F) 取代, 可得
![]() (F)
(F) ![]()
![]() (
(![]() (
(![]() (F))). 因此得證
(F))). 因此得證
![]() (F) =
(F) = ![]() (
(![]() (
(![]() (F))). 另一方面因為
H 和
(F))). 另一方面因為
H 和
![]() (
(![]() (H)) 皆為
Gal(L/K) 的 subgroups, 利用 (1)
H
(H)) 皆為
Gal(L/K) 的 subgroups, 利用 (1)
H ![]()
![]() (
(![]() (H)) 以及 Lemma 2.2.2 我們得到
(H)) 以及 Lemma 2.2.2 我們得到
![]() (
(![]() (
(![]() (H)))
(H))) ![]()
![]() (H). 然而
(H). 然而
![]() (H) 是 L/K 的
intermediate field, 故將 (1) 的 F 用
(H) 是 L/K 的
intermediate field, 故將 (1) 的 F 用
![]() (H) 取代, 可得
(H) 取代, 可得
![]() (H)
(H) ![]()
![]() (
(![]() (
(![]() (H))). 因此得證
(H))). 因此得證
![]() (H) =
(H) = ![]() (
(![]() (
(![]() (H))).
(H))). ![]()
![]() ) 只有兩個 subgroups: 即 {I} 和
Gal(L/
) 只有兩個 subgroups: 即 {I} 和
Gal(L/![]() ). 已知
). 已知
![]() ({I}) = L, 我們來探討
({I}) = L, 我們來探討
![]() (Gal(L/
(Gal(L/![]() )) 應該是哪一個 field.
由於
)) 應該是哪一個 field.
由於
![]() 都可唯一表示成
都可唯一表示成
![]() = r0 + r1
= r0 + r1![]() + r2
+ r2![]() + r3
+ r3![]() , 其中
r1, r2, r3, r4
, 其中
r1, r2, r3, r4 ![]()
![]() . 若
. 若
![]()
![]() L
L![]() , 我們有
, 我們有
![]() (
(![]() ) =
) = ![]() (F) = Gal(L/
(F) = Gal(L/![]() ) 以及
) 以及
![]() (L) = {I}. 因此我們有
(L) = {I}. 因此我們有
![]() (
(![]() ({I})) =
({I})) = ![]() (L) 且
(L) 且
![]() (
(![]() (Gal(L/
(Gal(L/![]() ))) =
))) = ![]() (F) 因此知
(F) 因此知
![]() )
) ![]()
![]() /2
/2![]() ×
×![]() /2
/2![]() 所以
Gal(L/
所以
Gal(L/![]() ) 共有 5
個 subgroups: {I},
Gal(L/
) 共有 5
個 subgroups: {I},
Gal(L/![]() ),
H1 = {I,
),
H1 = {I,![]() },
H2 = {I,
},
H2 = {I,![]() } 以及
H3 = {I,
} 以及
H3 = {I,![]() }. 我們先探討
}. 我們先探討
![]() 在這 5 個 subgroups 的取值. 首先我們已知
在這 5 個 subgroups 的取值. 首先我們已知
![]() ({I}) = L. 對於
({I}) = L. 對於
![]() (H1), 由於
(H1), 由於
![]() 的 intermediate fields 只有
的 intermediate fields 只有
![]() , F1,
F2, F3 以及 L, 因此知
, F1,
F2, F3 以及 L, 因此知
![]() :
: ![]() 和
和
![]() :
: ![]() 互為反函數, 也就是說
互為反函數, 也就是說
![]() 和
和
![]() 都是 1-1 且 onto. 這種 extension
就是所謂的 Galois Extension.
都是 1-1 且 onto. 這種 extension
就是所謂的 Galois Extension.