Galois Theory 雖然是針對 Galois extension, 不過在不是 Galois
extension 時也能應用. 最常見的情況是在 finite separable extension
時, 我們可以取 normal closure 而得到 Galois extension 再加以應用.
証 明.
因為
L/
K 是 finite extension, 存在
a1,...,
an  L
L 使得
L =
K(
a1,...,
an). 假設
ai over
K 的 minimal polynomial 為
pi(
x). 因為
L/
K 是 separable extension, 這些
pi(
x)
 K
K[
x]
皆為 separable polynomials. 若令
f (
x) =
p1(
x)
... pn(
x), 則由
normal closure 的定義知
N 為
f (
x) over
K 的 splitting field
且知
N/
K 是 finite normal extension (Proposition
3.2.9).
現假設
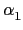 ,...,
,...,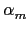
 N 為 f (x) 所有的根, 則
N = K(
N 為 f (x) 所有的根, 則
N = K(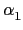 ,...,
,...,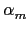 ). 然而每一個
). 然而每一個 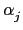 因為是
f (x) = p1(x) ... pn(x) 的一個根, 所以其 over K 的 minimal
polynomial 必為
p1(x),..., pn(x) 其中之一. 因此由
p1(x),..., pn(x) 皆為 separable polynomials 知
因為是
f (x) = p1(x) ... pn(x) 的一個根, 所以其 over K 的 minimal
polynomial 必為
p1(x),..., pn(x) 其中之一. 因此由
p1(x),..., pn(x) 皆為 separable polynomials 知
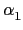 ,...,
,...,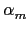 皆為 separable element over K. 故由
Theorem 3.4.7 知 N/K 是 separable extension. 因此 N/K 是
finite Galois extension.
皆為 separable element over K. 故由
Theorem 3.4.7 知 N/K 是 separable extension. 因此 N/K 是
finite Galois extension.
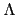
![]() ,...,
,...,![]()
![]() N 為 f (x) 所有的根, 則
N = K(
N 為 f (x) 所有的根, 則
N = K(![]() ,...,
,...,![]() ). 然而每一個
). 然而每一個 ![]() 因為是
f (x) = p1(x) ... pn(x) 的一個根, 所以其 over K 的 minimal
polynomial 必為
p1(x),..., pn(x) 其中之一. 因此由
p1(x),..., pn(x) 皆為 separable polynomials 知
因為是
f (x) = p1(x) ... pn(x) 的一個根, 所以其 over K 的 minimal
polynomial 必為
p1(x),..., pn(x) 其中之一. 因此由
p1(x),..., pn(x) 皆為 separable polynomials 知
![]() ,...,
,...,![]() 皆為 separable element over K. 故由
Theorem 3.4.7 知 N/K 是 separable extension. 因此 N/K 是
finite Galois extension.
皆為 separable element over K. 故由
Theorem 3.4.7 知 N/K 是 separable extension. 因此 N/K 是
finite Galois extension.
![]()