

下一頁: First Sylow's Theorem
上一頁: p-Group
前一頁: Conjugation as a group
在 abelian group 最好用的性質就是其每個 subgroup 都是 normal
subgroup, 所以每次碰到有關 abelian group 的性質時, 我們都可先找一個
nontrivial subgroup 再利用其為 normal 得到一個 order 比較小的
quotient group, 然後就可以用 induction. 在一般的 group
這方法就不再適用了, 因為可能並不存在 nontrivial normal subgroup
讓你做 quotient group. 接下來我們將證明 p-group 就有類似的好處,
除了個數是 p 的情況外 (這是 cyclic group
所以也不會造成麻煩), 其他的 p-group 都可找到一個 nontrivial
normal subgroup. 所以一些 p-group 的性質就可以用 induction 得到.
Theorem 4.3.1
若
G 是一個
p-group, 則
Z(
G)
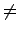
{
e}.
也就是說在
G
中存在一個元素
a e
e 且
a . g =
g . a,
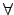 g
g  G
G.
証 明.
我們利用前面介紹的 conjugation 所造的 group action (
G,
S,*). 由於
|
G| = |
S|, 且因
G 是一個
p-group, 故得
| S| 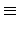 0(mod p). 0(mod p). |
(4.8) |
再因
G 是
p-group, 我們可以利用 Lemma
4.1.4 和式子
(
4.8) 得
|
S0|
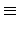
|
S|
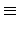
0(mod
p).
再加上式子 (
4.7) 我們知
|
S0| 是一個正整數且是
p 的倍數. 故由式子 (
4.6) 知
|
Z(
G)| = |
S0| > 1. 也因此得
Z(
G) 中存在著 identity 以外的元素,
故得證本定理.

Theorem 4.3.1 和前面談的 normal subgroup 有什麼關係呢? 其實
Z(G) 不只是 G 的 subgroup, 它是 G 的 normal subgroup. 因為若
a  Z(G), 則對任意的 g
Z(G), 則對任意的 g  G, 我們皆有
g . a . g-1 = a
G, 我們皆有
g . a . g-1 = a  Z(G). 所以 Z(G) 是 G 的 normal subgroup.
Z(G). 所以 Z(G) 是 G 的 normal subgroup.
証 明.
若
G 是 abelian, 從前已提過這時只有當 |
G| =
p 時才會是 simple
group. 所以由假設 |
G|
 p
p 知
G 不會是 simple group.
若 G 不是 abelian, 則
Z(G) 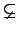 G 且由 Theorem
4.3.1 知
Z(G)
G 且由 Theorem
4.3.1 知
Z(G) {e}, 故知 Z(G) 是 G 的一個 nontrivial
proper normal subgroup. 所以 G 不是一個 simple group.
{e}, 故知 Z(G) 是 G 的一個 nontrivial
proper normal subgroup. 所以 G 不是一個 simple group.

我們已知最簡單的 p-group, 即 order 為 p 的 group 是 cyclic.
我們現在來探討 order 為 p2 的 group.
証 明.
如果
G 不是 abelian group 即表示
Z(
G)
 G
G, 再由 Theorem
4.3.1 知
Z(
G)

{
e}, 故由 Lagrange 定理 (Theorem
2.2.2) 知 |
Z(
G)| =
p. 現任取
a  G
G 但
a 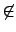 Z
Z(
G). 考慮
a 的 centralizer
C(
a) = {
g  G
G |
g . a =
a . g}.
由 Proposition
1.4.2 我們知
C(
a) 是
G 的一個 subgroup. 不過若
x  Z
Z(
G), 則
x . a =
a . x, 故知
x  C
C(
a). 也就是說
Z(
G)
 C
C(
a). 不過由假設
a 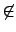 Z
Z(
G), 但
a 本身在
C(
a) 中 (因
a . a =
a . a), 故知
Z(
G)
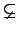 C
C(
a).
這告訴我們
|
C(
a)| > |
Z(
G)| =
p. 然而 Lagrange 定理告訴我們 |
C(
a)|
必須整除
p2, 因此得
|
C(
a)| =
p2. 由此推得
C(
a) =
G, 也就是所有
G 中的元素都在
C(
a). 換句話說所有
G 的元素都可和
a 交換.
這和我們當初假設
a 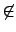 Z
Z(
G) 相矛盾. 所以知
G 一定是 abelian
group.

Proposition 4.3.3 並不能推廣到 | G| = pn, 其中 n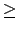 3 的狀況.
比方說將來我們將會看到存在 order 為 8 = 23 的 nonabelian group.
不過我們倒可以用前面所提的歸納法得到以下的結果:
3 的狀況.
比方說將來我們將會看到存在 order 為 8 = 23 的 nonabelian group.
不過我們倒可以用前面所提的歸納法得到以下的結果:
Proposition 4.3.4
若
G 是一個 group, 且 |
G| =
pn, 則
G 中存在一個 normal subgroup
N 其 order 為
pn - 1.
証 明.
我們用數學歸納法證明此定理. 當
n = 1 時 |
G| =
p, 而 {
e} 是
G
的 normal subgroup 且
|{
e}| =
p1 - 1 = 1. 故在此情形是成立的.
假設對於 | G| = pr, 且
1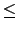 r
r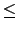 n - 1 時, 本定理也成立. 當
| G| = pn 時, 由 Theorem 4.3.1 知
Z(G)
n - 1 時, 本定理也成立. 當
| G| = pn 時, 由 Theorem 4.3.1 知
Z(G) {e}, 故由
Lagrange 定理知 Z(G) 也是一個 p-group. 因 p 整除 | Z(G)|,
故由 Cauchy 定理 (Theorem 4.2.1) 知存在一個 Z(G) 的
subgroup H 其 order 為 p. 因
H
{e}, 故由
Lagrange 定理知 Z(G) 也是一個 p-group. 因 p 整除 | Z(G)|,
故由 Cauchy 定理 (Theorem 4.2.1) 知存在一個 Z(G) 的
subgroup H 其 order 為 p. 因
H  Z(G), 故若 a
Z(G), 故若 a  H,
對於所有的 g
H,
對於所有的 g  G 皆有
a . g = g . a. 因此
g . a . g-1 = a . g . g-1 = a
G 皆有
a . g = g . a. 因此
g . a . g-1 = a . g . g-1 = a  H, 故知 H 是 G 的一個 normal
subgroup. 因 H 在 G 中 normal, 我們可考慮 G' = G/H 這個 quotient
group. 因
| G'| = | G|/| H| = pn - 1 我們可以用 induction 的假設知 G'
中存在一個 normal subgroup N' 其 order 為 pn - 2. 然而
Correspondence 定理 (Theorem 2.7.3) 告訴我們 G 中存在一個
normal subgroup N, 符合
H
H, 故知 H 是 G 的一個 normal
subgroup. 因 H 在 G 中 normal, 我們可考慮 G' = G/H 這個 quotient
group. 因
| G'| = | G|/| H| = pn - 1 我們可以用 induction 的假設知 G'
中存在一個 normal subgroup N' 其 order 為 pn - 2. 然而
Correspondence 定理 (Theorem 2.7.3) 告訴我們 G 中存在一個
normal subgroup N, 符合
H  N 且 N/H = N'. 也就是說
N 且 N/H = N'. 也就是說
| N| = | H| . | N'| = p . pn - 2 = pn - 1.
故完成本定理的証明.

Proposition 4.3.4 的結果當然比 Corollary 4.3.2 強,
它告訴我們當 | G| = pn 時我們可找到一個 G 的 normal subgroup
Gn - 1 其 order 為 pn - 1. 再對 Gn - 1 使用 Proposition
4.3.4 可得一個 Gn - 1 的 normal subgroup Gn - 2 其
order 為 pn - 2. 如此一直下去我們可得一串 G 的
subgroup:
{
e} =
G0 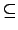 G1
G1 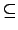 ...
... 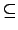 Gn - 1
Gn - 1 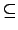 Gn
Gn =
G,
 G1
G1  ...
...  Gn - 1
Gn - 1  Gn = G, 其中 Gi 是
Gi + 1 的 normal subgroup, 且
Gi + 1/Gi 是一個 cyclic group,
則我們就說這個 group G 是一個 solvable group. Proposition
4.3.4 告訴我們一個 p-group 一定是一個 solvable group.
Gn = G, 其中 Gi 是
Gi + 1 的 normal subgroup, 且
Gi + 1/Gi 是一個 cyclic group,
則我們就說這個 group G 是一個 solvable group. Proposition
4.3.4 告訴我們一個 p-group 一定是一個 solvable group.


下一頁: First Sylow's Theorem
上一頁: p-Group
前一頁: Conjugation as a group
Administrator
2005-06-18
![]() Z(G), 則對任意的 g
Z(G), 則對任意的 g ![]() G, 我們皆有
g . a . g-1 = a
G, 我們皆有
g . a . g-1 = a ![]() Z(G). 所以 Z(G) 是 G 的 normal subgroup.
Z(G). 所以 Z(G) 是 G 的 normal subgroup.
![]() G 且由 Theorem
4.3.1 知
Z(G)
G 且由 Theorem
4.3.1 知
Z(G)![]() {e}, 故知 Z(G) 是 G 的一個 nontrivial
proper normal subgroup. 所以 G 不是一個 simple group.
{e}, 故知 Z(G) 是 G 的一個 nontrivial
proper normal subgroup. 所以 G 不是一個 simple group.
![]()
![]() 3 的狀況.
比方說將來我們將會看到存在 order 為 8 = 23 的 nonabelian group.
不過我們倒可以用前面所提的歸納法得到以下的結果:
3 的狀況.
比方說將來我們將會看到存在 order 為 8 = 23 的 nonabelian group.
不過我們倒可以用前面所提的歸納法得到以下的結果:
![]() r
r![]() n - 1 時, 本定理也成立. 當
| G| = pn 時, 由 Theorem 4.3.1 知
Z(G)
n - 1 時, 本定理也成立. 當
| G| = pn 時, 由 Theorem 4.3.1 知
Z(G)![]() {e}, 故由
Lagrange 定理知 Z(G) 也是一個 p-group. 因 p 整除 | Z(G)|,
故由 Cauchy 定理 (Theorem 4.2.1) 知存在一個 Z(G) 的
subgroup H 其 order 為 p. 因
H
{e}, 故由
Lagrange 定理知 Z(G) 也是一個 p-group. 因 p 整除 | Z(G)|,
故由 Cauchy 定理 (Theorem 4.2.1) 知存在一個 Z(G) 的
subgroup H 其 order 為 p. 因
H ![]() Z(G), 故若 a
Z(G), 故若 a ![]() H,
對於所有的 g
H,
對於所有的 g ![]() G 皆有
a . g = g . a. 因此
g . a . g-1 = a . g . g-1 = a
G 皆有
a . g = g . a. 因此
g . a . g-1 = a . g . g-1 = a ![]() H, 故知 H 是 G 的一個 normal
subgroup. 因 H 在 G 中 normal, 我們可考慮 G' = G/H 這個 quotient
group. 因
| G'| = | G|/| H| = pn - 1 我們可以用 induction 的假設知 G'
中存在一個 normal subgroup N' 其 order 為 pn - 2. 然而
Correspondence 定理 (Theorem 2.7.3) 告訴我們 G 中存在一個
normal subgroup N, 符合
H
H, 故知 H 是 G 的一個 normal
subgroup. 因 H 在 G 中 normal, 我們可考慮 G' = G/H 這個 quotient
group. 因
| G'| = | G|/| H| = pn - 1 我們可以用 induction 的假設知 G'
中存在一個 normal subgroup N' 其 order 為 pn - 2. 然而
Correspondence 定理 (Theorem 2.7.3) 告訴我們 G 中存在一個
normal subgroup N, 符合
H ![]() N 且 N/H = N'. 也就是說
N 且 N/H = N'. 也就是說