Abelian p-groups

大家都知道 cyclic group 一定是 abelian. 不過若只知ㄧ個 group 是 abelian 它並不一定會是 cyclic. 下一個 Lemma 告訴我們一個判斷 abelian group 是否為 cyclic 的方法.

証明. 若 | G| = pⁿ, 由 Lagrange 定理 (Corollary 2.3.4) 知 ord(a) = p^r, 其中 r 是一個正整數且 r $\le$ n.

(1) 若 G 是 cyclic, 即 G 中存在一元素 x 使得 G = $\langle$ x $\rangle$ . 也就是說 ord(x) = pⁿ. 然而已知 a 是 G 中元素 order 最大的之ㄧ. 所以知 ord(a) = pⁿ (注意這個元素並不唯一, 所以我們並不可得 x = a). 換句話說 G 和 $\langle$ a $\rangle$ 的元素個數一樣多, 即 G = $\langle$ a $\rangle$ .

(2) 若 G 不是 cyclic, 則當然 $\langle$ a $\rangle$ $\subsetneq$ G. 記 A = $\langle$ a $\rangle$ . 可知 quotient group G/A 仍是一個 abelian p-group, 即 | G/A| = p^{n - r}. 利用 Cauchy 定理 (Theorem 3.3.2) 知存在 $\overline{x}$ $\in$ G/A 使得 ord( $\overline{x}$ ) = p. 也就是說 $\overline{x}$ $\ne$ $\overline{e}$ 不過 $\overline{x}^{p}_{}$ = $\overline{e}$ , 因此 x $\not\in$ A 但 x^p $\in$ A. 因為 A = $\langle$ a $\rangle$ , x^p $\in$ A 表示存在一整數 i 使得 x^p = aⁱ. 我們用反證法證明 p | i.

如果 p $\nmid$ i, 則由 Proposition 2.3.3 知

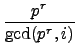ord(aⁱ) = $\displaystyle {\frac{p^r}{\gcd(p^r,i)}}$ = p^r.

也就是說 ord(x^p) = ord(a) = p^r. 別忘了 x $\in$ G, 而 G 是 p-group, 因此如前知 ord(x) = p^s, 其中 s 是一正整數. 再用一次 Proposition 2.3.3 知

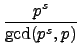ord(x^p) = $\displaystyle {\frac{p^s}{\gcd(p^s,p)}}$ = p^{s - 1}.

利用前面所求之 ord(x^p) = p^r 得 s = r + 1. 也就是說 ord(x) = p^s = p^{r + 1}. 別忘了當初我們假設 ord(a) = p^r. ord(x) > ord(a) 這和 a 的 order 是最大的相矛盾. 所以得證 p | i.

假設 i = pt, 令 b = a^{-t .}x. 注意若 b $\in$ A, 則因 x = a^{t .}b, 會導致 x $\in$ A, 這和 x $\not\in$ A 相矛盾, 故知 b $\not\in$ A, 且當然 b $\ne$ e (因 e $\in$ A). 然而因 G 是 abelian, b^p = a^{-pt .}x^p. 利用 pt = i 及 aⁱ = x^p, 我們推得 b^p = e. 由此可得 ord(b) = p. 這是因為由 Lemma 2.3.2 知 ord(b) | p. 但 p 是質數, 所以得 ord(b) = 1 or ord(b) = p. 然而已知 b $\ne$ e 即 ord(b) $\ne$ 1, 故可得 ord(b) = p. $\qedsymbol$

下一個 Lemma 告訴我們如果一個 abelian p-group 不是 cyclic 那麼它在某種程度上和 cyclic group 還是相差不遠.

証明. 令 A = $\langle$ a $\rangle$ . 若 G 不是 cyclic 則由 Lemma 3.3.8 知存在 b $\in$ G 但 b $\not\in$ A 使得 ord(b) = p. 令 B = $\langle$ b $\rangle$ . 首先證明 A $\cap$ B = {e}. 這是因為 A $\cap$ B 會是 B 的一個 subgroup. 利用 Lagrange 定理 (Theorem 2.2.2) 知 A $\cap$ B 的 order 需整除 B 的 order. 但 B 的 order 為質數 p, 故知 | A $\cap$ B| = 1 或 | A $\cap$ B| = p. 若 | A $\cap$ B| = p, 表示 A $\cap$ B = B, 即 B $\subseteq$ A. 這和 b $\not\in$ A 不合. 因此 A $\cap$ B 的 order 不是 p. 故得 | A $\cap$ B| = 1, 即 A $\cap$ B = {e}.

接下來我們想用 B 來幫我們以數學歸納法證明這個 Lemma. 若 G 的 order 為 p, 由 Corollary 2.2.3 知 G 是一個 cyclic group. 若 | G| = pⁿ. 假設此 Lemma 在所有 order 小於 pⁿ 的 abelian p-groups 都對.

當然若 G 是 cyclic 則證明完成, 但 G 是有可能不是 cyclic 的. 若 G 不是 cyclic, 考慮 G/B 這一個 abelian group. 因 | G/B| = p^{n - 1}, 故 G/B 是一個 order 小於 pⁿ 的 abelian p-group. 此時我們就可以用 induction 的假設, 不過要用這個假設我們得先在 G/B 中找到一個 order 最大的元素. 事實上 $\overline{a}$ 會是 G/B 中 order 最大的元素. 主要原因是由 Lemma 3.3.1 知對所有的 $\overline{x}$ $\in$ G/B, 都有 ord( $\overline{x}$ ) $\le$ ord(x). 又因 B $\cap$ $\langle$ a $\rangle$ = {e} 故再由 Lemma 3.3.1 得 ord( $\overline{a}$ ) = ord(a). 因為 a 是 G 中 order 最大的元素, 故得在 G/B 中對任意的 $\overline{x}$ $\in$ G/B 皆有

ord( $\displaystyle \overline{a}$ ) = ord(a) $\displaystyle \ge$ ord(x) $\displaystyle \ge$ ord( $\displaystyle \overline{x}$ ).

現在我們可以套用歸納的假設了. 由假設知有可能 G/B 是 cyclic, 要不然在 G/B 中存在一個 subgroup Q' 使得 G/B $\simeq$ $\langle$ $\overline{a}$ $\rangle$ ×Q'.

若 G/B 是 cyclic, 由 Lemma 3.3.8 知 G/B = $\langle$ $\overline{a}$ $\rangle$ . 此時我們要證明 G $\simeq$ $\langle$ a $\rangle$ ×B. 由 Theorem 3.2.4 知這相當於要證明 G = A^.B 且 A $\cap$ B = {e} (別忘了 A, B 都是 normal). 不過由於我們已證得 A $\cap$ B = {e}, 所以只要證 G = A^.B. 對任意的 x $\in$ G, 考慮 $\overline{x}$ $\in$ G/B. 則由於 G/B = $\langle$ $\overline{a}$ $\rangle$ , 故存在一整數 i 使得 $\overline{x}$ = $\overline{a}^{i}_{}$ . 這表示 x 和 aⁱ 在 B 的分類下是同類的. 也就是 (aⁱ)^{-1 .}x $\in$ B. 換句話說存在一整數 j 使得 x = a^{i .}b^j. 得證 G 中的元素都可寫成一個 A 中元素乘上一個 B 中元素的形式, 即 G = A^.B. 故加上 A $\cap$ B = {e} 得 G $\simeq$ A×B.

若 G/B 不是 cyclic 則由 induction 的假設知在 G/B 中存在一個 subgroup Q' 使得 G/B $\simeq$ $\langle$ $\overline{a}$ $\rangle$ ×Q'. 利用 Theorem 3.2.4 知此時 G/B = $\langle$ $\overline{a}$ $\rangle$ ^.Q' 且 $\langle$ $\overline{a}$ $\rangle$ $\cap$ Q' = { $\overline{e}$ }. 因為我們要把問題拉回到 G 來看, 利用 Correspondence 定理 (Corollary 2.7.3) 知在 G 中存在一個 subgroup Q 符合 B $\subseteq$ Q 且 Q/B = Q'. 我們要證明 G $\simeq$ $\langle$ a $\rangle$ ×Q.

首先證 G = A^.Q. 任取 x $\in$ G, 由於 $\overline{x}$ $\in$ G/B, 且 G/B = $\langle$ $\overline{a}$ $\rangle$ ^.Q/B, 故存在一整數 i 和 q $\in$ Q 使得

$\displaystyle \overline{x}$ = $\displaystyle \overline{a}^{i}_{}$ ^. $\displaystyle \overline{q}$ = $\displaystyle \overline{a^i\cdot q}$ .

也就是說 (a^{i .}q)^{-1 .}x $\in$ B. 因 B = $\langle$ b $\rangle$ , 由此知存在一整數 j 使得 (a^{i .}q)^{-1 .}x = b^j. 換句話說 x = a^{i .}(q^.b^j). 然而 aⁱ $\in$ A, 且 q^.b^j $\in$ Q (別忘了 B $\subseteq$ Q). 故知 G = A^.Q.

最後要證 A $\cap$ Q = {e}. 若 x $\in$ A $\cap$ Q, 由 x $\in$ A = $\langle$ a $\rangle$ 知存在一整數 i 使得 x = aⁱ. 故在 G/B 中 $\overline{x}$ = $\overline{a^i}$ = $\overline{a}^{i}_{}$ . 另一方面 a $\in$ Q 故在 G/B 中 $\overline{x}$ $\in$ Q/B = Q'. 也就是說

$\displaystyle \overline{x}$ $\displaystyle \in$ $\displaystyle \langle$ $\displaystyle \overline{a}$ $\displaystyle \rangle$ $\displaystyle \cap$ Q' = { $\displaystyle \overline{e}$ }.

由此知在 G/B 中 $\overline{x}$ = $\overline{e}$ , 也就是說 x $\in$ B. 但一開始已假設 x $\in$ A $\cap$ Q, 當然有 x $\in$ A. 所以得 x $\in$ A $\cap$ B. 別忘了我們已知 A $\cap$ B = {e}, 故得 x = e. 也就是說 A $\cap$ Q = {e}. $\qedsymbol$

Lemma 3.3.9 告訴我們什麼呢? 如果 G 是 abelian p-group, 且 | G| = pⁿ. 則有可能 G 是 cyclic group: 若是如此則由 Theorem 3.1.1 知 G $\simeq$ $\mathbb {Z}$ /pⁿ $\mathbb {Z}$ . G 也有可能不是 cyclic, 那麼 Lemma 3.3.9 就告訴我們若 G 中 order 最大的元素其 order 是 p^n₁, 則存在一個 subgroup Q 使得 G $\simeq$ ( $\mathbb {Z}$ /p^n₁ $\mathbb {Z}$ )×Q. 這裡因 G 是 abelian p-group, 其 subgroup Q 當然也是 abelian p-group. 如果 Q 是 cyclic, 那麼我們就可得 G $\simeq$ ( $\mathbb {Z}$ /p^n₁ $\mathbb {Z}$ )×Q $\simeq$ ( $\mathbb {Z}$ /p^n₁ $\mathbb {Z}$ )×( $\mathbb {Z}$ /p^n₂ $\mathbb {Z}$ ); 如果 Q 不是 cyclic 則再用一次 Lemma 3.3.9 知 Q 會 isomorphic to 一個 cyclic group 和 Q 的 subgroup 的 direct product. 這樣一直下去, 由於 G 的 order 是有限的經過有限次後一定會停. 我們可以有以下的結果: